Контрольные вопросы к лекции

1. Что является объектами схемотехнического проектирования?

2. Какие подходы используются при моделировании работы принципиальных электрических схем?

3. В чем состоит основная задача логического моделирования?

4. Какие существуют методы логического моделирования?

5. Для каких целей применяется синхронное логическое моделирование?

6. Для каких целей применяется асинхронное логическое моделирование?

7. В чем состоит различие между статическим и динамическим риском сбоя?

8. В чем состоит различие между двоичным и многозначным кодированием логических сигналов?

9. Какие основные физические законы лежат в основе моделирования логических схем?

10. Какие основные типовые задачи решаются при моделировании аналоговых схем?

11. В чем состоит различие между аппроксимацией и интерполяцией функциональных зависимостей?

12. Какие существуют методы моделирования статического режима?

13. В чем заключается сущность прямого метода моделирования?

14. В чем состоит суть метода установления?

15. В чем заключается метод движущейся области сходимости?

16. В чем состоит суть метода оптимизации?

17. В чем состоит суть моделирования в базисе узловых потенциалов?

18. Как формируется вектор узловых токов?

19. Как формируется матрица узловых токов?

20. Каким образом представляются идеальные источники тока и напряжения для моделирования в базисе узловых потенциалов?

Лекция №7

Моделирование переходных процессов. Моделирование частотных характеристик. Схемотехническое моделирование нелинейных и высокодобротных линейных радиочастотных схем. Расчет амплитуды установившегося режима высокочастотных колебаний во временной области. Расчет схем в частотной области в режиме малого сигнала. Расчет схем в частотной области в режиме большого сигнала. Статистический анализ. Метод расчета на наихудший случай. Метод статистических испытаний (Монте-Карло). Методы расчета и анализа выходных параметров схем. Одновариантный расчет. Многовариантный расчет. Анализ чувствительности. Методы анализа чувствительности.

7.1. Моделирование переходных процессов

Существует явная и неявная форма представления модели схемы для расчета переходных процессов.

Явная форма, в общем случае, состоит из двух подсистем:

1) , i=1,2,…n – обыкновенное дифференциальное уравнение (ОДУ) первого порядка,

2) конечное уравнение, где x – вектор переменных токов или напряжений для реактивных элементов, v – вектор постоянных и управляемых источников напряжения или тока, w – вектор переменных токов или напряжений для резистивных элементов.

Задача расчета переходного процесса по ОДУ сводится к решению задачи, известной в математике, как задача Коши. Она заключается в поиске функции x(t), удовлетворяющей заданному начальному условию x(t₀)=x₀ на конечном интервале . Численно эта функция определяется в отдельных точках (узлах) интервала t₁,t₂...t_n в виде таблицы t₁,t₂...t_n , с соответствующими приближенными значениями x(t₁), x(t₂)…x(t_n) точного решения x(t). Расстояние между узлами называется шагом интегрирования – h. Значения функции в соседних узлах связаны между собой соотношением . Наиболее широко для решения ОДУ используется метод Эйлера: _.

Пример модели диодно-резисторной схемы в явном виде

Так как , то ОДУ, описывающее работу схемы, имеет вид: ).

Соответствующая система конечных уравнений имеет вид:

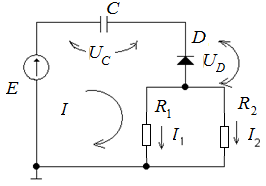
Рис. 7.1. Пример диодно-резисторной схемы

Неявная форма в общем случае имеет вид: , где i=1,2…p. Для решения данной задачи используется замена производных и интегралов аппроксимирующими выражениями. Такой прием называется дискретизацией и алгебраизацией математической модели. Именно дискретизация и алгебраизация составляют сущность построения динамической модели (модели для исследования переходных процессов) в неявной форме.

При моделировании переходных процессов также используется базис узловых потенциалов с автоматическим выбором шага . В результате модель для исследования переходных процессов практически не отличается от модели для статического режима. Просто переходный процесс рассматривается как совокупность (последовательность) различных статических режимов схемы, что значительно упрощает программу схемотехнического моделирования.