4.4. Способы формирования случайных величин
В основе рассмотренных типовых задач структурного моделирования лежит процесс генерации случайных величин. В связи с этим практический интерес представляют способы генерации случайных чисел.
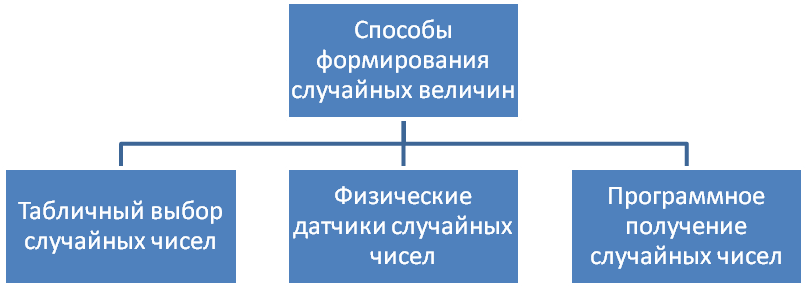
Рис.4.11. Способы генерации случайных величин
1). Таблицы случайных чисел представляют собой последовательности (a1,a2…an) из цифр 0,1…9, имеющих равную вероятность появления (например, при бросании кости, вращения рулетки и т.п.). Если нужна случайная цифра N, то берется любое число из таблицы. Если требуется число x, то из таблицы берут n очередных цифр. Например, x=a1,a2,a3 или x=a4,a5,a6 для трехзначного числа. Цифры можно брать подряд с любого места в любом направлении.
2). Физические датчики, например, диоды, транзистора и т.п. Случайное напряжение U с генератора поступает на компаратор, на выходе которого формируется логическая 1 при превышении порога U0 или логический 0, если U < U0. В момент действия тактовых импульсов результат считывается и на выходе получается последовательность случайных 0 и 1, из которых можно составить числа любой разрядности.
3). Программы получения случайных чисел формируют случайное число из предыдущего в результате некоторых функциональных преобразований 𝜁n+1=F(𝜁n). Такие числа называются псевдослучайными, т.к. их формируют алгоритмы, случайностей не допускающие. Однако, псевдослучайные числа могут вполне в ряде задач заменить настоящие случайные числа. Существуют специальные тесты проверки псевдослучайных чисел, например, тест соответствия принятому закону распределению, тест серий, проверяющий независимость следующих друг за другом групп чисел, тест интервалов, проверяющий частоту появления одинаковых чисел и др.
Рис.4.12. Схема и временные диаграммы работы датчика случайной величины
4.4.1. Моделирование равномерного распределения
Наиболее часто для генерации равномерного распределения псевдослучайных чисел применяется формула вида 𝜁n+1=K𝜁nmodM. , где 𝜁i – целые числа, K – специально подобранное большое целое число, а операция умножения K𝜁n производится по модулю M. Таким образом, если K𝜁n≥М, то в качестве 𝜁n+1 берется остаток от деления K𝜁n /М. Графически эта функция представляет собой множество прямых линий в квадрате со стороной М. Псевдослучайные числа 𝜁i располагаются на наклонных линиях. Настоящие случайные числа покрывают весь квадрат М×М. Дополнив рассмотренную процедуру преобразованием вида 𝜁*n+1 =𝜁n+1 /М , получим случайные числа, равномерно распределенные на интервале [0,1], которые являются базовыми для формирования случайных чисел с произвольным законом распределения.
Пример: При К=12, 𝜁n=3, М=7 генерируется последовательность псевдослучайных чисел 3,1,5,4,6.... Действительно, для K𝜁n/М=12×3/7 остаток 1=𝜁n+1, далее для 12х1/7 остаток 5=𝜁n+2, для 12×5/7 остаток 4=𝜁n+3, для 12×4/7 остаток 6=𝜁n+4 и т. д.
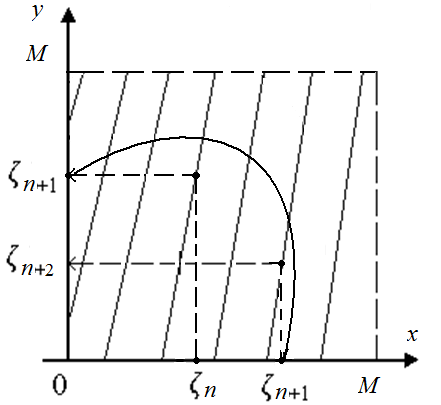
Рис. 4.4.13. Графическая иллюстрация процесса получения равномерно распределенных случайных чисел