Идентификация объекта регулирования с использованием векторно-матричного описания

Конечно-разностное уравнений может быть представлено в векторно-матричном виде следующим образом:

(1.1)

где

Критерий метода наименьших квадратов в векторно-матричном виде запишется:

, где (1.2).

Вектор экспериментальных значений выхода размерности n₀ примет вид: . Вектор, рассчитанных по модели значений выхода объекта, размерностью n₀ :

С учетом выражения (1.1) вектор y может быть представлен следующим выражением:

(1.3)

где матрица вида

=

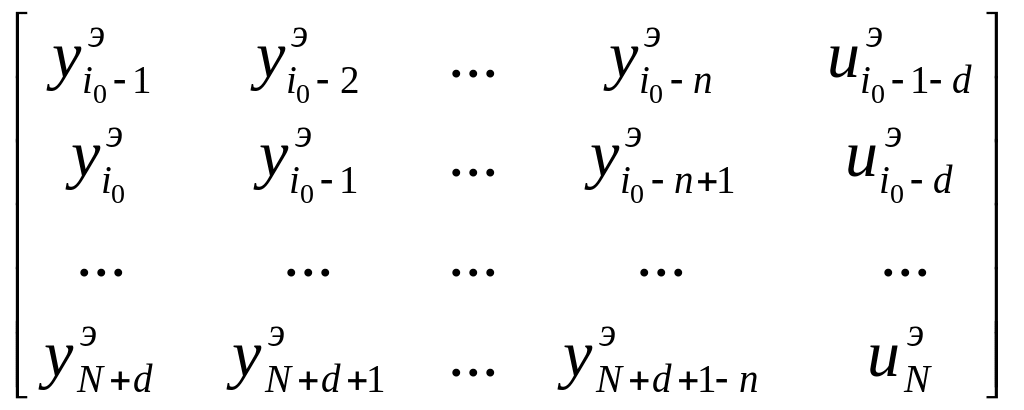
Это матрица экспериментальных значений входа и выхода. Каждая из строк которой предназначена для расчета по модели соответствующего выхода объекта. С учетом выражения (1.3) критерий метода наименьших квадратов примет следующий вид:

(1.4)

Система линейных уравнений, полученная путем дифференцирования критерия Ф по параметрам конечно-разностного уравнения примет вид:

(1.5.а)

где или (1.5.b)

Выполняя преобразование выражений (1.5.а) и (1.5.b) можно представить их в виде:

(1.6.а)

(1.6.b)

Выражая из (1.6.а) и (1.6.б) вектор параметров конечно-разностных уравнений получим:

(1.7a)

(1.7b)

Как видно из формул расчета вектор оценок искомых параметров модели (1.7.а), (1.7.б) необходимым условием является обратимость матрицы . Из вида матрицы , имеющей размерность следует, что ее ранг не может превышать наименьшую размерность, т.е.

Если количество измерений N₀ меньше количества искомых параметров (n+1), то ранг матрицы будет равен: , тогда по известному свойству ранг произведения не будет превышать количества измерений N₀.

. На основе этого равенства следует, что определитель матрицы , поскольку размерность . В этом случае система уравнений (1.5.а), (1.5.b) может быть либо несовместимой (т.е. не имеет решения), либо не определенной (имеет бесконечное множество решений). Вне зависимости от результата из полученного следует, что оценка параметров конечно-разностного уравнения не может быть найдена. Таким образом, при идентификации экспериментальных значений должно быть больше количества определяемых параметров КРУ.

Получение конечно-разностных уравнений цифровых регуляторов и области допустимых изменений параметров.

Цифровой регулятор в общем виде может быть представлен конечно-разностным уравнением m-го порядка.

Структурная схема регулятора:

,

где выход регулятора (регулирующее воздействие),

ошибка регулирования сигнала рассогласования,

настроечные параметры цифрового регулятора,

порядок цифрового регулятора.

Ошибка регулирования определяется следующим выражением: ,

где задающее воздействие,

текущее значение регулируемой величины.

Подставляя правую часть в уравнение регулятора получим: .

Получим конечно-разностное уравнение цифрового регулятора из дифференциального уравнения ПИД-регулятора:

где коэффициент усиления,

время изодрома,

время предварения.

Продифференцируем обе части уравнения, получим:

Заменим производные конечно-разностным уравнением, получим:

. Выразим

: .

Понизим индекс на единицу:

Полученное уравнение называется конечно-разностным уравнением цифрового регулятора второго порядка, где настроечные параметры. Полученное уравнение позволяет выполнить следующее:

1. параметры цифрового регулятора можно вычислить по настройкам , что позволяет реализовать аналоговый регулятор с помощью цифровой вычислительной техники

2. из уравнения взаимосвязи настроек цифрового и аналогового регуляторов видно, что они равны по количеству, т.е. настройка цифрового равна настройке аналогового регулятора

3. из уравнения взаимосвязи видно, что размерность настроек цифрового регулятора совпадает с размерностью настроек аналогового регулятора

Для получения конечно-разностного уравнения ПИ регулятора необходимо постоянную дифференцирования приравнять к нулю. Дифференциальное уравнение ПИ-регулятора:

Цифровые настройки будут равны: , ,

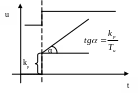
Следовательно цифровой ПИ-регулятор примет вид: . Построим график переходного процесса для регулятора первого порядка (цифровой ПИ-регулятор) при подаче на его вход единичного ступенчатого воздействия. Для этого укажем ограничения для , необходимые для реализации ПИ-закона в цифровом виде:

1. или

2. или для ПИ-регулятора

3. при условии, что

Расчет переходного процесса по конечно-разностным уравнениям должен выполнятся на основе начальных условий, которые примут вид:

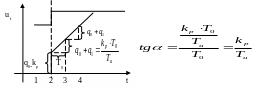
Построим переходной процесс для ПИД-закона в цифровом виде. Для этого запишем ограничения на настройки цифрового регулятора, обеспечивающие реализацию ПИД закона. При этом .

1.

2.

3.

4.

5.

6.

7.

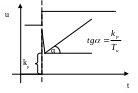
Для расчета переходного процесса цифрового ПИД-регулятора зададим начальные условия:

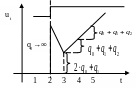
Цифровой регулятор, описывающийся конечно-разностным уравнением, охватывает больший класс законов регулирования, чем аналоговый. При выполнении ограничений на настройки цифрового регулятора они реализуют аналоговые законы. В противном случае – чисто цифровые законы регулирования.

Внимание! При выводе конечно-разностных уравнений цифровых регуляторов дифференцируют обе части уравнений аналогового регулятора только в том случае, когда есть интегрирующая составляющая.

Для регулятора, описываемого конечно-разностным уравнением m-го порядка, в общем случае . Начальные условия для расчета переходного процесса будут иметь вид: