Аппроксимация переходных процессов.

Динамической моделью объекта, описывающей его динамические свойства, т.е. изменения выхода объекта в переходном режиме из одного установившегося состояния в другое с учетом времени называется математическая зависимость вида:

Однако, на практике записать данную математическую зависимость в представленном виде зачастую сразу невозможно, проще бывает сначала записать дифференциальное уравнение, описывающее динамические свойства объекта, а затем, решив его, получить искомую функцию. При этом данное дифференциальное уравнение называют динамической моделью. При проведении анализа динамических свойств объекта ОР и синтеза систем регулирования с использованием ЭВМ применение дифференциальных уравнений исключается, т.к. основными математическими операциями любого языка программирования является +,-,×,/. Поэтому возникает задача представления динамической модели объекта или системы в виде выражения включающего только указанные операции. Рассмотрим получение данной модели. В общем случае динамические свойства любого линейного ОР могут быть описаны дифференциальным уравнением n-го порядка.

где - коэффициенты дифференциального уравнения

k- коэффициент усиления

- время чистого запаздывания

n- порядок дифференциального уравнения

По определению производная есть:

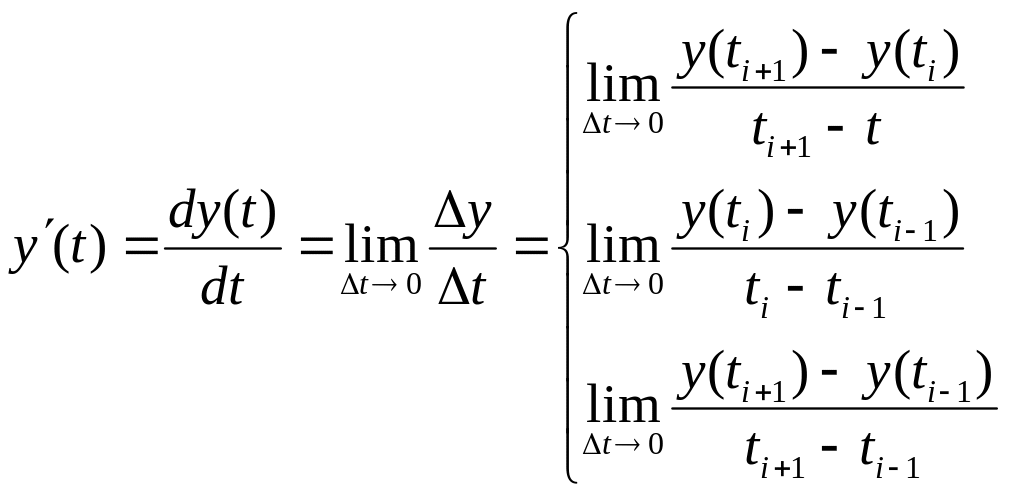
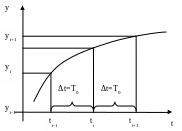
Отбрасывая знак предела можно получить приближенные формулы расчета производной. Обозначим:

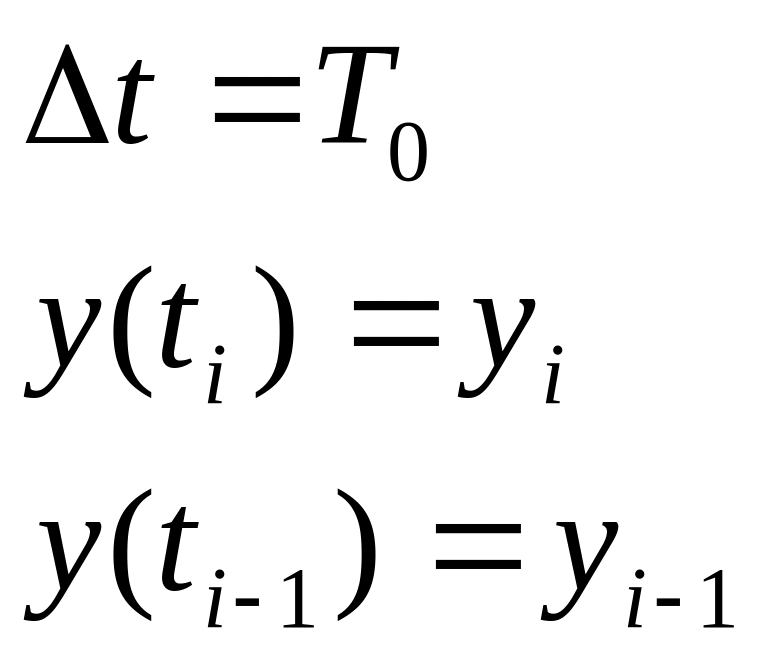
Получим приближенные формулы расчета производной:

-правое, левое и центральное КРО первого порядка

Получая для второй, третьей и т.д. n-ой производных конечно-разностные отношения и подставляя их в исходное дифференциальное уравнение вместо соответствующих производных, приводя подобные и выражая можно получить конечно-разностное уравнение являющееся дискретной динамической моделью удовлетворяющей указанным выше требованиям.

Замена производных конечно-разностными отношениями

1.

Первую производную заменяем правым конечно-разностным отношением.

2.

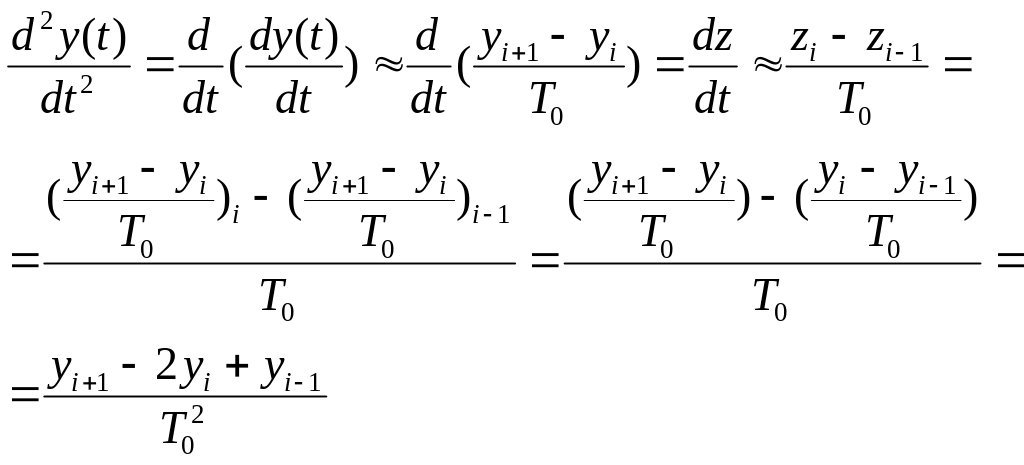
Используя полученные КРО для первой и второй производных, рассмотрим вывод КРУ на примере дифура второго порядка:

Для перехода заменим производные соответствующими конечно-разностными отношениями, саму функцию y(t) заменим как :

Сгруппируем подобные слагаемые с соответствующим y:

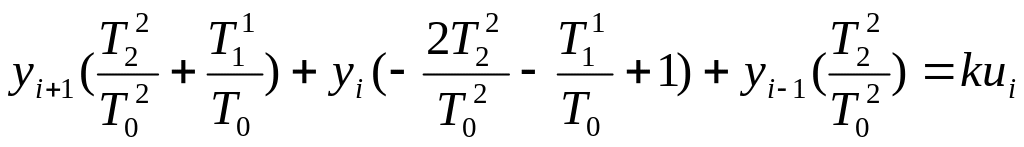
В скобках приведем к общему знаменателю:

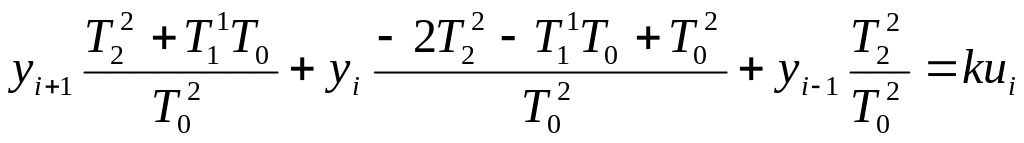
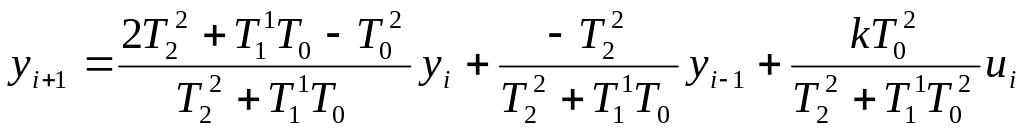
Обозначим: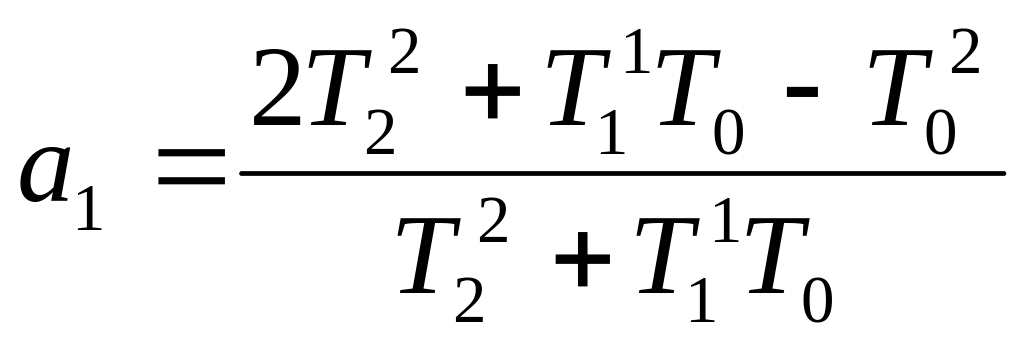

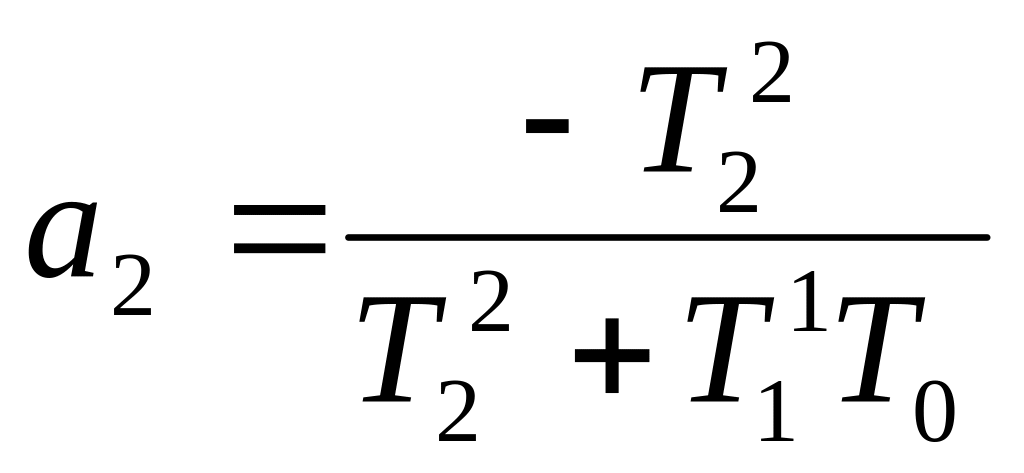
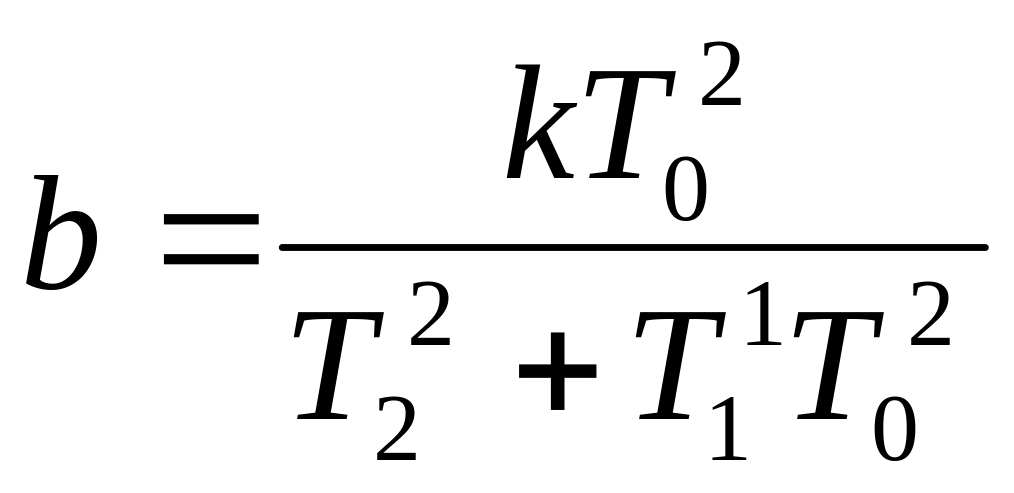
Индекс у всех слагаемых понижаем на единицу, получаем:

- это конечно-разностное уравнение второго порядка без запаздывания.

При наличии запаздывания дифференциальное уравнение примет вид:

где - время чистого запаздывания.

Вывод конечно-разностного уравнения в этом случае будет аналогичен рассматриваемому выше, с той разницей, что у входа u индекс будет иметь вид (i-1-d),где -целое число тактов запаздывания. Тогда конечно-разностное уравнение примет вид:

- это конечно-разностное уравнение второго порядка с запаздыванием.

Представленные конечно-разностные уравнения второго порядка с запаздыванием и без запаздывания являются дискретными динамическими моделями ОР и позволяют найти численное решение соответствующего дифференциального уравнения (т.е. временную характеристику) при известных коэффициентах дифференциального уравнения , времени чистого запаздывания и известном законе изменения входа . Полученное выражение для коэффициентов называется формулой взаимосвязи коэффициентов дифференциального и соответствующего конечно-разностного уравнения. При известных коэффициента дифференциального уравнения и такте квантования Т₀, можно определить коэффициенты , и наоборот.

При наличии конечно-разностных уравнений и известных параметрах можно осуществить расчет динамической характеристики объекта, т.е. найти и построить любую временную характеристику. Для этого необходимо знать закон изменения входа (закон изменения управляющего воздействия u(t) и начальные условия). Начальные условия – это значение входа и выхода объекта перед подачей управляющего воздействия. Для дифференциального уравнения второго порядка без запаздывания, которому соответствует конечно-разностное уравнение вида: при построении кривой разгона начальные условия примут вид:

Тогда выход ОУ (численное решение дифференциального уравнения, являющегося переходной функцией), при единичном ступенчатом воздействии будет получено следующим образом:

В итоге получим численное решение дифференциального уравнения второго порядка – переходную функцию h(t).

Для дифференциального уравнения n-го порядка конечно-разностное уравнение примет вид:

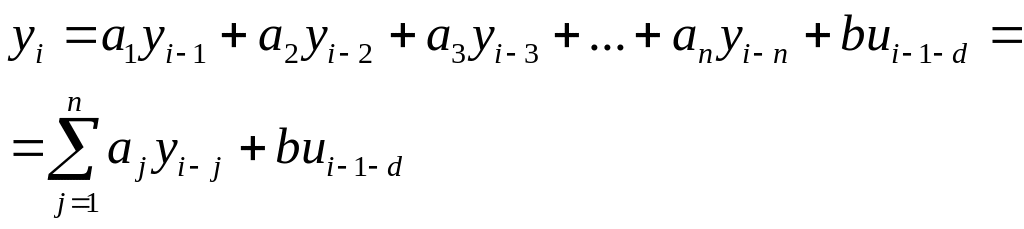
где n- порядок дифференциального уравнения и соответствующего ему конечно-разностного.

Начальные условия в этом случае примут вид:

для входа

для выхода

где , N- определенное количество рассчитанных точек переходного процесса.

Расчет переходных процессов по дискретной динамической модели в виде конечно-разностного уравнения осуществляется в приращениях. Под приращением подразумевается следующее:

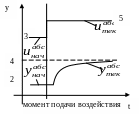
Конечно-разностные уравнения описывают больший класс динамических звеньев, чем аналогичные модели. Чтобы конечно-разностные уравнения описывали широко известные звенья (например, апериодическое первого, второго порядка, консервативное и т.д.) необходимо, чтобы выполнялся ряд ограничений на параметры , например для конечно-разностного уравнения второго порядка, чтобы оно описывало апериодическое звено, необходимо, чтобы коэффициент или в зависимости от знака коэффициента усиления к.