
- •Цель курса
- •Основные понятия и определения
- •Классификация систем управления
- •Характеристики технических средств автоматизации.
- •Разработка математической дискретной модели объекта.
- •Синтез математической модели с использованием экспериментально-статистического подхода (идентификация объекта управления).
- •Снятие временных характеристик
- •Аппроксимация переходных процессов.
- •Параметрическая идентификация дискретной динамической модели методом наименьших квадратов
- •Идентификация объекта регулирования с использованием векторно-матричного описания
- •Получение конечно-разностных уравнений цифровых регуляторов и области допустимых изменений параметров.
- •Расчет переходного процесса замкнутой цср по задающему и возмущающему воздействию.
- •Рассмотрим расчет переходного процесса замкнутой цср при подаче возмущающего воздействия на вход ор в виде единичного импульса.
- •Алгоритм оптимизации настроек цифрового регулятора
- •Укрупнённая схема алгоритма поиска оптимальных настроек цр в одноконтурной системе.
- •Использование оператора сдвига z для описания дискретных систем
- •Синтез многоконтурных цср
- •Синтез каскадной системы регулирования
- •Укрупненная схема алгоритма оптимизации по критерию время регулирования настроек внешнего регулятора
- •Синтез комбинированных цср
- •Многосвязные системы регулирования
- •Системы несвязного регулирования
- •Синтез системы связного регулирования
Синтез каскадной системы регулирования
Синтез каскадной системы регулирования включает в себя стандартные этапы:
разработка математической модели внутреннего и внешнего объекта путем идентификации на основе использования метода наименьших квадратов
расчет управляющей части (внутреннего и внешнего регулятора)
Идентификация объекта осуществляется следующим образом: на вход объекта, находящемся в установившемся состоянии подается входное воздействие и осуществляется измерение вспомогательных и основных технологических величин, как показано на структурной схеме:
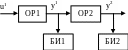
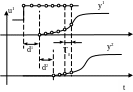
Далее полученные кривые разгона разбиваются одним и тем же тактом квантования, начиная с момента подачи ступенчатого воздействия. На основе полученных экспериментальных данных, осуществляют расчет параметров моделей внутреннего и внешнего объекта.
![]() рассчитывает
модель внутреннего объекта
рассчитывает
модель внутреннего объекта
![]()
![]() рассчитывает
модель внешнего объекта
рассчитывает
модель внешнего объекта![]()
При этом модель внутреннего и внешнего объекта может быть записана:
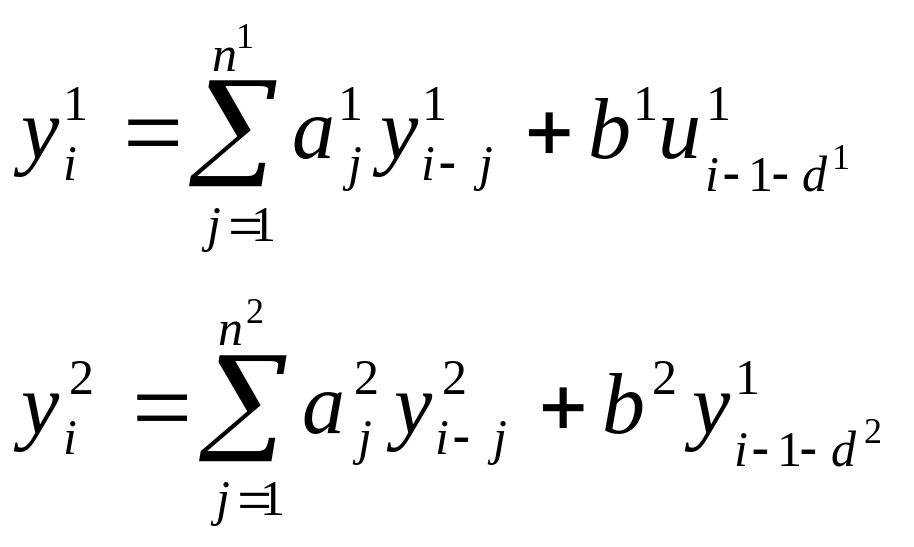
Расчет управляющей части комбинированной системы регулирования может осуществляться с использованием двух подходов:
сначала рассчитывается внутренний регулятор, затем внешний
сначала рассчитывается внешний регулятор, затем внутренний
Рассмотрим расчет управляющей части по первому подходу. Вначале рассчитаем внутренний регулятор по алгоритму одноконтурной системы:

Выделяем внутренний контур:

Далее рассчитаем внешний регулятор, при этом могут быть использованы два метода:
метод декомпозиции
метод свертки
Метод декомпозиции заключается в том, что при настройке внешнего регулятора используется описание каждого из элементов каскадной системы (внутренние и внешние регуляторы, внутренние и внешние объекты) при этом описание каскадной системы с использованием конечно-разностного уравнения примет вид:
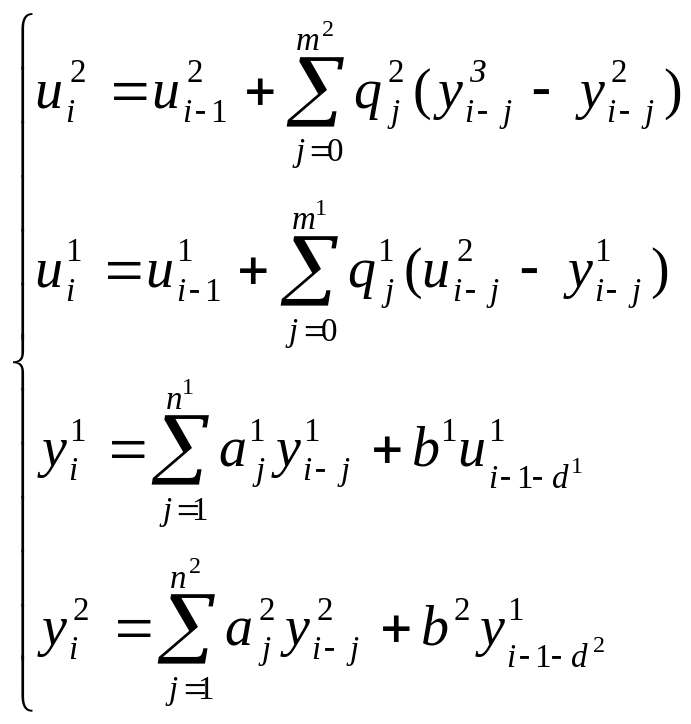
где
![]() известные параметры внутреннего и
внешнего объекта и регулятора
известные параметры внутреннего и
внешнего объекта и регулятора
![]() неизвестные
оптимизирующие настройки внешнего
регулятора
неизвестные
оптимизирующие настройки внешнего
регулятора
Рассмотрим настройки
внешнего регулятора на примере критерия
интегрально-квадратичной ошибки:
![]() .
В этом случае алгоритм оптимизации
внешнего регулятора включает те же
этапы, что и алгоритм оптимизации
регулятора в одноконтурной системе.
Отличие в том, что в расчете частных
производных критерия по настройке
внешнего регулятора:
.
В этом случае алгоритм оптимизации
внешнего регулятора включает те же
этапы, что и алгоритм оптимизации
регулятора в одноконтурной системе.
Отличие в том, что в расчете частных
производных критерия по настройке
внешнего регулятора:
![]()
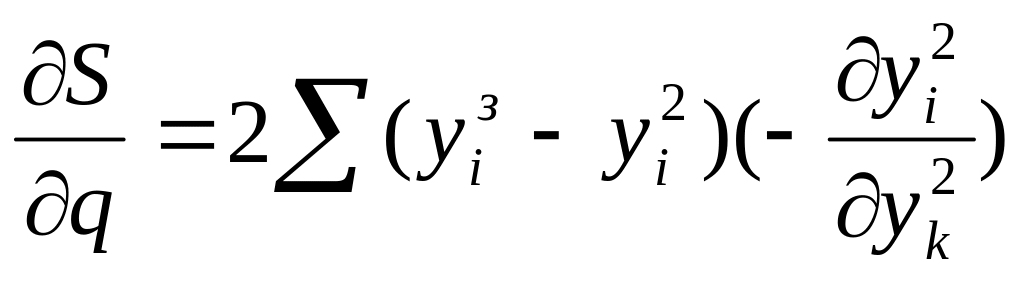
Для расчета следующего приближения к точке экстремума необходимо знать частные производные по настройкам внешнего регулятора, отсюда вытекает необходимость дифференциального уравнения регуляторов и объектов по настройкам внешнего регулятора:
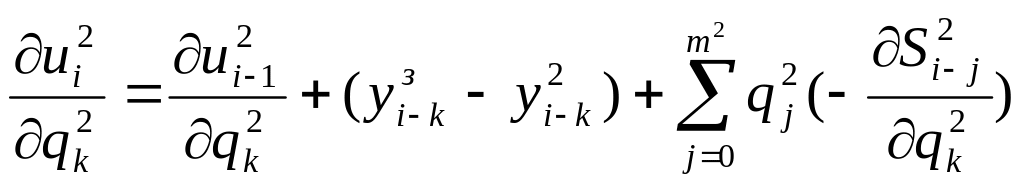
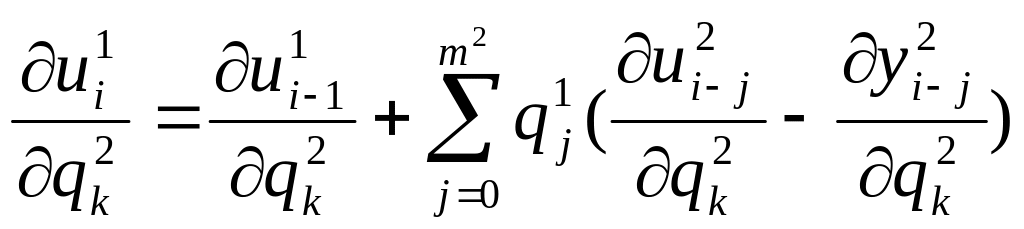

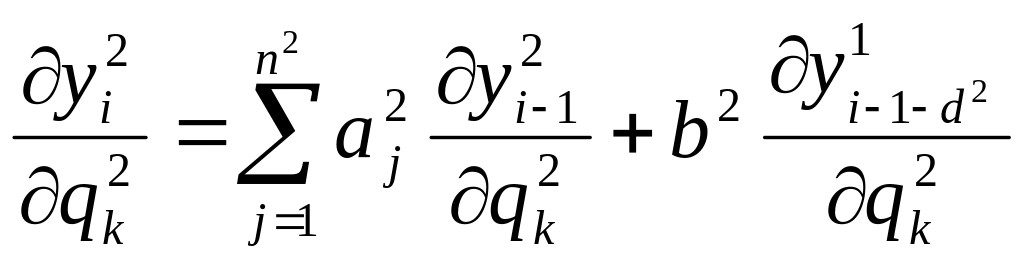
Используя записанные
системы уравнений для расчетов выходов
регуляторов и объектов, а также их
частных производных осуществляется
оптимизация настоек внешнего регулятора.
При этом укрупненная схема алгоритма
принимает такой же вид, как при оптимизации
регулятора в одноконтурной системе
регулирования. Рассмотрим вариант
оптимизации внешнего регулятора
каскадной системы на основе метода
декомпозиции по критерию время
регулирования
![]() .
Оптимизация настроек внешнего регулятора
.
Оптимизация настроек внешнего регулятора
![]() осуществляется аналогично одноконтурной
системе при использовании численного
метода оптимизации (метод градиента).
Расчет оптимальных настроек будет
осуществляться по приведенному выше
уравнению.
осуществляется аналогично одноконтурной
системе при использовании численного
метода оптимизации (метод градиента).
Расчет оптимальных настроек будет
осуществляться по приведенному выше
уравнению.
![]()
Главным отличием
в этом случае от предыдущего варианта
является невозможность использования
квазианалитических рекуррентных
зависимостей для расчетов частных
производных критерия по оптимизируемым
настройкам, т.к. критерий явно не зависит
от выхода системы
![]() .
.
![]()
![]()
Для расчета частных производных критерия поступим следующим образом:
на каждой итерации производится расчет переходного процесса по уравнениям описывающим каскадную систему регулирования при известных параметрах
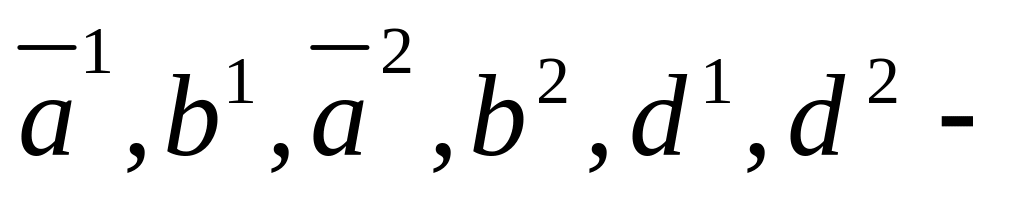 и известных настройках внутреннего
регулятора
и известных настройках внутреннего
регулятора
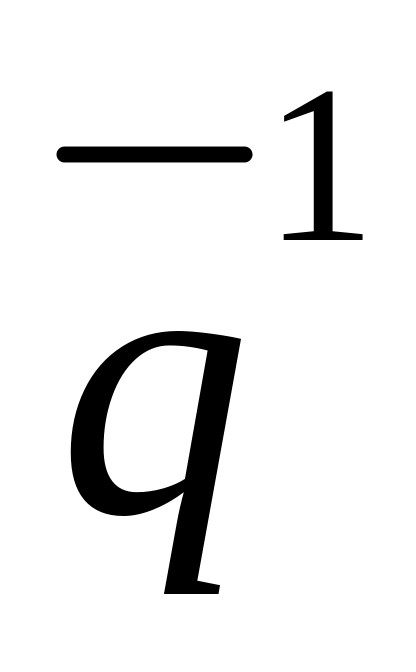 и заданном (известном) текущем приближении
к оптимальным настройкам внешнего
регулятора
и заданном (известном) текущем приближении
к оптимальным настройкам внешнего
регулятора
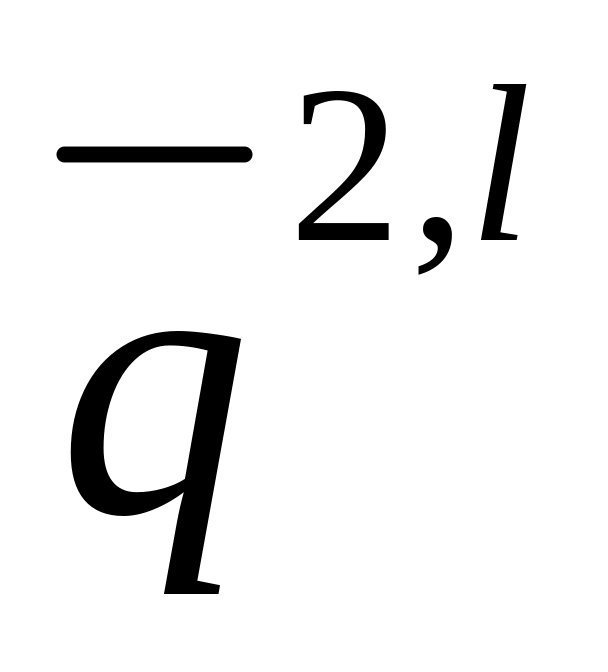 ,
номер
итерации.
,
номер
итерации.затем рассчитывается значение критерия (время регулирования в данном случае)
затем первая настройка внешнего регулятора изменяется на малую величину
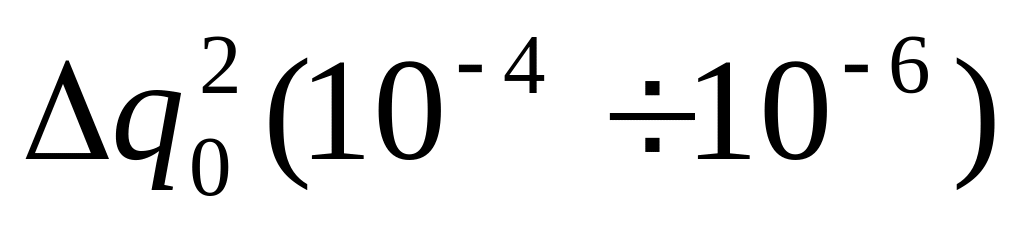 .
Остальные настройки внешнего регулятора
остаются прежними и снова выполняется
расчет переходного процесса по системе
конечно-разностного уравнения каскадной
системы и расчет значения критерия
(время регулирования). Тогда частная
производная критерия по настройке
.
Остальные настройки внешнего регулятора
остаются прежними и снова выполняется
расчет переходного процесса по системе
конечно-разностного уравнения каскадной
системы и расчет значения критерия
(время регулирования). Тогда частная
производная критерия по настройке
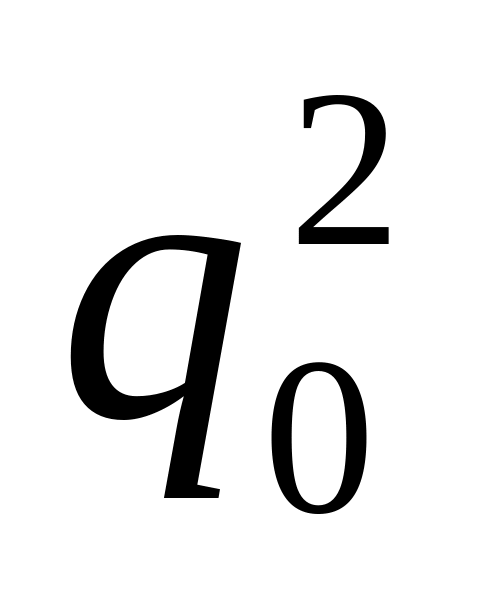 будет рассчитана по зависимости:
будет рассчитана по зависимости:
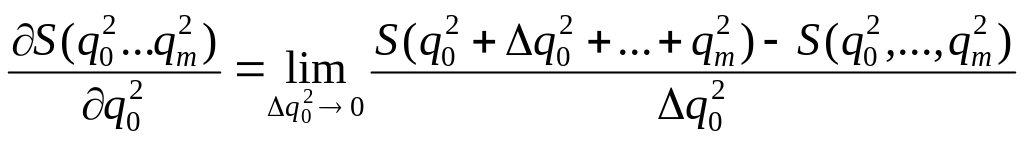
4. После этого
делают приращение настройки к
![]() в виде
в виде
![]() оставляя прежними остальные настройки
регулятора и рассчитывается переходной
процесс, а также соответствующему ему
значения критерия. Тогда частная
производная по настройке
будет рассчитана:
оставляя прежними остальные настройки
регулятора и рассчитывается переходной
процесс, а также соответствующему ему
значения критерия. Тогда частная
производная по настройке
будет рассчитана:
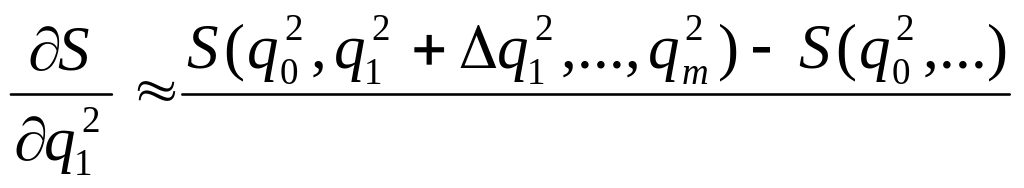
Частная производная по k-ой настройке l-ой итерации будет рассчитываться:
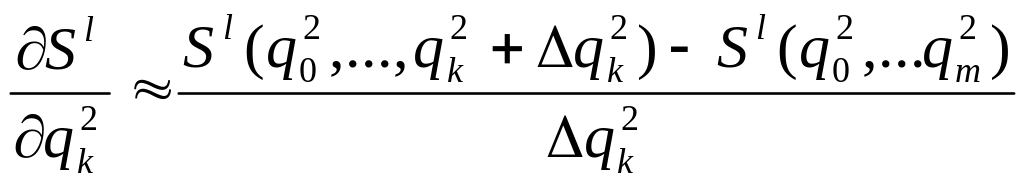
5. После расчета частной производной критерия выполняется расчет следующего приближения к точке минимума по настройке внешнего регулятора
6. На следующей итерации все перечисленные действия повторяются. Для расчета переходного процесса по заданию необходимо задать начальные условия:
![]()
![]()
![]()
![]()
![]()
