- •4.1. Основные понятия и определения
- •4.2. Законы Кирхгофа и Ома в комплексной форме
- •4.5. Метод комплексных амплитуд (символический метод)
- •4.9. Методы анализа (расчета) линейных цепей при гармоническом воздействии
- •В ариант № 6–6.
- •В ариант № 6–8.
- •В ариант № 6–9.
- •В ариант № 6–23.
- •Вариант № 6–24.
Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
Казанский Государственный Технический Университет
им. А.Н. Туполева
_____________________________________________________________
Кафедра радиоэлектроники и информационно-измерительной техники
задания и методические указания по расчету цепей гармонического тока
(методические указания для студентов-заочников)
Авторсоставитель: Погодин Д.В.,
Казань - 2010 г.
4.1. Основные понятия и определения
Синусоидальными сигналами или воздействиями называются переменные напряжения и токи источников, которые аналитически можно записать с помощью синусоидальной функции в синусной или косинусной форме:
![]() ,
,
![]() .
.
Рис. 4.1. Временная диаграмма синусоидального напряжения |
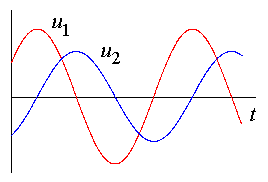
Рис. 4.2. Напряжение u1 опережает напряжение u2 |
Как
правило, в теории электрических цепей
синусоидальные функции напряжений и
токов записывают в косинусной форме,
поскольку косинус функция четная и с
ней проще оперировать. В записанных
выражениях Um
и Im
амплитудные
значения напряжения и тока,
![]()
фаза колебаний,
фаза колебаний,
![]()
угловая частота или скорость изменения
фазы (измеряется в радианах в секунду),
угловая частота или скорость изменения
фазы (измеряется в радианах в секунду),
![]() и
и
![]()
начальные фазы колебаний (измеряются,
как правило, в пределах от
начальные фазы колебаний (измеряются,
как правило, в пределах от
![]() до
до
![]() ).
).
![]()
циклическая частота, измеряется в
герцах. Временная диаграмма (график)
переменного синусоидального напряжения
представлена на рис. 4.1.
циклическая частота, измеряется в
герцах. Временная диаграмма (график)
переменного синусоидального напряжения
представлена на рис. 4.1.
При
наличии двух или нескольких сигналов
между ними может существовать сдвиг
фаз
![]() .
Если угол
.
Если угол
![]() ,
то напряжение
,
то напряжение
![]() опережает
опережает
![]() на
угол
на
угол
![]() ,
как это показано на рис. 4.2.
,
как это показано на рис. 4.2.
Рис. 4.3. Напряжения совпадают по фазе |
Рис. 4.4. Напряжения находятся в противофазе |
Рис. 4.5. Напряжения находятся в квадратуре |
Если
угол
![]() ,
то два напряжения совпадают по фазе
(рис. 4.3).
,
то два напряжения совпадают по фазе
(рис. 4.3).
Если
угол
![]() ,
то говорят, что напряжения находятся в
противофазе (рис.4.4).
,
то говорят, что напряжения находятся в
противофазе (рис.4.4).
Если
угол
![]() ,
то напряжения находятся в квадратуре
(рис. 4.5).
,
то напряжения находятся в квадратуре
(рис. 4.5).
В большинстве случаев оказывается неудобным пользоваться амплитудным, а тем более мгновенным значением тока или напряжения, поэтому наиболее часто используется действующее значение тока I, в основу определения которого положено тепловое действие тока.
Под действующим или среднеквадратичным значением переменного периодического тока I, (напряжения U или ЭДС E) понимают величину которая рассчитывается следующим образоом

Это соотношение характеризует среднее за период значение мощности, выделение теплоты в цепи с сопротивлением r
![]()
т.е. действующее значение переменного периодическго тока равно такому постоянному току, который, проходя через сопротивление r, за период Т выделяет то же количество тепла, что и данный переменный ток i.
Так при синусоидальном токе :
 .
.
Среднее значение синусоидальной величины за период равно нулю, поэтому говорят о среднем значении за положительный полупериод:

Среднее значение тока меньше действующего.
4.2. Законы Кирхгофа и Ома в комплексной форме
Для синусоидальных сигналов законы Кирхгофа и Ома удобно записывать в комплексной форме.
При комплексном представлении гармоническое колебание как функция времени заменяется комплексной амплитудой, т.е. комплексным числом, не зависящим от времени. Это делается для упрощения записи и выполнения операций над гармоническими функциями.
Вспомним комплексные числа. Z – комплексное число. Его можно записать в одной из трех форм: алгебраической, показательной и тригонометрической.
Z = a + jb
=
![]() ,
,
где a = Re [Z] = A cos ; b = Im[Z] = A sin.
R e –
реальная часть, Im
– мнимая часть комплексного числа. На
рис. 4.6 показано геометрическое
представление комплексного числа на
комплексной плоскости.
e –
реальная часть, Im
– мнимая часть комплексного числа. На
рис. 4.6 показано геометрическое
представление комплексного числа на
комплексной плоскости.
А – mod[Z] – модуль комплексного числа Z, или А = (а2+b2)1/2 – длины векторов комплексного числа.
φ = arg[Z] – аргумент комплексного числа Z, или φ = arctg(b/a) – начальная фаза.
Выражение Аmej(ωt+φ) называют комплексом гармонической функции. Тогда, учитывая, что Аcosφ = Re{Aejφ}, можно записать
![]()
 .
.
К
омплексную
величину
![]() называют комплексной амплитудой
гармонического сигнала, а еjωt
– множителем вращения. Комплексная
амплитуда содержит информацию о двух
важнейших параметрах гармонического
сигнала – об амплитуде и начальной
фазе. Комплексная амплитуда и гармоническая
функция времени при известной частоте
ω связаны взаимнооднозначно, т.е.
называют комплексной амплитудой
гармонического сигнала, а еjωt
– множителем вращения. Комплексная
амплитуда содержит информацию о двух
важнейших параметрах гармонического
сигнала – об амплитуде и начальной
фазе. Комплексная амплитуда и гармоническая
функция времени при известной частоте
ω связаны взаимнооднозначно, т.е.
![]() .
.
Пример 1.
Например, гармоническому колебанию
u(t)
= 256 cos(2π100t
– 45)
соответствует комплексная амплитуда
![]() m
= 256 e–j45.
m
= 256 e–j45.
Справедливо и обратное. Если известна комплексная амплитуда гармонического сигнала m = 256 e–j45 и частота ω=2π100, то этому соответствует гармоническое колебание u(t) = 256 cos(2π100t – 45).
Геометрически комплексная амплитуда представляет собой вектор, характеризуемый модулем и фазой, равными, соответственно, амплитуде и начальной фазе гармонической функции, как это показано на рис. 4.7,

Рис. 4.7. Комплексная амплитуда напряжения
![]()
оператор вращения,
представляющий собой единичный вектор,
умножение на который комплексной
амплитуды напряжения
оператор вращения,
представляющий собой единичный вектор,
умножение на который комплексной
амплитуды напряжения
![]() означает
вращение вектора комплексной амплитуды
против часовой стрелки с угловой частотой
означает
вращение вектора комплексной амплитуды
против часовой стрелки с угловой частотой
![]() .
.
Законы токов и напряжений Кирхгофа можно записать как для мгновенных значений токов и напряжений, так и для комплексных амплитуд этих токов и напряжений:
 ,
,

закон токов Кирхгофа в комплексной
форме для комплексных амплитуд и
действующих значений в комплексной
форме,
закон токов Кирхгофа в комплексной
форме для комплексных амплитуд и
действующих значений в комплексной
форме,
,
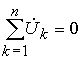
закон напряжений Кирхгофа в комплексной
форме.
закон напряжений Кирхгофа в комплексной
форме.
Пример 2. Рассмотрим пример использования законов Кирхгофа в комплексной форме. Пусть имеется узел в цепи, к которому подключены четыре ветви, как это показано на рис. 4.8.

Рис. 4.8. Узел цепи
В первых трех ветвях ток направлен к узлу, а в четвертой он направлен от узла. Все токи синусоидальные и параметры трех из них известны:
![]() ;
;
![]() ;
;
![]()
Требуется определить четвертый ток.
Для решения этой задачи необходимо все токи перевести в комплексную форму, т. е. нужно записать их комплексные амплитуды:
![]() ,
,
![]() ,
,
![]() .
.
Затем необходимо воспользоваться законом токов Кирхгофа в комплексной форме для комплексных амплитуд токов:
![]() .
.
И, наконец, по найденной комплексной амплитуде четвертого тока можно записать его временную функцию:
![]() .
.
Эту задачу можно решить графически с помощью векторной диаграммы, которая представляет собой картину расположения векторов токов и напряжений на комплексной плоскости. Для этого, как показано на рис. 4.9, на комплексной плоскости нужно отложить три вектора комплексных амплитуды известных токов, а вектор комплексной амплитуды можно построить путем суммирования векторов комплексных амплитуд известных токов на основе закона токов Кирхгофа.

Рис. 4.9. Векторная диаграмма
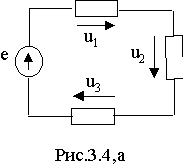
Пример 3. Известны мгновенные значения напряжений на элемен-тах контура ( рис.3.4,а) u1= 10 Sin( 100t-45o) B, u2= 25 Sin( 100t+30o)B, u3= 5 Sin( 100t+60o)B. Требуется определить мгновенное значение ЭДС источника напряжения.
|
|
Решение. На основании второго закона Кирхгофа для мгновен ных значений напряжений и ЭДС находим e= u1+ u2+ u3.
Переходя
к комплексам, получим
![]() ,
где
,
где
![]() .
.
Следовательно,
![]() =
=
10Cos45o-j10Sin45o+25Cos30o+j25Sin30o +5Cos60o + j5Sin60o =
=30.75+j9.75=![]() =
32.3ej18в.
=
32.3ej18в.
Построив вектора напряжений на комплексной плоскости (рис.3.4,б ) убеждаемся, что сумма их действительно равна вектору ЭДС. Переходя от комплекса к мгновенному значению, получим e= 32.3 Sin( 100t+18o), В.
Комплексное сопротивление и комплексная проводимость
Закон Ома в комплексной форме связывает комплексы напряжения и тока:
![]() ,
,
![]() ,
,
 .
.
![]()
комплексное
сопротивление двухполюсника. Комплексное
сопротивление представляет собой
комплексное число или вектор, который
можно отложить на комплексной плоскости
(рис.4.14).
комплексное
сопротивление двухполюсника. Комплексное
сопротивление представляет собой
комплексное число или вектор, который
можно отложить на комплексной плоскости
(рис.4.14).

Рис. 4.14. Комплексное сопротивление двухполюсника
![]() -
комплексная проводимость, величина,
обратная комплексному сопротивлению:
-
комплексная проводимость, величина,
обратная комплексному сопротивлению:

Комплексные сопротивления и проводимости элементов складываются по тем же правилам, что и сопротивления и проводимости R-элементов. Например, в цепи рис. 4.15 комплексные сопротивления элементов в последовательном контуре суммируются, а напряжение источника, согласно закону Ома в комплексной форме, связано с током в контуре следующим выражением:
![]() .
.

Рис. 4.15. Цепь с последовательным соединением элементов
Ток в контуре, соответственно, можно определить:
 ,
где
,
где
![]()
общее или входное сопротивление контура.
общее или входное сопротивление контура.
Пример 4. Через зажимы двухполюсника с комплексным сопротивлением Z=40ej30 Ом протекает синусоидальный ток =3 Sin (314 t + 15o) A. Определить напряжение u(t) на зажимах двухполюсника.
Решение.
Находя комплексную амплитуду тока
![]() =3е
j15
и зная комплексное сопротивление
двухполюсника, на основании закона Ома
в комплексной форме определяем
комплексную
амплитуду напряжения
=3е
j15
и зная комплексное сопротивление
двухполюсника, на основании закона Ома
в комплексной форме определяем
комплексную
амплитуду напряжения
![]() =3е
j15 40ej30=120
е j45
В.
=3е
j15 40ej30=120
е j45
В.
Следовательно, мгновенное напряжение равно u=120 Sin (314 t + 45o), B.