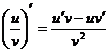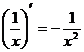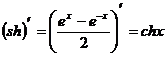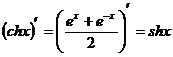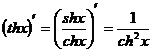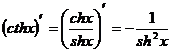Механический смысл производной

Пусть прямолинейное движение материальной точки задано законом S = S(t). Путь, который проследует точка за время ∆t равен ∆S = S(t+∆t)-S(t). Средняя скорость есть  , мгновенная скорость  .

Пример.

Пусть дан закон движения материальной точки  , найти скорость точки через t = 3 сек.

.

Дифференциал функции

Пусть задана функция y = f(x) на интервале (a,b). Функция y = f(x) дифференцируемой в точке x, если ∆y можно представить с помощью следующего выражения:

∆y = A∆x + α(∆x)∆x,

где А= const при фиксированном  х и   при  .

Теорема. Для дифференцируемости функции в точке х необходимо и достаточно, чтобы функция имела в этой точке конечную производную.

Дифференциалом функции y = f(x) называется выражение вида dy=A  - это главная линейная часть приращения ∆y , на основании предыдущей теоремы  , обозначив дифференциал независимой переменной через dx=∆x, получим  выражение для дифференциала функции:

.

Геометрический смысл дифференциала виден из следующего рисунка

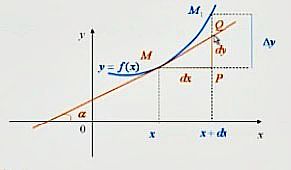
, т.е. дифференциал функции равен отрезку PQ это приращение ординаты касательной, а приращение функции ∆y это отрезок  .

Формулы дифференцирования

Таблица производных

Производная сложной функции

Если y = f(x) и u = u(x), то есть y=f[u(x)] сложная функция, где функции f(u) и u(x) имеют производные, то

это правило дифференцирования сложной функции.

Пример.

 

Производная обратной функции

Пусть задана функция y = f(x), тогда определена обратная функция x = ϕ(y). Для функции y = 5x обратная функция  , для функции   обратная функция  .  Пусть функция y = f(x) возрастает или

убывает на (a,b) и непрерывна, тогда существует обратная функция x = ϕ(y) и ее производная

.

Примеры. Найти производную обратной тригонометрической функции y = arcsinx.  Обратная функция  x = siny и  , по формуле для обратной функции  .

Найдем   функции  y = arctgx. Обратная функция  x = tgy,   .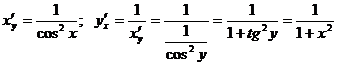

3.Теория интегралов

Основные методы интегрирования

Определение интеграла, определенный и неопределенный интеграл, таблица интегралов, формула Ньютона-Лейбница, интегрирование по частям.

Неопределенный интеграл

Функция F(x), дифференцируемая в данном промежутке X, называется первообразной для функции f(x), или интегралом от f(x), если для всякого x ∈X справедливо равенство:

F^' (x) = f(x).                                              (3.1)

Нахождение всех первообразных для данной функции называется ее интегрированием. Неопределенным интегралом функции f(x) на данном промежутке Х называется множество всех первообразных функций для функции f(x); обозначение -

∫ f(x) dx.

Если F(x) - какая-нибудь первобразная для функции f(x), то

∫ f(x)dx = F(x) + C,                                         (3.2)

где С - произвольная постоянная.

Таблица интегралов

Непосредственно из определения получаем основные свойства неопределенного интеграла и список табличных интегралов:

1) d ∫ f(x)=f(x)dx,

2) ∫df(x)=f(x)+C,

3) ∫af(x)dx=a ∫f(x)dx (a=const),

4) ∫(f(x)+g(x))dx= ∫f(x)dx+ ∫g(x)dx.

Список табличных интегралов

1. ∫x^ dx = x^+1/( + 1) +C; ( ≠ -1).

2. = ln x +C.

3. ∫ a^x dx = a^x/ln a + C (a>0, a ≠1).

4. ∫e^x dx = e^x + C.

5. ∫sin x dx = cos x + C.

6. ∫cos x dx = - sin x + C.

7.  = arctg x + C.

8.  = arcsin x + C.

9.  = tg x + C.

10.  = - ctg x + C.

 

Замена переменной

Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.

Если функция f(z) непрерывна на [, ], функция z =g (x) имеет на [a,b] непрерывную производную и α ≤ g(x) ≤ β, то

∫ f(g(x)) g^' (x) dx = ∫f(z) dz,                                   (3.3)

причем после интегрирования в правой части следует сделать подстановку z=g(x).

Для доказательства достаточно записать исходный интеграл в виде:

∫ f(g(x)) g (x) dx = ∫ f(g(x)) dg(x).

Например:

1)  ;

2) .