1.Теория пределов

ПРЕДЕЛ  ФУНКЦИЙ. Предел переменной величины. Бесконечно большая переменная величина

 В этом параграфе мы будем рассматривать упорядоченные пере­менные величины, изменяющиеся  специальным образом, который определяется терминами «переменная величина стремится к пределу». Во всем дальнейшем курсе понятие предела переменной будет играть фундаментальную роль, так как с ним непосредственно связаны основные понятия математического анализа -производная, интеграл и др.

 Определение 1. Постоянное число а называется пределом переменной величины х, если для каждого наперед заданного произвольно малого положительного  числа   можно указать такое значение пе­ременной х, что все последующие значения переменной будут удов­летворять неравенству

   

 Если число     есть предел переменной величины х, то говорят, что х стремится к пределу  , и пишут:

    или  . 

 В терминах геометрических определение предела может быть сформулировано следующим образом:

 Постоянное число     есть предел переменной, если для любой наперед заданной как угодно малой окрестности с центром в точке   и радиусом   найдется такое значение х, что все точки, соответ­ствующие последующим значениям переменной, будут находиться в этой окрестности.

  Замечание 1. Постоянную величину с часто рассматривают как величину переменную, все значения которой одинаковы:  х = с.

 Очевидно, что предел постоянной будет равен самой постоянной, т.к. всегда выполняется неравенство   при любом  .

 Замечание 2. Из определения предела следует, что переменная величина не может иметь двух пределов. Действительно, если   и  , , то х должен удовлетворять сразу двум неравенствам:

 

при произвольном малом  , а это невозможно, если 

 Замечание  3. Не следует думать, что каждая переменная величина имеет предел. Пусть переменная величина хпоследовательно принимает следующие значения   

 

 

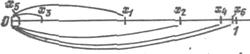
 При достаточно большом k значение  , и все последую­щие значения с четными номерами будут отличаться как угодно мало от единицы, а следующее значение   и все последующие значения х с нечетными номерами будут как угодно мало отли­чаться от нуля. Следовательно, переменная х не стремится к пределу.

 В определении предела указано, что если переменная величина стремится к пределу  , то    - постоянное число. Но понятие «стре­мится» употребляется и для характеристики другого способа изме­нений переменной величины, что видно из следующего определения.

 Определение  2. Переменная х стремится к бесконечности, если для каждого наперед заданного положительного числаМ можно указать такое значение х, начиная с которого все последующие значения переменного будут удовлетворять неравенству   .

 Если  переменная х стремится к бесконечности, то ее называют бесконечно большой переменной величиной и пишут  .

Предел функции

  Рассмотрим  некоторые случаи изменения функции при стремлении аргумента х к некоторому пределу а или к бесконечности.

 Определение 1. Пусть функция   определена в некоторой окрестности точки а или в некоторых точках этой окрестности. Функция   стремится к пределу   при х, стремящемся к  , если для каждого положительного числа  , как бы мало оно ни было, можно указать такое положительное число  , что для всех х, отличных от    и удовлетворяющих неравенству  , имеет место неравенство 

  .

Если   есть предел функции f(x) при  , то пишут:   или f (x)  при  .

 Если   при  , то на графике функции  , т.к. из неравенства   следует неравенство  , то это значит, что для всех точек х, отстоящих от точки   не далее чем на  , точки М  графика функции  лежат внутри полосы шириной  , ограниченной прямыми    и   .

 

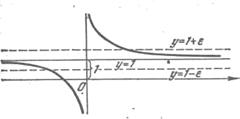   Рассмотрим переменную величину у = f (х). При этом считать, как и всюду в дальнейшем, что из двух значений  функции последующим является то значение, которое соответствует последующему значению аргумента. Если определенная так переменная величина у при   стремится к некоторому пределу  , то будем писать

 

и говорить, что функция у = f (х) стремится к пределу b при  .

 Легко доказать, что оба определения предела функции эквива­лентны. Замечание.

 Если f (x) стремится к пределу b₁ при х, стре­мящемся к некоторому числу   так, что x принимает только значения, меньшие  , то пишут   и называют b₁ пределом функ­ции f(x) в точке   слева. Если х при­нимает только значения большие, чем  , то пишут   и называют b₂, пределом функции в точке    справа.

 Можно доказать, что если, предел справа и предел слева существуют и равны, т. е.  , то b и будет пределом в смысле данного выше оп­ределения предела в точке  . И об­ратно, если предел функции b в точке  , то существуют пределы функции в точке    справа и слева и они равны.

 Замечание.

 Для существования предела функции при   не требуется, чтобы функция была определена в точке  . При нахождении предела рассматриваются значения функции в окрестности точки  , отличные от  ; это положение наглядно иллю­стрируется следующим примером.

 Пример.  Докажем, что  . Здесь функция   не определена при х = 2.

 Нужно  доказать, что при произвольном   найдется такое  , что будет выполняться неравенство 

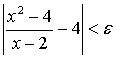  , (1.1)

если | х — 2 | <  . Но при х 2 неравенство (1) эквивалентно неравенству

   (1.2)

или  . 

Таким  образом, при произвольном   неравенство (1.1) будет выполняться, если будет выполняться неравенство (1.2) (здесь   ). А это и значит, что данная функция при   имеет пределом число 4.

Рассмотрим  некоторые случаи изменения функции при  . Определение 2. Функция f(x) стремится к пределу  , если для каждого произвольно малого положительного числа   можно указать такое положитель­ное число N, что для всех значении х, удовлетворяющих н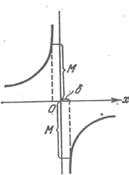 еравенст­ву  , будет выполняться неравенство  .

  Зная смысл символов:   очевидным является и смысл выражений:

    стремится к b при   и

    стремится к b при  ,

 которые символически записываются так:

  ,  .

Основные правила нахождения пределов

Предел постоянной величины равен постоянной величине:

Предел суммы равен сумме пределов:

Предел разности равен разности пределов:

Предел произведения равен произведению пределов:

Предел отношения равен отношению пределов:

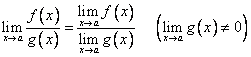
Предел функции в степени:

Предел корня из функции:

Основные пределы

Первый замечательный предел:

Второй замечательный предел:

Другие полезные формулы пределов:

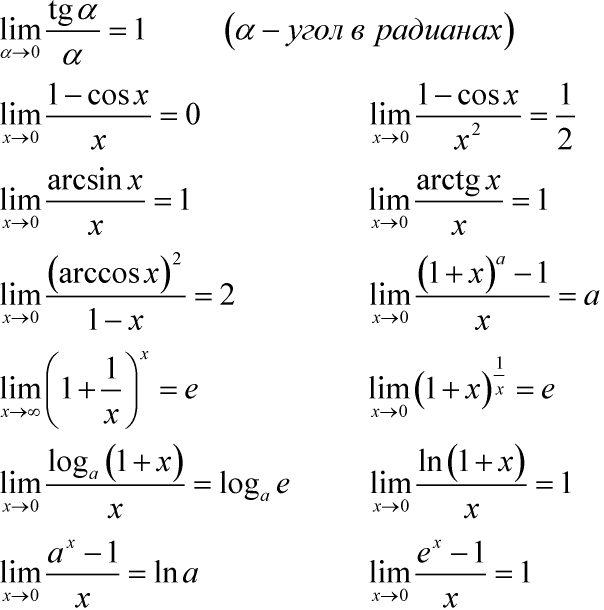
Бесконечно малые

Эквивалентность бесконечно малых:

Правила Лопиталя.

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить неопределенности   или   .

Первое правило Лопиталя 

Рассмотрим функции  , которые бесконечно малы в некоторой точке  . Если существует предел их отношений  , то в целях устранения неопределённости   можно взять две производные – от числителя и от знаменателя. При этом:  , то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел   тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного  !!!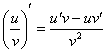

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость  .

К данной неопределённости применим первое правило Лопиталя: Не редкость, когда правила Лопиталя приходится применять последовательно два или большее количество раз (это относится и ко второму правилу).

Применим правило Лопиталя:

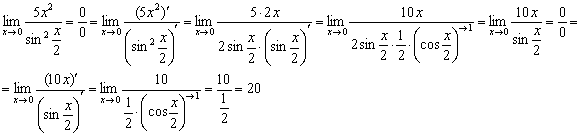
Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).