Экзамен / Экзамен по физике. ОГТУ. (3 семестр) / Физика / shmel - fix4

Фононы. Можно представить как поток корпускул каждый фотон. Можно аналогично отквантовать и упругую волну, т.е. она у нас будет как поток квазичастиц фононов. Фонону дают энергию _ф=ħω (где ħ- постоянная Планка, которая без 2,т.е. ħ =h/2; ω-частота) и квазиимпульс k_ф=2/ (где –длина волны упругих смещений) Энергия упругой волны будет суммой _ф: _i(_ф)=_i(ħω) Энергия гармонического осциллятора: ε_n=(n+)*ħω.(где n-целое число) Фононы не подчиняются статистике Ферми и не являются фермионами, фононы – бозоны, они подчиняются статистике Бозе-Эйнтштейна, т.е. в одном и том же состоянии может быть сколько угодно фононов. Причём: n_i=1/[exp(ħω_i/kT)-1] (где n_i- среднее число фононов с частотой ω_i; Т-температура; k-постоянная Больцмана). Если температура велика kT >> ħω_i; т.е. exp(ħω_i/kT)≈1+ħω_i/kT. Значит : n_i=(kT)/(ħω_i). Т.о. среднее число растет с температурой. Фононы при сталкновениях обмениваются квазиимпульсом и т.е. тепловое сопротивление, это сопротивление растёт с температурой.

Свободные электроны в металле. Если выделить е в металле и построить зависимость потенциальной энергии от координаты: ( здесь + -ионы кристаллической решетки). Это приводит к тому, что энергетические уровни можно представить в виде зон. Можно заменить некоторым средним

значением. Т.к. металл трёхмерный, то яма трёхмерная (это учтём потом). Решим уравнение Шредингера когда электрон в такой яме. Δφ+2m/ħ²*E_φ=0(1).(где Δ – лапласиан,он трёхмерный; Е-энергия е, φ-волновая функция, m-масса е, ħ- постоянная Планка) Мы для удобства принимаем, что в середине ямы U=0. сместим начало отсчёта. φ=А*ехр[i(kr-ωt)] (2) (где i=; ω- циклическая частота, r- радиус-вектор e, k- волновой вектор(k=2π/λ), t-время, A- коэффициент). Волновые функции будут плоскими монохроматическими волнами, т.к. (2) – уравнение плоской монохромной волны. Полная энергия т.к.U=0, равна кинетической: E=E_k=p²/2m=ħ²k²/2m, (где р- импульс) .sinkL=0 на границе ящика  kL=nπ  k=nπ/L(*) (где n – целое число, L – линейный размер Ме; k-волновое число). Т.к. яма трёхмерная получаем сумму проекций k на оси координат: k²=k_x²+ k_y²+k_z². Используя (*): k²=(π/L)²(n_x²+n_y²+n_z²) (где n_x, n_y, n_z – квантовые числа), тогда: E=ħ²k²/2m  E=(1/2m)*(πħ/L)²(n_x²+n_y²+n_z²). Энергетический спектр зависит от 3-х квантовых чисел. Пусть: 1)L 10^-10м, то Е~1эВ. 2) L~1см, то E_nx+1-E_nx~10^-16эВ при n_y,n_z=const. Энергетические уровни располагаются очень рядом. (здесь E_f- полная энергия на уровне Ферми; W_kf-кинетическая энергия на уровне Ферми). Причём каждый энергоуровень занят двумя е, т.к. они фермионы. Эти 2 е занимают нижние энергетические состояния. Можно отделить уровни занятые электронами и не занятые. Уровень Ферми – энергоуровень, отделяющий занятые от незанятых. Максимальная энергия е равна W_kf Полная энергия Ферми, т.е. энергия е на уровне Ферми: E_f=E_пот.+Е_кин.=U₀+W_kf. Найдём W_kf: W_kf=р_f²/2m (где р-импульс е (максмальный) на уровне Ферми; m-масса е) Найдём р_f: р_f²=р_{x max}²+р_{y max}²+р_{z max}², (где р_{x max} , р_{y max} , р_{z max} - проекции на координатные оси). Импульс равен р=kħ  р²=ħ²k²=(πħ/L)²(n_x²+n_y²+n_z²) = (ħ²/4L²) (n_x²+n_y²+n_z²). Используя выражение для импульса(то что выведено через k и видно в выражении для энергии см выше). Вспомним ħ=h/2π, получаем: р_{x max}²=h²n_{x max}²/4L²; р_{y max}²=h²n_{y max}²/4L²; р_{z max}²=h²n_{z max}²/4L² (**)(где n_{x max}² , n_{y max}² , n_{z max}² – максимальные квантовые числа). Пусть у нас металл – куб с ребром L и T=0°К. Каждая компонента импульса не может быть больше р_f. р_{x max}=р_{y max}=р_{z max}=р_f. Из выражений (**) найдём n_{x max} , n_{y max} , n_{z max}: n_{x max}=n_{y max}=n_{z max}=2L*р_f /h. Число состояний заполненных электронами т.к. на каждом по 2 штуки равно: N=N_э (где N_э – число е). Рассмотрим всё пространство чисел n_x n_y n_z и каждому набору этих чисел поставим точку. Совокупность точек даёт решётку с постоянной равной 1. Эта решётка отрубит  сферы (в этом куске будут все те точки) с радиусом R=2L*р_f /n.Объём этого куска сферы: V=*πR³=4/3π(2L*р_f /h)³. Такой объём равен сумму объёмов элементарных ячеек заполняющих объём. Ребро элементарной ячейки равен постоянной решётки = 1. Объём значит такой элементарной ячейки равен 1³=1. Получается что объём общий сегмента совпадёт с числом элементарных ячеек. И на 1 элементарную ячейку приходится по 1-й точке. Объём значит совпадёт с числом заполненных состояний, т.е. V=N=N_э=*π(2L*р_f /h)³; N_э=π/3(2L*р_f /h)³; N_э=(8π*L³р_f³)/(3h³) р_f=³[(3h³N_э)/(8πL³)]=h*³(3n/π), (где n- плотность электронов, n=N_э/L³=N_э/V), Значит: W_kf=р_f²/2m=[h²*³(9n²/π²)]/2m; Итак максимальное значение кинетической энергии е в металле при T=0°К: W_kf=(h²/m)*³(9n²/π²).; Число атомов в единице объёма n_a=n=10²²-10²³см^-2  W_kf≈(4-9)эВ.. Из-за тепловых пунктуаций e переходят выше уровня Ферми. Тепловое движение в металле приводит к увеличению на чуть-чуть энергии e. 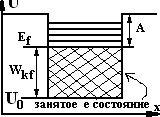Расстояние между уровнем Ферми и уровнем, когда е выходят в вакуум обзовем A – работа выхода: U₀=|A+W_kf|; полная энергия это сумма: E_f=(E_{потенц.}+Е_кин.)_f= -U₀+W_kf Значит E_f = -(A+W_kf)+W_kf= -A-W_kf+W_kf= -A

Контактная разность потенциалов. Контактная разность потенциалов – это разность потенциалов приведённых в контакт. Если соединить 2 разных металла возникают заряды на межфазной границе. Пусть есть два металла. и мы их соединяем: Работа выхода у I <II.  Электроны из металла I будут идти во II и занимать состояния энгергетичеки ниже уровня Ферми. Значит металл I будет заряжаться «+», а Ме II - отрицательно. Потенциальная энергия в металле I уменьшается, а в II – растёт. В итоге уровни Ферми уровняются, т.к.придет время, когда j₁₂=j₂₁, (где j – поток е). Получится . Диаграммы сдвинутся на ΔU. Δφ=ΔU/e; ΔU=(A₂-A₁)/e; (где A₂, A₁ – работа выхода, Δφ – контактная разность потенциалов). В конденсированных средах частицы связаны силой и значит для описания состояний надо задать функцию распределения.

Распределение частиц по энергиям. Рассмотрим ансамбль взаимодействующих частиц одного вида. n – общее число частиц ансамбля. Для частиц dn, у которых энергии в пределах от E до E+dE, то число частиц в этом интервале пропорционально интервальной длине, т.е. dn=N(E)dE, (где N – коэффициент, зависящий от энергии. N(E) – функция распределения частиц по энергиям) . N(E)=D(E)* f(E), (где D(E) – коэффициент пропорциональности, или D(E) – плотность состояний с энергией Е; f(E) – вероятность того, что отдельная частица ансамбля имеет энергию Е). Зависимо от законов, описывающих взаимодействие частиц: распределение квантовое и распределение классическое. При равновесном состоянии – равновесная функция распределения; при неравновесном – неравновесная функция. 1)Распределение Максвелла-Больцмана. Пусть есть газ из одного вида молекул. dn=N_МБ(E)dE, (где N_МБ– функция распределения Максвелла-Больцмана). N_МБ(E)=D_МБ(E)f_Б(E);(где f_Б(E) – вероятность того, что энергия у классической частицы будет Е; D_МБ(E) – коэффициент). f_Б(E)=ехр(-Е/КТ). D_МБ(Е)=n[2E/(KT)³]; Само распределение Максвелла-Больцмана имеет вид:. Пусть у нас теперь квантовые взаимодействия. 2)Распределение Ферми-Дирака. Пусть система в равновесии, но наш ансамбль из n частиц состоит из фермионов(допустим эти фермионы – e в металле). dn=N_ФД(Е)dE; N_ФД=D_ФД(Е)f_ФД(Е). Частицы фермионы подчиняются принципу Пауля и найдем f_ФД(Е). Пусть у нас Ме с температурой 0°K. Если E < E_f, то вероятность обнаружить е будет равна 1.(где E – энергия е, E_f – энергия Ферми) Если E > E_f, то вероятность обнаружить е будет равна 0, т.е. наша зависимость f_ФД(E) представляется как ступень. Пусть теперь метал имеет T≠0°K. Рассмотрим энергетические состояния E-E_f>>КT; (где К – постоянная Больцмана). Число e с такими энергиями мало по сравнению с разрешёнными энергосостояниями. Т.о. принцип Пауля не влияет на распределение е по энергиям.f_ФД(E)=exp[-(E-E_f)/KT] Соединяем эти два случая, получим выражение для f_ФД(E) общего вида. Распределение Ферми-Дирака: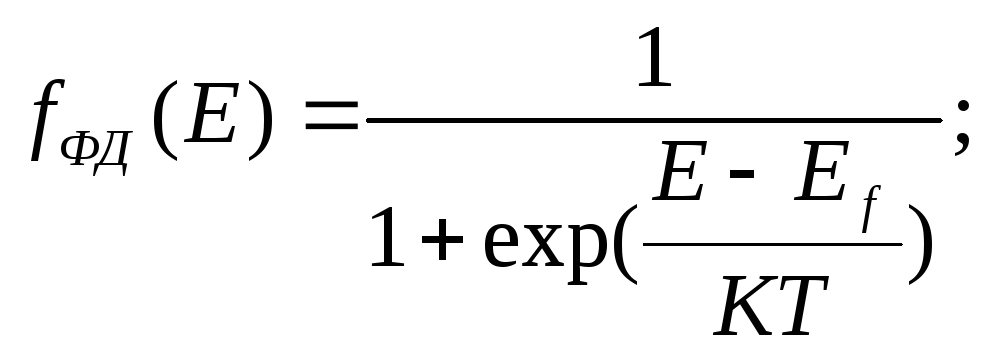 Это действительно при T→0, (E< E_f), то exp(-∞)=0, т.е. f_ФД(E) → 1, а при E > E_f, и Т→0, то f →0, ну а тогда T≠0, и E- E_f >> kT, у exp большой показатель, получаем, что f≈exp(-(E- E_f)/KT); При E=E_f; f_ФД(E_f)=1/2; (пунктирная линия симметрична относительно E_f) ;(где D_ФД – плотность состояний; V – объём Ме, E – энергия е; h – постоянная Планка, m^*- эффективная масса е.). Эффективная масса отлична от массы е, ведь в металле на е действуют разные поля, а в вакууме нет. N_ФД(Е)=D_ФД(Е)-f_ФД(Е). Когда энергия мала, т.е. < E_f, то определяет всё D_ФД(Е), а далее рулит f_ФД(Е). Т.о. в случаях когда число частиц соизмеримо с числом возможных энергосостояний надо использовать квантовое распределение Ферми-Дирака, если же число разрешённых энергосостояний немного больше числа частиц занимающих эти состояния можно использовать классическое (Максвелла-Больцмана).

Распределение Бозе-Эйнтштейна. Пусть есть ансамбль из n частиц и частицы в нем бозоны(с целыми квантовыми магнитными числами). Тогда: f_БЭ(E)=1/[exp((E-E_f)/KT)-1] Здесь отличие в том, что при понижении температуры ниже критического значения появляется второго рода фазовый переход(T<T_кр) при T_кр бозоны оказываются в одном состоянии с нулевым импульсом. T_кр – температура вырождения(критическая температура). Эффект сверхтекучести гелия: фононовый газ переходят в состояние с импульсом в 0. Жидкость не может обмениваться импульсом как со стенками так и с другими фононами . Сверхпроводимость тоже объясняется этим. Её рассматривают как сверхтекучее состояние в проводниках. Электроны объединяясь в куперовские пары дают спин равный 0(т.е. +1/2; U^-1/2). Каждый электрон поляризует кристаллическую решётку и между двумя электронами появляются силы притяжения и электроны объединяются в куперовские пары. Получаем уже газ бозонов, что по распределению Бозе-Эйнтштейна и даёт сверхпроводимость.

Зонная теория твёрдых тел. Мы вели среднее значение . При усреднении мы получали. Если учитывать периодичность, то зоны будут разрешённые и неразрешённые. Вот и получится зонная структура. Пусть есть 2 одинаковые потенциальные ямы. Если поместить е в одну, а потом в другую, мы получим одинаковые энергетические уровни: . Поставим ямы рядом:. Теперь поместив электрон в одну яму мы получим иной результат(т.е. изменилось решение квантовой задачи). Тогда энергетический спектр электрона будет смещённым. Если их объединить, то будет по паре. Т.е. раздвоился. Возьмём теперь несколько ям рядом : и сделать с электроном аналогичное, то каждая яма даёт по одному уровню в каждую энергозону. Чем больше N, тем чаще распространяются зоны. У твёрдых тел каждый атом это яма, т.е. твёрдое тело будет такой кучей ям. . Энергетический спектр Na: (здесь ВЗ – валентная зона, ЗП – зона проводимости. R₀ – постоянная, при которой кристалл находится в устойчивом состоянии (минимум пот. энергии). R₀ – постоянная энергии кристаллической решётки). Валентные электроны могут легко переходить по энергоуровням в ЗП. Т.к. энергоуровни расположены по квазиуровням  е могут менять свою энергию квазинепрерывно. Т.к. зоны перекрывания и е могут увеличивать свою энергию и даёт натрию высокую электропроводимость и теплопроводимость. Энергетический спектр полупроводника или диэлектрика.

Основы физики полупроводников. Электроны и дырки в полупроводнике. Удобно рассматривать свойства при помощи зон. Случаи . 1 – при поглощении света, валентный е отрывается от атома, свободно перемещается по кристаллу, образуется «+»ион. Получается дырка, причём дырка может перемещаться по атомам, вероятность перемещения дырки высоко. Для (1) h≥ΔE – поглощение; 2- дырка и свободно перемещающийся е могут столкнуться и исчезает пара дырочно-электронная. Для (2) hυ’≈ΔE – излучение. Т.е. определив то излучение ’, получим ширину запрещённой зоны. Если полупроводник бомбардировать, то валентные е получат энергию от сталкивений с частицами полупроводника. В зависимости от природы полупроводника будут разные ширины запрещённых зон. Не всегда излучение бывает с выделением, т.е. идёт смесь рекомбинации излучательных и безизлучательных. Также электрон может перейти в зону проводимости из-за тепловых пунктуаций (из-за тепловой энергии кристаллической решетки). Вероятность того, что частица из кучки валентных электронов будет иметь энергию ε равна: p=exp(-ε/KT) { по закону Больцмана}. Необходимая энергия для перехода в зону проводимости: exp(-ΔE/KT). Сколько переходов идёт из ВП в ЗП столько и рекомбинирует в условиях равновесия (S=r) S – число прямых переходов в единицу времени, r – число обратных переходов в единицу времени. S = α*exp(-ΔE/KT); (где α – коэффициент, зависящий от природы материала и размера кристалла). r=βN^-*N⁺=β(N^-)², т.е. число е совпадает с числом дырок,(где β – коэффициент пропорциональности, N^-,N⁺– число е и дырок). Теперь приравняем S=r: α*exp(-ΔE/KT)=β(N^-)²  N^- =[(/)]*exp(-ΔE/2KT). Электропроводимость проводника  равна:

=₀exp(-ΔE/KT);(где ΔE – ширина запрещеной зоны, T – температура, ₀ – константа, зависящая от природы проводника). Собственные полупроводники – это полупроводники, у которых электропроводимость подчиняется =₀exp(-ΔE/KT). Если у них температура меняется, значит меняется и электропроводимость. ln=ln₀-(ΔE/2KT). Построим по данным зависимость: по направлению этой прямой и находят ΔE. Легированные полупроводники– полупроводники, содержащие примеси (инородные атомы). Легированные полупроводники - процесс введения в полупроводники примесей. Сначала плавят, потом добавляют примеси, потом всё это кристаллизуется. Легируем Ge. Ge: [Ar] 3d¹⁰4S²4p². Добавим в него мышьяка As: [Ar] 3d¹⁰4S²4p³. Атомы мышьяка заменяют в узлах решётки атомы германия т.е. у As по 4 соседа тоже. И у As химические связи такие же как и у Ge.У As есть ещё и 5 валентных электронов, но тут он уже не нужен. Этот лишний электрон слабо привязан к атому As. Оценим энергию этого кинутого электрона. Энергия для водорода: (где m – масса е, ħ – постоянная Планка e – заряд е),. Энергия связи E_св=E_∞-E₁=-E₁; при n=∞; E=0. Если мы берём для атома As в кристалле, то движение идёт не в вакууме, значит m меняем на m^* (эффективную массу). учитывая k₀=z/(4πεε₀). Из опыта: m^*/m ~ 0,1. Для Ge: ε_Ge=16  E_св ~ 0,01эВ. Из опыта вычислим: E_св=0,01эВ. Отсюда при небольшой температуре электрон может оторваться и перейти в зону проводимости (переход *). При Т=300ºК, N^-_AS Электропроводимость полупроводника определяется свободными электронами. Если

N^-_AS >> N^-_T число электронов возрастающих в зоне проводимости при легировании >> числа электронов от тепловых пунктуаций то это полупроводники n – типа. Примеси, которые дают электропроводимость – доноры. Донорский уровень образованный в запрещённой зоне локальный уровень. Легируем As Ga, получим: Ga:[Ar] 3d¹⁰4S²4p. Галлий тоже занимает узел в решетке по соседству с четырьмя. Но у него нет ещё одного электрона, для полноты, т.е. он не даёт одного электрона на одну гибридную связь. Из-за этого:. Атом галлия может легко отнимать электрон у соседа. As легко отдаёт, т.е. он положительно заряжен, а в случае Ga он легко захватывает, т.е. он отрицательно заряжен. Переход когда Ga захватил электрон на энергоуровень уровень - актепторный. Такой зазор небольшой и уже при Т=300ºК N⁺_Ga  N_Ga (число введённых атомов – примесей). Если число дырок появившихся от легирования намного больше числа дырок от тепловых пунктуаций, то это полупроводник “p” типа (N⁺_Ga >> N_T). Примесная электропроводимость – это электропроводимость полупроводников, обусловленная наличием примесей.

Движение электронов и дырок в кристаллах. Для частицы в вакууме волновая функция (где r- радиус – вектор частицы, k – волновой вектор, ω – циклическая частота. t – время. ћ – постоянная Планка; i=). =Е/ћ; Е=p²/2m=h²k²/2m Рассмотрим движение е в кристалле тут он движется в периодическом поле атомов  его скорость меняется периодически; средняя скорость постоянна. Найдём ускорение (а) под влиянием постоянной силы (F). Движение идёт в поле ионов кристаллической решетки. Будем рассматривать е как волновой пакет, т.е. будем считать волновую функцию е локализированной в некоторой области пространства. Групповая скорость (υ_гр) – скорость движения волнового пакета. υ_гр= dω/dk, т.к. ω=E/ ћ (где Е – энергия), то υ_гр=(1\ћ)*dE/dk;(где k – волновое число, k = 2π/λ, λ – длинна волны Де Бройля). Направим x по движению е . υ_x=(1/ћ)*dE/dk (1). По определению ускорение тогда a_x=dυ_x/dt=(1/ћ)*[(d/dk)*(dE/dt)]. Когда F = const, то dE=Fdx=δA. (фактически работа силы F по перемещению электрона на расстояние dx). Тогда dE/dt=Fdx/dt(производная от пути и значит это скорость)=Fυ_x; a_x=(1/ћ)*[(d/dk)*(dE/dt)]= =(1/ћ)*[(d/dk)*(F*υ_x)]=(F/ћ)*(dυ_x/dk)  т.к. F=const её вынесем. a_x=(F/ћ)*(1/ћ)*(d²E/dk²); запишим так: a_x=F/m^*, где m^* обозначает m^*=ћ²/(d²E/dk²). В кристалле е под действием F=const движется как классическая частица у которой масса определяется по m^*.(эффективная масса е). Можно найти E(k). Для разных кристаллов эта частица разная. Для дырки тоже можно так прорассуждать получить тоже самое, но d²E/dk² – производная от энергии дырки в зависимости от волнового числа, а m^* будет эффективной массой дырки.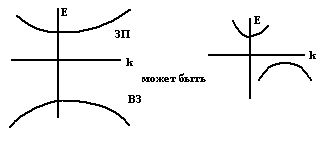

Если взять свободную частицу у которой энергия E=p²/dk²=ћ²/m, тогда эффективная масса m^*=ћ²/(ћ²/m)=m, т.е. равна массе