Раздел 2. Числовые и буквенные выражения.

Тема 2.1. Корни и степени

Самостоятельная работа№5-6 (4 часа)

Цель: повторить действия со степенями и корнями; повторить свойства степеней и корней.

Теоретические сведения.

1. При умножении степеней с одинаковыми основаниями показатели степеней складываются

2.При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого: = ^m-n

3. При возведении степени в степень показатели степеней перемножаются: = a^mn  

4. ^m =

5. ^{m =} .

6. a⁰ = 1

7. a^-n =

  Решите самостоятельно.

1. Упростите выражение: (-a)¹⁰ a³ (-a)⁶ ; a (-a)^-4aⁿ; -a⁴ a² (-a)⁶; -a ²a⁶ (-a)^2x

2. Найдите х, если: 6² ·x = 6³; x ·4²³ = 4²⁷; x· 2⁶ ·2⁹ = 2¹⁷; 3¹¹ ·3⁵ ·x = 3¹⁸

3. Найдите с: с ·a⁸ = a¹¹; a¹³· с = a¹⁶; c(a⁵ ·a⁸) = a¹⁷; (a ·a¹⁴ ) c= a²⁰

4. Вычислите: ; ; ;

5. Выполнить действия:

6. 7. 8.

9. 10. 11.

12. 13. 14.

15. 16. a- 17. 15a

18. 19. 10 20.

21. · 22. · 23. 24. 25. ( )· 26. ( )· 27. -

28. - 29. 30. 0,1· : - 2 31.

32. -6· + 33. : · 34. - 2 b 35. ·

36. ( )( - )

Упростить выражения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

Вопросы для самоконтроля. 

1.Формулы сокращённого умножения.

2.Правила действий со степенями.

3.Формулы корней сокращённого умножения.

4.Свойства числовых неравенств.

5.Понятие модуля.

6.Свойства пропорции.

Самостоятельная работа№7-8

Тема 2.2. Логарифмы. (2 часа)

Цель: Выработать навык логарифмических преобразований

Логарифм числа b по основанию a ( ) это показатель степени, в которую надо возвести число a, чтобы получить число b. (Логарифм существует только у положительных чисел).

Обозначение: (a > 0, a ≠ 1, b > 0)

= x, a^x = b.

Пример: = 3 , потому что 2³ = 8 .

Если, напр., основание будет 4, то =2; = 3; =1; =0,5; = -0,5; = 0; = -1

Десятичный логарифм - lg b (логарифм по основанию 10, а = 10)

Если возьмем за основание 10, то lg10=1; lg100=2; lg1000 =3; lg0,1 =-1; lg0,01 = -2; lg1 = 0;

Натуральный логарифм - ln b ( а = e).

Свойства логарифмов

1.    Основное логарифмическое тождество - a^loga^b = b;

2 .   log _a1 = 0;

3.    log _aa = 1;

4.    log _a (bc) = log _ab + log _ac;

5.    log _a(b/c) = log _ab – log _ac;

6.    log_a (1/c) = log _a1 – log _ac = - log _ac;

7.    log _a(b^c) = c log _ab;

8.    = (1/c) log _ab;

9.    Формула перехода к новому основанию log _ab =

10.    log _ab =

Переход от выражения к логарифму называется логарифмированием этого выражения.

Переход от логарифма к подлогарифмическому выражению называется потенцированием. Свойства логарифмов незаменимы при решении логарифмических уравнений и функций, упрощении примеров, также они пригодятся при решении интегралов и нахождении производной от логарифмов.

Примеры.

1. Вычислить:

(3log _a72 – log _a724) : (log _a73 – log _a79).

Решение: Используя свойства логарифмов, получим

(3log _a72 – log _a724):(log _a73 + log _a79)=(log _a72³ – log _a724):log _a727 = log _a73^–1: log _a73³ = – log _a73 : 3log _a73 = - ;

Ответ: - ;

2.Вычислить:

Решение: используя свойства степени, получим

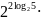
= = = = 5² ·3^-2 =2 5· =

Ответ:

 Вопросы для самоконтроля:

Что такое логарифм?

Какие свойства логарифма Вы знаете?

Как называется логарифм с основанием 10?

Как называется логарифм с основанием е?

Форма контроля: проверка конспекта.