5. Авторефераты диссертаций

1. Букаев П.Т. Разработка параметров оптимального процесса бесчелночного ткачества и критериев его оценки. Авторе ферат дисс. ... докт.техн.наук. - М.: ЛИТЛП, 1985. - 45 с.

2. Митрофанов О.Н. Разработка и исследование параметров наладки основного регулятора станка АТПР для стабилизации на тяжения нитей. Автореферат дисс. ... канд.техн.наук. - Ивано во: ИвТИ, 1985. - 15 с.

3. Примаченко Б.М. Разработка путей оптимизации процесса прибоя уточной нити на ткацких станках. Автореферат дисс. ... канд.техн.наук. - Л.: ЛИТЛП, 1985. - 18 с.

4. Степанов Г.В. Создание и технология получения техни ческих тканей для производства композиционных материалов. Ав ОПРЕДЕЛЕНИЕ НАТЯЖЕНИЯ ОСНОВНЫХ И УТОЧНЫХ НИТЕЙ В ПРОЦЕССЕ ФОРМИРОВАНИЯ ТКАНИ ЗАДАННОГО СТРОЕНИЯ.

3.1 Взаимосвязь между параметрами строения тканей и технологическими параметрами в процессе фронтального прибоя утка к опушке ткани.

При решении задач, связанных с изгибом текстильных нитей, следует особое внимание обратить на метод определения модуля упругости и момента инерции сечения нити. Обычно модуль упругости при изгибе существенно отличается от модуля упругости, получаемого при растяжении. Это объясняется тем, что строение волокон и нитей не однородно и изменяется во времени. Ясность в этот вопрос внес проф. Щербаков В.П. Он на большом экспериментальном материале показал, что отклонение значения модуля упругости при изгибе от модуля упругости при растяжении объясняется тем, что при изучении свойств нитей часто используется упругая модель, а не вязкоупругая, которая имеет место в действительности. Именно этим объясняется значительное расхождение между величинами модуля упругости при изгибе и модуля упругости при растяжении. Напряженное состояние волокна при изгибе является состоянием простого растяжения. Если каждое волокно можно считать находящимся в условиях простого растяжения, то модули упругости при растяжении и изгибе должны совпадать. Так как в опытах измерение происходит по истечении определенного времени, то фиксируется развившаяся во времени деформация. Рассчитанный на основе формул теории упругости, сопротивления материалов, модуль упругости при изгибе оказывается намного меньше, чем истинный модуль упругости, соответствующий мгновенному нагружению. При определении момента инерции сечения нити - сечение текстильной нити или пряжи не является сплошным.

y

N

M_и М_и

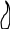
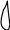
_{основа уток}

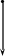
F_o у₁ y₁ h_o F_o

X

N/2 x₁ N/2

l_o=100/P_y

а)

y

N/2 N/2

М_и F_y F_y М_и

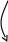
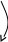
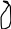
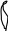
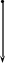y₂ h_y

_уток

x₂ X

N

l_у=100/P_о

б)

Рис.3.1 Геометрические модели строения тканей вдоль нитей основы (а) и утка (б).

Геометрические модели строения тканей полотняного переплетения представлены на рис.3.1. Для установления взаимосвязи между параметрами строения ткани и технологическими параметрами используются основные дифференциальные уравнения изгиба нитей основы и утка, которые имеют вид:

E_о J_о y₁" = M _и - x₁ + F_оy₁;

E_уJ_уy₂"= M_и - x₂+F_уy₂, (3.1)

где M_и – изгибающий момент;

N – сила нормального давления нитей основы и утка друг на друга;

F_o, F_y- натяжение основы и утка;

Е – модуль упругости нити;

J – момент инерции сечения нити.

Момент инерции сечения сплошной нити круглого сечения определяется по формуле:

J_o = 0,05d_o⁴ ; J_y =0,05d_y⁴ ; (3.2)

для эллипсообразного сечения – по формуле:

J_o = 0,05d_ord_oв³; J_y = 0,05d_yrd_yв³, (3.3)

где d_ог, d_уг – диаметр нити основы и утка в горизонтальном направлении,

d_ов, d_ув – диаметр нити основы и утка в вертикальном направлении.

Решение дифференциального уравнения нитей основы и утка имеет вид:

у₁ = c₁e ^kx1 + c₂e^-kx2-

y₂ = c₁e ^kx2 + c₂e^-kx2- (3.4)

где с₁,с₂ – константы интегрирования.

Не приводя здесь решения уравнений полностью (они даны в работах кафедры ткачества МГТУ имени А.Н.Косыгина) запишем окончательные уравнения:

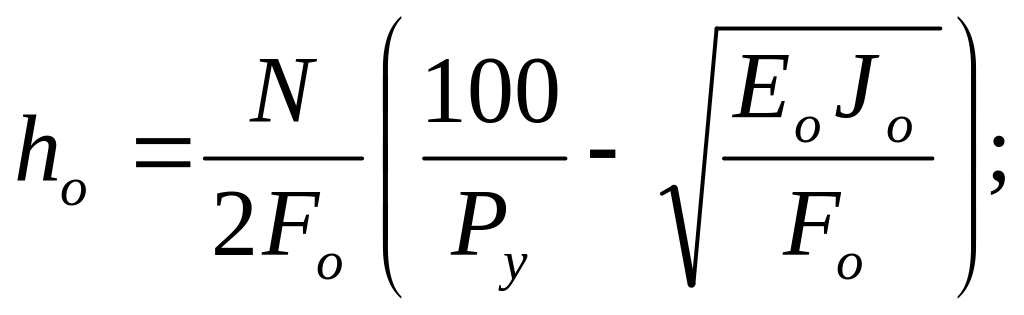
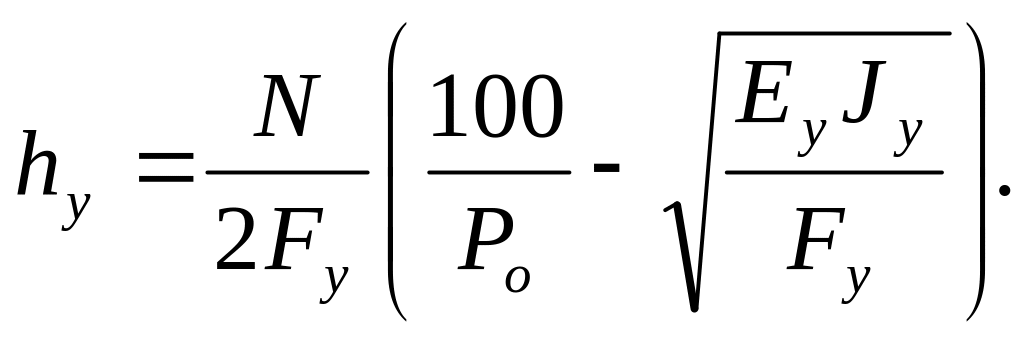(3.5)

Расчет следует проводить с учетом основного геометрического свойства однослойных тканей:

Кроме того , где - отношение высот волн изгиба основы и утка.

Порядок фазы строения .