№1. Основные понятия о графах

Граф G состоит из множества вершин Х и множества ребер U. Обозначение графа G=(X;U). Запись означает, что ребро графа образовано парой вершин и , , . Таким образом, ребра - это упорядоченные пары вершин.

С помощью графов можно отразить наиболее общие свойства объектов (топологические свойства), отвлекаясь от их геометрических форм и размеров.

Если для графа безразлично направление движения от вершины к вершине, то есть для каждого ребра несущественен порядок его концевых вершин, то граф называется неориентированным, для него .

Если для каждого ребра существенно направление, то граф называется ориентированным и - это различные ребра.

Пример:

В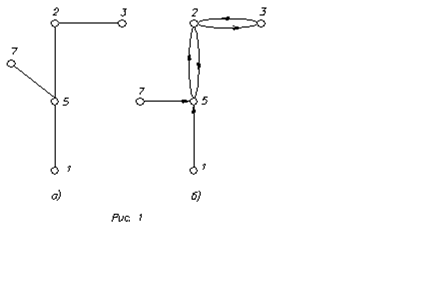 ершины: здания; ребра: прямые улицы

Мы будем изучать неориентированные графы. Две вершины и называются смежными, если существует ребро , соединяющее эти вершины. Говорят что ребро инцидентно вершинам , , если оно связывает эти вершины. Ребра , называются смежными, если они имеют общую вершину (в примере вершина l).

Если в графе любые две вершины связаны более чем одним ребром, то такой граф называется мультиграфом, а ребра связывающие одну и ту же пару вершин называются кратными. Наибольшее число кратных ребер в графе есть мультичисло.

Е сли в графе есть ребра у которых обе концевые вершины совпадают, то есть i=j, то такие ребра называются петлями (рис.2.).

Число ребер, инцидентных некоторой вершине называют степенью вершины, обозначается . Для графа риc.1,а . Легко увидеть, что если сложить степени всех вершин графа, то получится четное число равное удвоенному числу ребер, так как каждое ребро участвует в сумме 2 раза. Этот результат называют леммой Эйлера о рукопожатиях (если несколько человек обменялись рукопожатием, то число пожатых рук – четно). Из этой леммы следует, что

В любом графе число вершин нечетной степени всегда четно.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

Доказательство леммы. Заметим, что сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной. Это следует из того, что если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю. Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы. Таким образом, сумма всех степеней вершин четна. Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной. Это значит, что само число таких вершин должно быть четным. Лемма доказана.

Д ва графа G1 и G2 называются изоморфными, если существует взаимно-однозначное соответствие между множествами их вершин, обладающее свойством, что число ребер, соединяющих любые две вершины в G1 равно числу ребер, соединяющих соответствующие вершины в G2

Изоморфизм графов

Графы на рис. 1.7 все выглядят как различные, но каждый из них можно перерисовать так, чтобы он стал (если не обращать внимание на обозначение вершин) идентичен другому. То есть все эти графы в некотором смысле "эквивалентны", имеют одинаковую структуру. Определим более точно характер этой "эквивалентности".

Рис. 1.7. Пример изоморфных графов

Графы G=(V,E) и G'=(V',E') изоморфны (пишут ), если существует взаимно-однозначное соответствие между множествами V и V', сохраняющее смежность вершин (т.е. такое соответствие, при котором вершины v_i и v_j из множества V смежны тогда и только тогда, когда смежны соответствующие им вершины и из множества V' ).

Изоморфизм графа рис. 1.7, к графу рис. 1.7, б обнаруживается, если задать следующее соответствие между вершинами: а1-б1, а2-б5, а3-б6, а4-б3, а5-б2, а6-б4. Изоморфизм графа рис. 1.7, к графу на рис. 1.7, а и рис.1.7, б предлагается установить читателю, определив надлежащее соответствие между их вершинами.

(а1,а4) (а1,а5) (а1,а6) == (б1,б3) (б1,б2) (б1,б4)

(а2,а4) (а2,а5) (а2,а6) == (б5,б3) (б5,б2) (б5,б4)

(а3,а4) (а3,а5) (а3,а6) == (б6,б3) (б6,б2) (б6,б4)