Лабораторная работа № 9 Трехфазные цепи с соединением нагрузки в треугольник

Цель работы – опытным путем установить соотношения между линейными и фазными величинами токов и напряжений, осуществить анализ работы нейтрального провода, освоить построение векторных диаграмм токов и напряжений для трехфазной цепи.

Общие сведения

Схемы соединений трехфазных цепей

Одним из способов соединения обмоток генератора с нагрузкой является соединения нагрузки треугольником.

При соединении обмоток генератора треугольником (рис. 9.1) конец первой обмотки генератора соединяют с началом второй, конец второй с началом третьей, конец третьей с началом первой. Геометрическая сумма эдс в замкнутом треугольнике равна нулю. Поэтому если к зажимам А, В, С не присоединена нагрузка, то по обмоткам генератора не будет протекать ток.

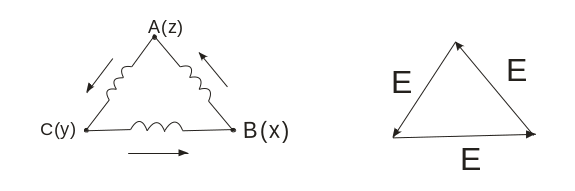
Рисунок 9.1 Соединение обмоток генератора треугольником

При этом следует отметить тот факт, что расположение векторов фазных эдс, соединенных звездой или треугольником, на комплексной плоскости, не следует связывать с расположением в пространстве осей трех обмоток генератора.

Приемники соединяются треугольником в том случае, когда номинальное эксплуатационное напряжение каждого приемника соответствует линейному напряжению источника, при этом три фазы приемника с фазными сопротивлениями Z_ав, Z_вс, Z_са включаются непосредственно между линейными проводами трехпроводной цепи.

Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным (будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой). Поэтому схема включения треугольником широко используется для включения несимметричной нагрузки.

Симметричная и несимметричная нагрузка

По рис 9.2 видно, что при соединении генератора в треугольник линейное напряжение равно фазовому напряжению генератора U_л=U_ф.

.

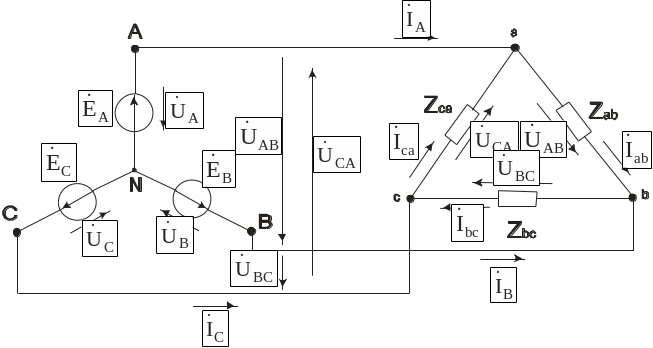Рис. 9.2 Соединение приемников треугольником

За положительное направление токов, при соединении нагрузки треугольником берут направление, совпадающее с направлением часовой стрелки. Индексы у токов соответствуют выбранным для них положительным направлениям: первый индекс отвечает точке, от которой ток утекает, второй – точке, к которой ток притекает.

При симметричной и несимметричной нагрузке фазные токи определяют по закону Ома: , но вследствие несимметрии нагрузки токи уже не образуют симметричную систему.

При соединении нагрузки треугольником линейные токи не равны фазовым токам нагрузки и определяются по первому закону Кирхгофа:

; .

Складывая левые и правые части последнего уравнения, получим: , т.е. геометрическая сумма линейных токов равна нулю.

При симметричной нагрузке фаз линейные токи по модулю в раз больше фазовых токов нагрузки: .

При несимметричной нагрузке линейные токи могут быть и больше и меньше фазовых токов нагрузки.

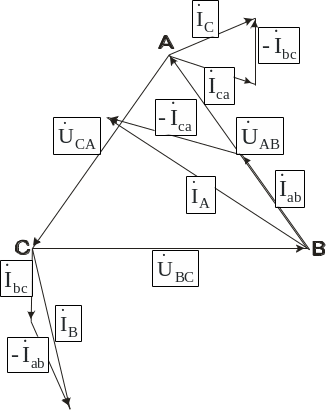
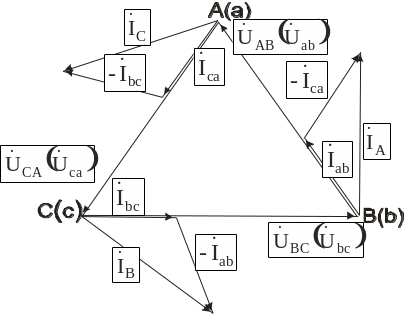
Пример построения векторной диаграммы токов и напряжений для симметричной активной нагрузки (Z_ав = Z_вс = Z_са = r) и не симметричной нагрузки Z_ав = r; Z_вс = +jx; Z_са = -jx приведен на рисунке 9.3.

Рисунок 9.3
а) векторная диаграмма токов и напряжений при несимметричной нагрузке; б) векторная диаграмма токов и напряжений при симметричной нагрузке.

 

Симметричные трехфазные приемники можно включать в трехпроводную цепь либо звездой, либо треугольником. Это значительно расширяет область применения таких приемников. Так, если на трехфазном электродвигателе указаны два напряжения 380/220 В и выведены концы и начала всех его обмоток, то его надо включить звездой, когда линейное напряжение сети U_л = 380 В и U_ф=220 В, и включить треугольником, когда линейное напряжение сети U_л = 220 В.

Определение мощности при соединении приемников треугольником

Мощности отдельных фаз находят по формулам:

, , .

Аналогично определяются активная и реактивная мощности двух других фаз.

Общая мощность трехфазной системы определяется арифметической или алгебраической суммой мощностей отдельных фаз:

_{, ,} .

При симметричной нагрузке мощности отдельных фаз равны между собой, следовательно

, , .

Учитывая, что при соединении в треугольник U_л = U_ф и I_л = I_ф, получим

; ; .

Таким образом, независимо от схемы соединения фаз приемника активная, реактивная и полная мощности при симметричной нагрузке определяются одними и теми же формулами.