Контрольные вопросы

1. Как определить полное и комплекс полного сопротивления цепи с последовательным соединением R, L, C-элементов. Чем они отличаются?

2. Чему равно реактивное сопротивление цепи?

3. Как рассчитать ток, в цепи с последовательным соединением R, L, C- элементов без применения и на базе комплексных чисел? Что должно быть задано в качестве исходных данных?

5. Какой режим называют резонансным? При каких условиях он возникает? Почему резонансный режим в цепи с последовательным соединением R, L, C-элементов называют резонансом напряжений, а не резонансом тока?

6. Может ли возникнуть резонансный режим при последовательном соединении резистора и конденсатора?

7. Как определить по показаниям приборов наступления резонанса напряжений?

8. По какой причине напряжение на реальной катушке индуктивности в резонансном режиме превышает напряжение на конденсаторе?

9. С какой целью применяют векторные диаграммы?

10. Чем отличаются векторная диаграмма токов и напряжений от треуголь­ника напряжений?

11 .Что означает коэффициент мощности цепи?

Лабораторная работа № 7 Параллельное соединение r, l, c элементов

Цель работы: провести анализ цепи, содержащей параллельное соединение R, L, С элементов, практически исследовать резонанс токов, изучить построение векторных диаграмм при разложении токов на составляющие.

Общие сведения

Пусть имеются три нагрузки (рис. 7.1). Первая нагрузка активно-индуктивная, вторая – активно-емкостная, третья – чисто активная, т.е. , , .

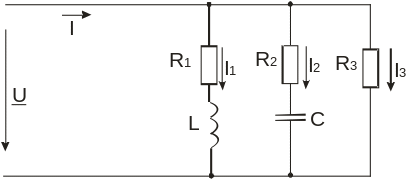
Рисунок 7.1. Параллельно включенные нагрузки

При параллельном включении нагрузок основным вектором является вектор напряжения, .

По первому закону Кирхгофа для мгновенных значений будет: . Для действующих значений: .

На рисунке 8.2 построена векторная диаграмма рассматриваемой цепи. Первый ток отстает от напряжения, т.к. первая ветвь цепи активно-индуктивная. Второй ток опережает напряжение на угол φ₂ и третий ток совпадает по фазе с напряжением.

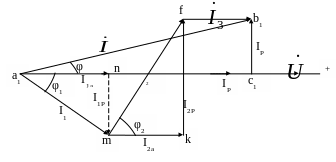
Рисунок 7.2 Векторная диаграмма цепи

При этом , .

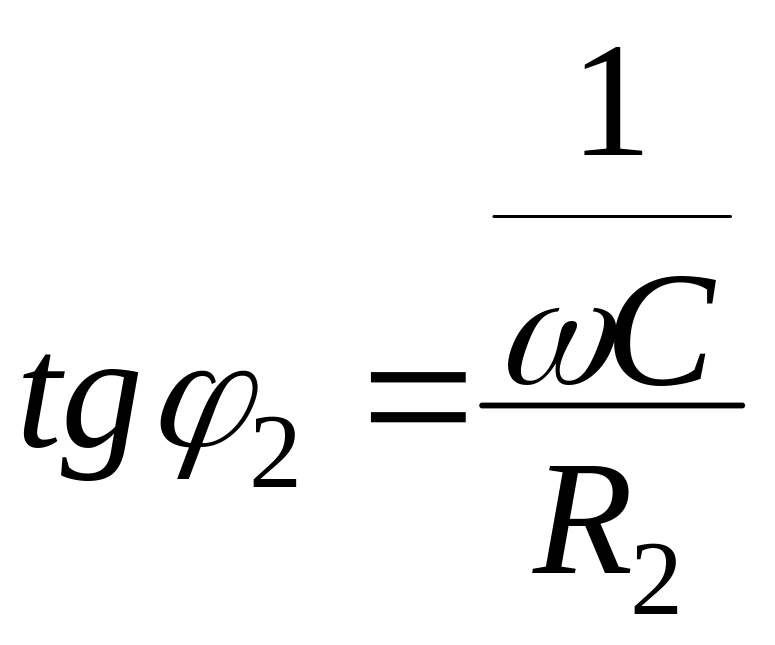Ток любой ветви, в том числе и общий ток, может быть разложен на активные и реактивные составляющие. На рисунке 7.2 треугольники а₁nm, mfk, а₁в₁с₁- треугольники токов. Общий ток:

. (а)

Рассмотрим в отдельности компоненты, составляющие выражение (а):

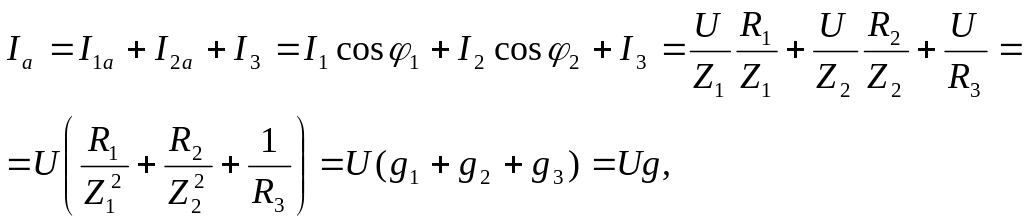(б)

где g₁, g₂, g₃, g- активные проводимости ветвей и всей цепи.

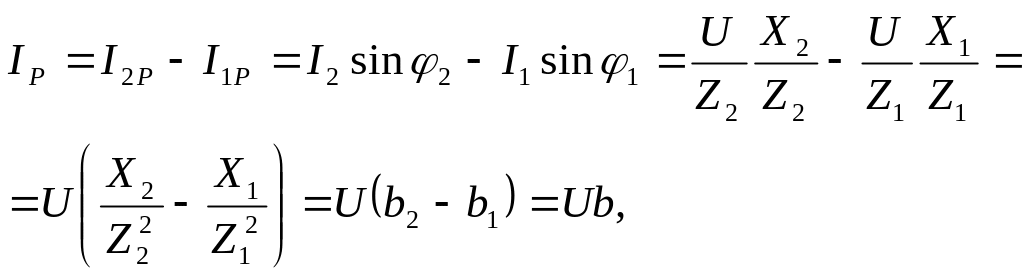(в)

где b₁, b₂ и b – реактивные проводимости ветвей и всей цепи.

Представим выражения (б) и (в) в выражение (а):

(7.1)

где Y – полная проводимость цепи.

На рисунке 7.3 представлен треугольник проводимостей, полученный из треугольника токов, поскольку .

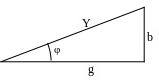
Рисунок 7.3 Треугольник проводимостей

Резонанс токов

Резонанс токов наступает при условии (рис.7.4) или , .

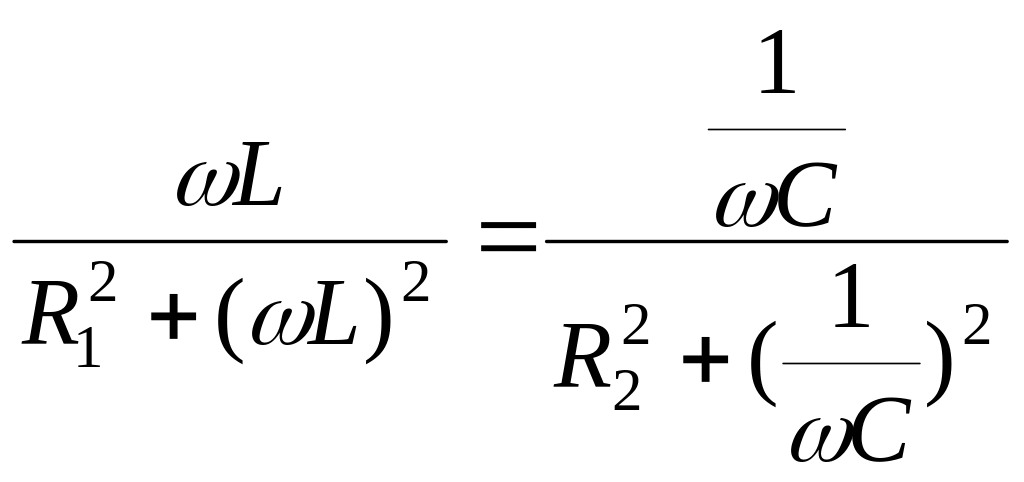Отсюда резонансная частота:

(7.2)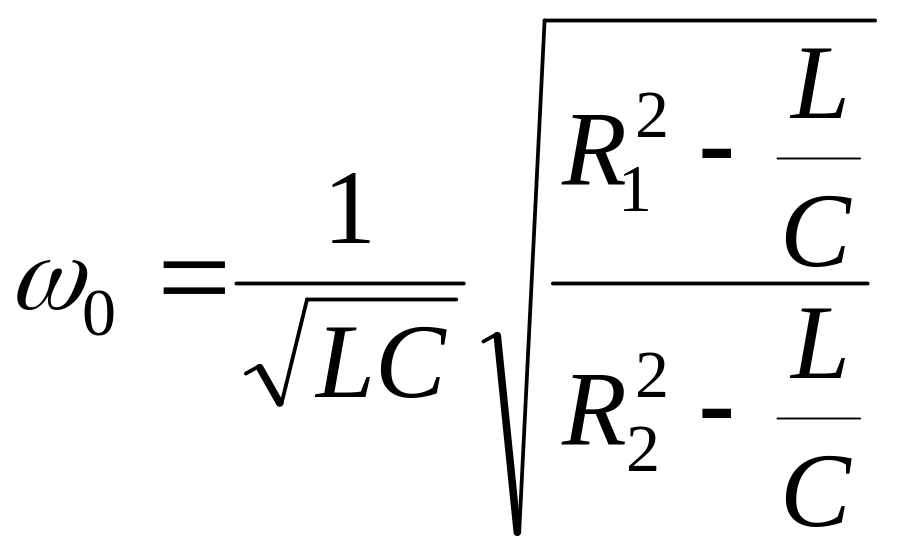

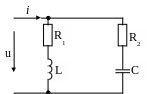
Рисунок 7.4 Цепь с параллельным включением нагрузок

В отличие от резонанса напряжений, резонансная частота резонанса токов зависит не только от L и С, но и от резисторов. Поэтому при R₁= R₂ или при их отсутствии (R₁= R₂=0) формула резонансной частоты для резонанса тока и резонанса напряжения одинакова.

Общий ток цепи: .

При резонансе ток имеет минимальное значение . При R₁=R₂=0 общий ток I=0, т.к. g=0.

Из векторной диаграммы токов (рис.7.5) можно показать, что ток на входе значительно меньше токов в ветви.

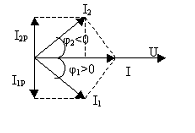
Рисунок 7.5 Векторная диаграмма

В теоретическом случае при r₁ = r₂ = 0, токи и сдвинуты по фазе относительно напряжения на и и ток на входе цепи . Входное сопротивление цепи при этом бесконечно велико. Если b_L=b_C и при

получим 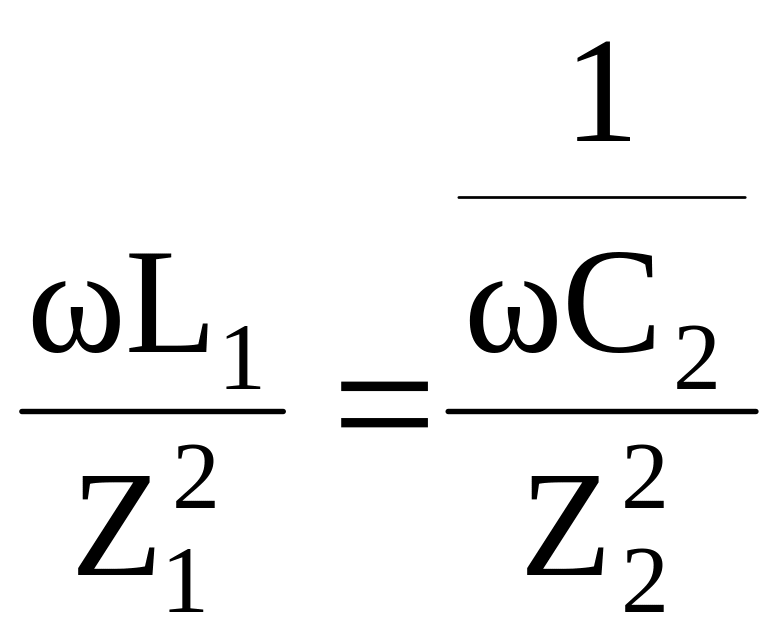или .

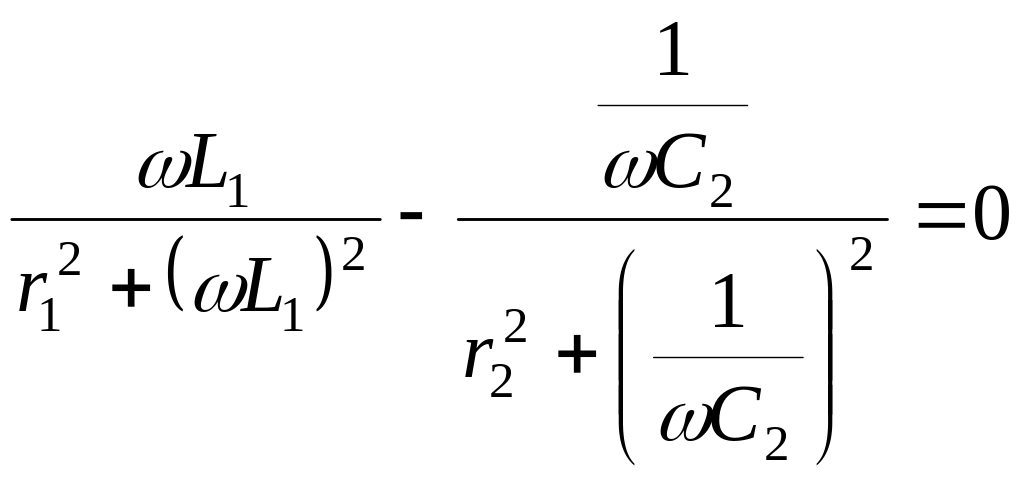Тогда резонанс можно достичь, изменяя либо частоту, либо параметры цепи (L₁, C₂, r₁, r₂). Решая уравнение относительно ω, получим следующее выражение для резонансной частоты

.

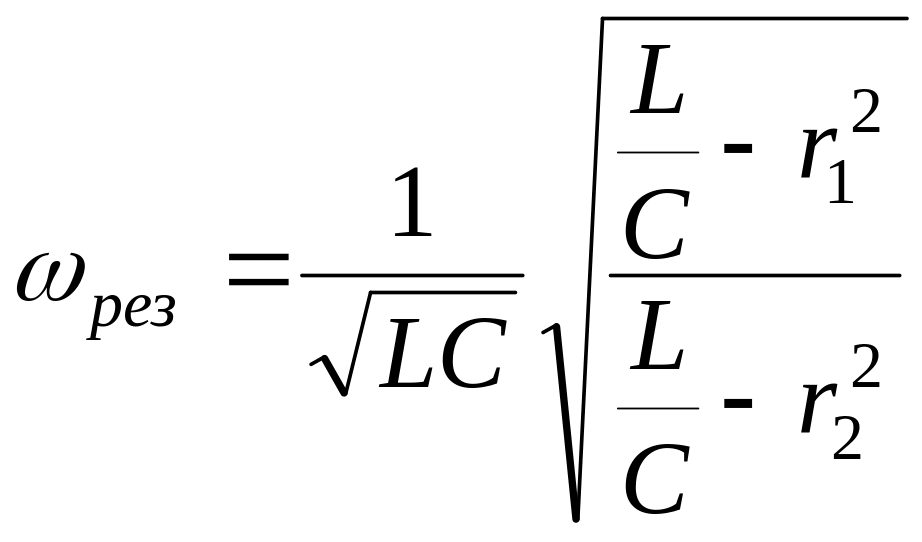Для получения резонанса необходимо соблюдение следующих условий:

1) При r₁ и r₂ оба больше либо оба меньше .

2) При r_1> и r_2< ω₀ - мнимое, не существует частоты, при которой был бы резонанс.

3) При r₁=r₂≠ , - формула частоты та же, что и при последовательном соединении.

4) Если r₁=r₂= , то , т. е. резонанс наблюдается при любой частоте.

При неизменной частоте источника питания, резонанс может быть получен путем изменения L₁,С₂, r₁, r₂.

Энергетические процессы, протекающие при резонансе токов при r₁=r₂=0, I=0, можно описать следующим образом:

- при r₁=r₂=0 поступление энергии в цепь не происходит;

- в цепи имеет место колебательный переход энергии из электрического поля в магнитное и наоборот.

При этом отметим, что если хотя бы одна из ветвей обладает активным сопротивлением, то и в цепь поступает энергия от источника питания. Тогда возврата энергии к источнику питания не наблюдается, т.к. ток совпадает по фазе с напряжением в момент времени t≥0.

В случае r₁=r₂= 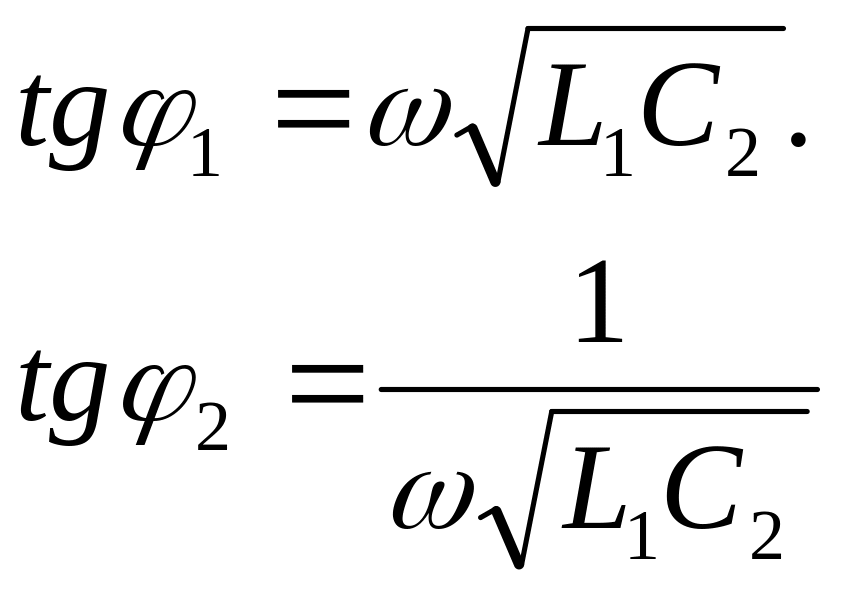, или .

Ток опережает по фазе ток на (рис.7.6).

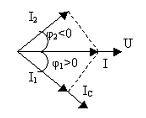
Рисунок 7.6

Напряжение , отстающее по фазе от тока на , оказывается в фазе с током в индуктивности . Таким образом, ток в индуктивности и напряжения на емкости одновременно проходит через нуль и максимум. Следовательно, энергия магнитного и электрических полей изменяется, совпадая по фазе, то есть одновременно достигая максимальных и нулевых значений. При этом колебания энергии между магнитным и электрическим полями совершенно отсутствуют. Когда абсолютные значения напряжения емкости U_C и тока в индуктивности i возрастают, энергия в электрическое и магнитное поле поступает от источника питания.

Исследуем частотные характеристики цепи с элементами r, L и С. Для нее резонанс наступает при частоте . При изменении частоты ω от нуля до ∞ графики I_r, I_L, I_C будут вида (рис. 7.7).

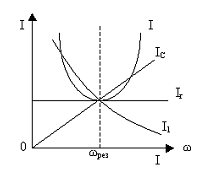
Рис.7.7

1.

2.

3. , где