- •Содержание
- •4. Методические указания к выполнению контрольной
- •Введение
- •Общие методические указания основные вопросы к экзамену за первый курс
- •Тема 1. Линейная алгебра и аналитическая геометрия
- •Тема 2. Дифференциальное исчисление функции одной независимой переменной
- •Тема 3. Дифференциальное исчисление функции одной переменной
- •Тема 4. Интегральное исчисление
- •Правило выбора варианта
- •Правила оформления контрольных работ
- •Контрольная работа 1
- •Тема 1. Аналитическая геометрия на плоскости Задачи 1–20
- •Тема 2. Элементы линейной алгебры Задачи 21–30
- •Тема 3. Введение в математический анализ Задачи 31–40
- •Тема 1. Дифференциальное исчисление функции одной переменной
- •Задачи 11– 20
- •Задачи 21– 30
- •Тема 2. Интегральное исчисление Задачи 31– 40
- •Задачи 41–50
- •К выполнению контрольной работы 1
- •Задачи 1-20 Аналитическая геометрия на плоскости
- •Пределы функций, основные теоремы о пределах
- •Замечательные пределы, эквивалентные бесконечно малые функции
- •Задачи 41– 50 Непрерывность функции
- •1. Правила дифференцирования.
- •2. Производная сложной функции.
- •3. Таблица производных.
- •Задачи 11 – 20 Исследование функции
- •Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график.
- •Задачи 31–40 Неопределенный интеграл, методы интегрирования
- •Задачи 41–50 Определенный интеграл, вычисление площадей
- •Справочный материал по элементарной математике
- •Графики основных элементарных функций
Правила оформления контрольных работ
При выполнении контрольных работ по математике нужно придерживаться следующих правил:
Каждую контрольную работу выполнять в отдельной тетради чернилами любого цвета, кроме красного и зеленого, оставляя поля для замечаний преподавателя.
На обложке тетради разборчиво написать фамилию, инициалы, номер контрольной работы, название дисциплины. В конце работы указать дату выполнения и расписаться.
Работа обязательно должна содержать все задачи именно вашего варианта.
Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
Перед решением каждой задачи записать полностью ее условие.
Решения задач излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
После получения проверенной работы следует исправить все отмеченные преподавателем ошибки и недочеты и выполнить все его рекомендации.
Контрольная работа 1
Тема 1. Аналитическая геометрия на плоскости Задачи 1–20
Даны вершины треугольника: А(х1; у1), В(х2; у2), С(х3, у3).
Сделать чертеж и найти:
длину стороны АВ;
внутренний угол при вершине А;
уравнение высоты, проведенной через вершину С;
уравнение медианы, проведенной через вершину В;
точку пересечения медианы ВЕ и высоты СD;
длину высоты, опущенной из вершины С.
1. А (-5; 0), |
В (7; 9), |
С (5; -5); |
2. А (-7;2), |
В (5; 11), |
С (3; -3); |
3. А (-5;-3), |
В (7; 6), |
С (5; -8); |
4. А (-6; -2), |
В (6; 7), |
С (4; -7); |
5. А (-8;-4), |
В (4; 5), |
С (2;-9); |
6. А (0; -1), |
В (12;8), |
С (10; -6); |
7. А (-6; 1), |
В (6; 10), |
С (4; -4); |
8. А (-2; -4), |
В (10; 5), |
С (8; -9); |
9. А (-3; 0), |
В (9;9), |
С (7; 5); |
10. А (-9; -2), |
В (3; 7), |
С (1; -7). |
11. А (-3; 3), |
В (9; -6), |
С (7; 8). |
12. А (-7; -1), |
В (-5; -10), |
С (3; 4). |
13. А (-4; 1), |
В (8; -8), |
С (6; 6). |
14. А (1; 2), |
В (13; -7), |
С (11; 7). |
15. А (-2; 2), |
В (10; -7), |
С (8; 7). |
16. А (-8; 4), |
В (4; -5), |
С (2; 9). |
17. А (0; 3), |
В (12; -6), |
С (10; 8). |
18. А (-7; 1), |
В (5; -8), |
С (3; 6). |
19. А (-7; 5), |
В (5; -4), |
С (3; 10). |
20. А (-5; 2), |
В (7; -7), |
С (5; 3). |
Тема 2. Элементы линейной алгебры Задачи 21–30
Решить систему линейных уравнений методом Крамера.
21.
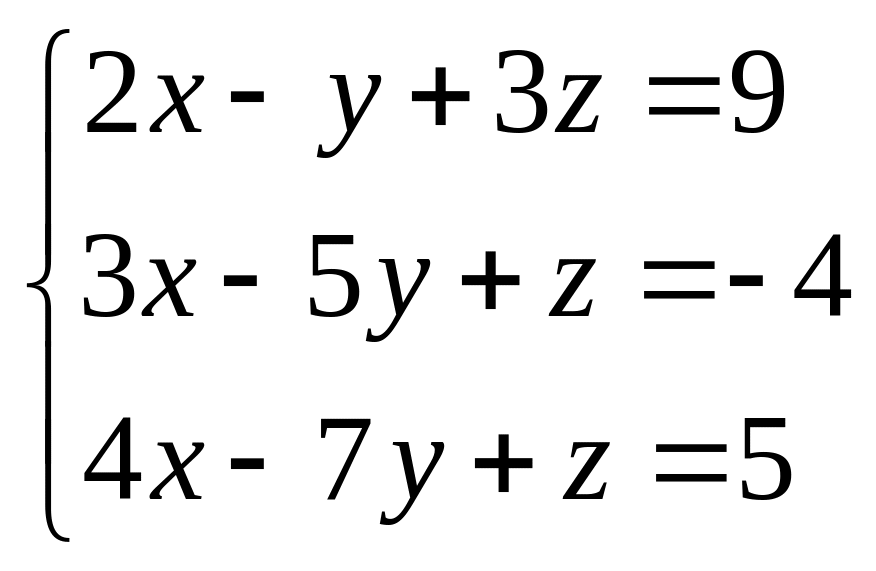 22.
22.
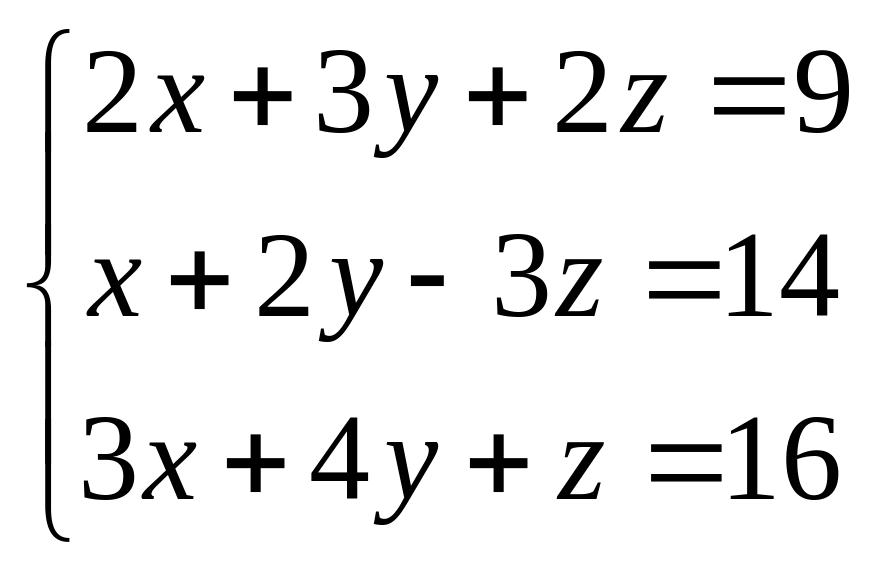 23.
23.
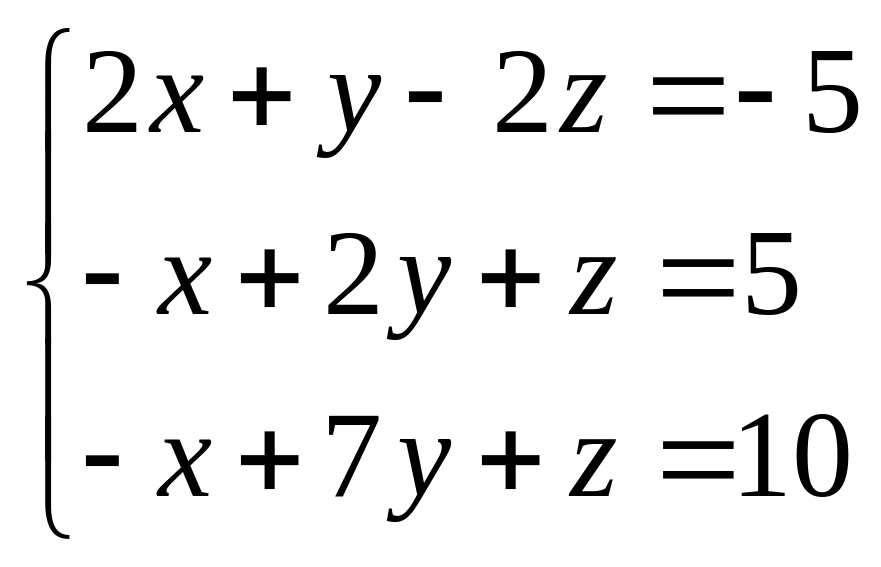
24.
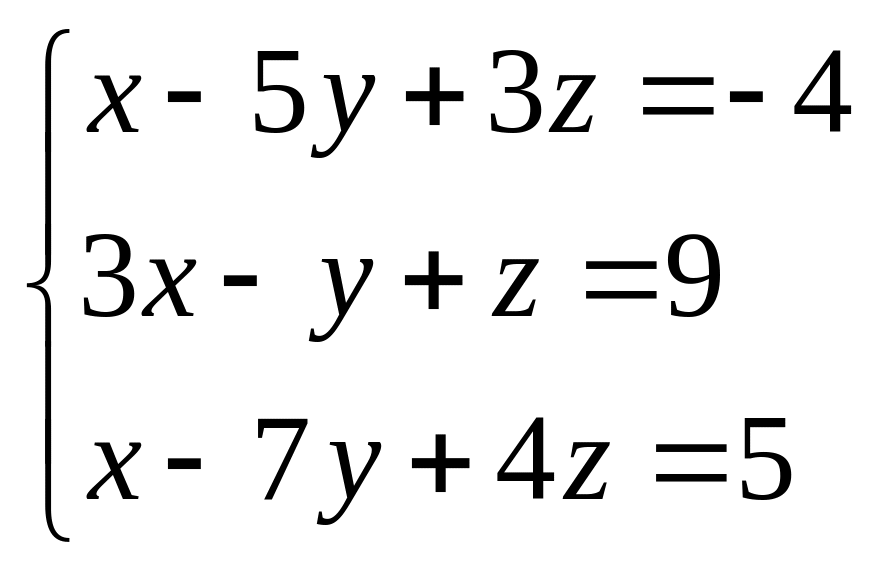 25.
25.
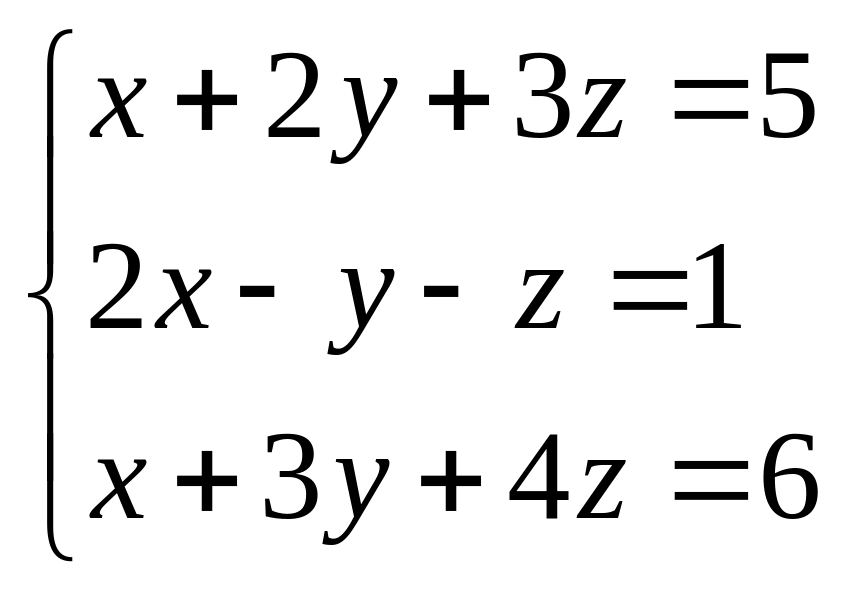 26.
26.
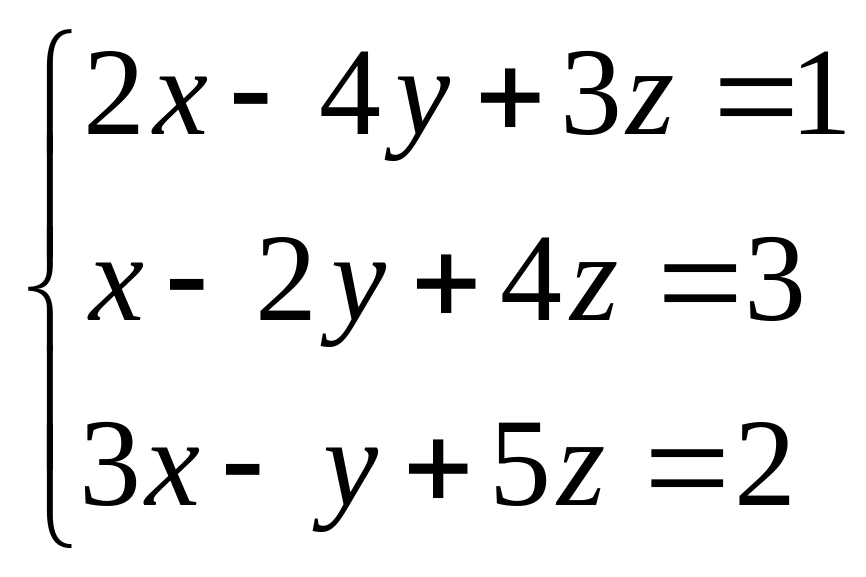
27.
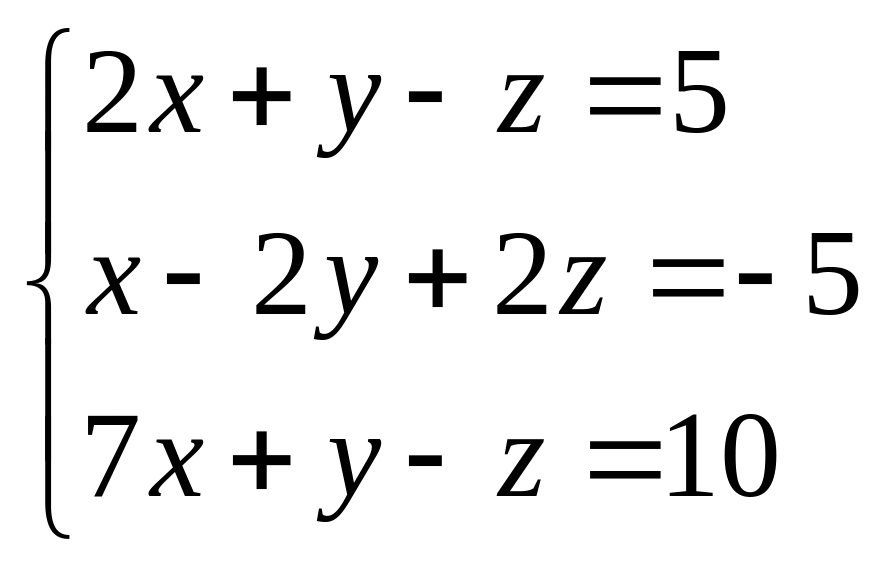 28.
28.
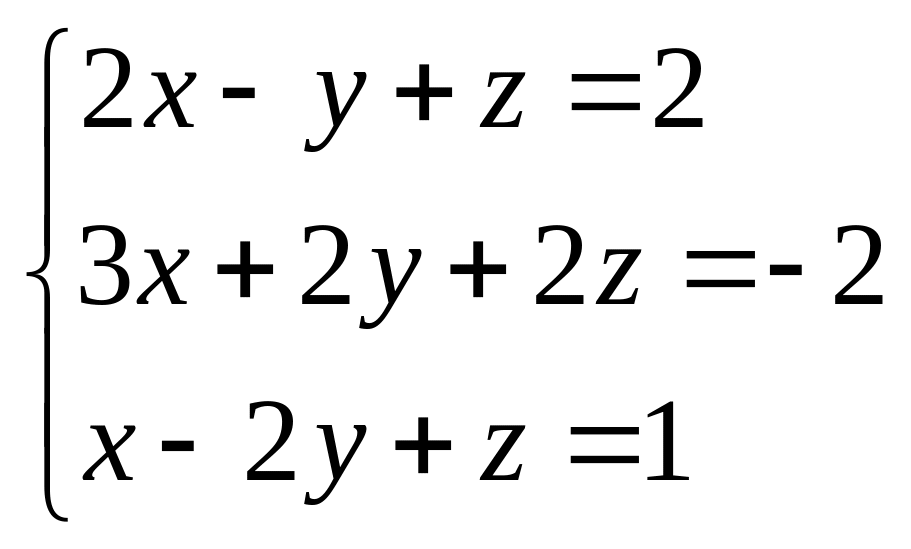 29.
29.
30.