
- •Міністерство освіти і науки національний університет водного господарства та природокористування Математичні методи і моделі
- •Основні теоретичні відомості Постановка завдання інтерполяції
- •Розділені різниці. Інтерполяційний багаточлен Ньютона.
- •Похибка інтерполяції
- •Інтерполяційні формули Ньютона у разі рівновіддалених вузлів
- •Зразок виконання лабораторної роботи
- •Література
Міністерство освіти і науки національний університет водного господарства та природокористування Математичні методи і моделі
Методичні вказівки до лабораторних занять № 6 для студентів для напряму підготовки 6.080101 ,,Геодезія, картографія та землеустрій”
Рівне–2013
УДК 378+004
ББК 32. 973
Т 47
Математичні методи і моделі. Методичні вказівки до лабораторних занять № 6 для студентів для напряму підготовки 6.080101 ,,Геодезія, картографія та землеустрій” – Рівне: НУВГП, 2013. – 12 с.
Укладач: Ю.Й. Тулашвілі
Рецензенти:
Відповідальний за випуск: Ю.Й. Тулашвілі
Рекомендовано методичною комісією за галуззю знань 0403 "Системні науки та кібернетика", протокол № від 2013 року.
© Ю.Й. Тулашвілі 2013
Основні теоретичні відомості Постановка завдання інтерполяції
Нехай
на відрізку [a, b] задані n+1 точки
![]() ,
які називаються вузлами інтерполяції,
і значення деякої функції
,
які називаються вузлами інтерполяції,
і значення деякої функції
![]() в цих точках
в цих точках
![]() .
Треба побудувати функцію
.
Треба побудувати функцію
![]() (інтерполююча функція), що належить
відомому класу і що має у вузлах
інтерполяції ті ж значення, що і
,
тобто таку, що
(інтерполююча функція), що належить
відомому класу і що має у вузлах
інтерполяції ті ж значення, що і
,
тобто таку, що
![]() .
.
Геометрично
це означає, що треба знайти криву
![]() деякого певного типу, що проходить через
задану систему точок
деякого певного типу, що проходить через
задану систему точок
![]() .
.
Отриману інтерполяційну формулу зазвичай використовують для наближеного обчислення значень певної функції для значень аргументу х, відмінних від вузлів інтерполяції. Така операція називається інтерполяцією функції .
У такій
загальній постановці завдання може
мати незліченну безліч рішень або зовсім
не мати їх. Проте це завдання стає
однозначним, якщо замість довільної
функції
шукати поліном
![]() із степенем не вище
із степенем не вище
![]() ,
що задовольняє умовам (1), тобто такий,
що
,
що задовольняє умовам (1), тобто такий,
що
![]() .
.
Інтерполяційний багаточлен Лагранжа
Якщо
вузли
![]() різні, то існує єдиний інтерполяційний
багаточлен
із степенем
.
Його можна записувати в різних формах.
Розглянемо інтерполяційний багаточлен
Лагранжа і Ньютона. У формі Лагранжа
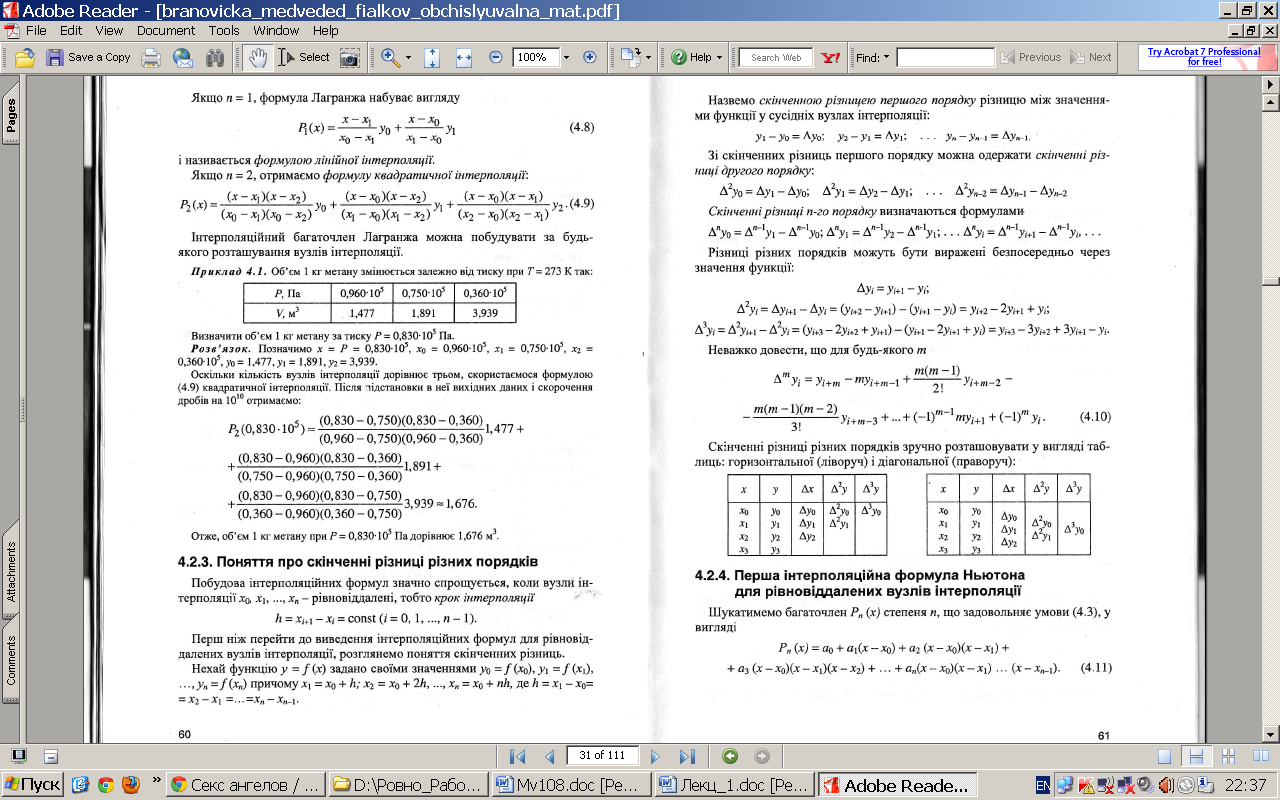
інтерполяційний багаточлен
має вигляд
різні, то існує єдиний інтерполяційний
багаточлен
із степенем
.
Його можна записувати в різних формах.
Розглянемо інтерполяційний багаточлен
Лагранжа і Ньютона. У формі Лагранжа
інтерполяційний багаточлен
має вигляд
 (1)
(1)
Наприклад,
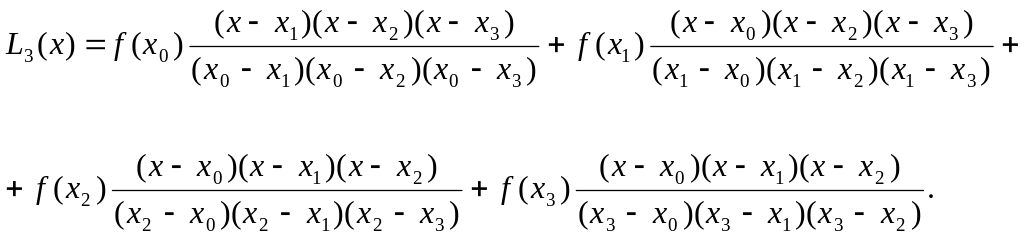
Розділені різниці. Інтерполяційний багаточлен Ньютона.
Щоб
ознайомитися з інтерполяційним
багаточленом у формі Ньютона, введемо
в розгляд поняття розділена різниця.
Значення
![]() функції
у вузлах називаються розділеними
різницями нульового порядку. Числа виду
функції
у вузлах називаються розділеними
різницями нульового порядку. Числа виду
![]() називаються розділеними різницями
першого порядку.
називаються розділеними різницями
першого порядку.
Розділена
різниця
-го
порядку визначається через розділені
різниці
![]() -го
порядку по реккурентной формулі
-го
порядку по реккурентной формулі
![]() .
.
Розділену
різницю
![]() -го
порядку (
-го
порядку (![]() )
можна виразити через
)
можна виразити через
![]() по наступній формулі:
по наступній формулі:
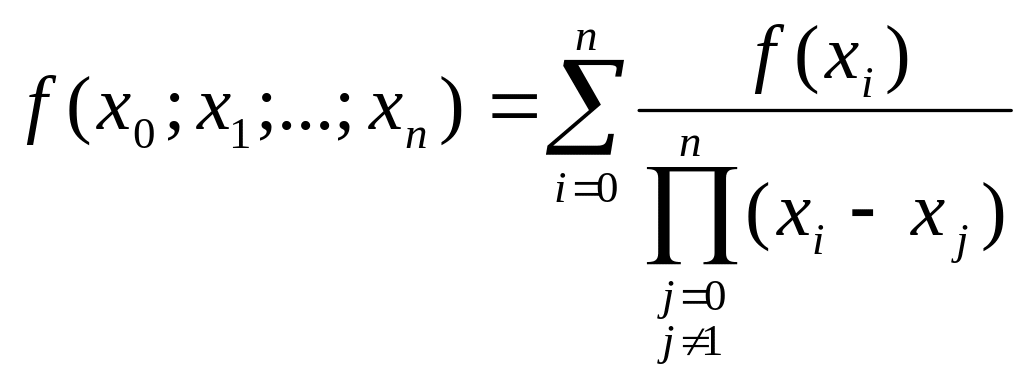 .
.
Наприклад,
![]() .
.
Тобто, розділена різниця - симетрична функція своїх аргументів. За допомогою розділених різниць інтерполяційний багаточлен у формі Ньютона можна записати таким чином:
![]() (2)
(2)
