2.2 Оцифровка

Иногда мультимедийные данные уже появляются в цифровом виде, как это происходит при создании изображений с помощью программ для рисования, но чаще приходится выполнять преобразование какого-то аналогового представления в цифровое, например, путем сканирования изображения.

Банальной иллюстрацией разницы между аналоговым и цифровым представлением может служить определение времени по современным часам (маятниковые часы и цифровой будильник (рис. 2.2)). Минутная стрелка маятниковых часов движется постоянно и может указывать на любую точку циферблата. В отличие от этого цифровой будильник может показывать только целые числа, обозначающие минут, а изображение на дисплее меняется только через каждые 60 секунд. Для точных расчетов цифровое представление удобнее, чем аналоговое; например, чтобы узнать, сколько времени осталось до половины первого, нужно просто отнять время изображенное на дисплее будильника, от 12:30, когда как в случае с аналоговыми часами придется оценивать разницу, основываясь на разнице углов между текущим положением часовой стрелки и ее положением посередине между 12 и часом.

Маятниковые часы	Электронные часы
Рис. 2.2

В мультимедийных средствах мы встречаемся со значениями, которые изменяются непрерывно несколькими способами. Например, амплитуда звуковой волны непрерывно изменяется во времени, как и амплитуда электрического сигнала, вырабатываемого микрофоном в ответ на действие звуковой волны. Яркость в любой точке черно-белой фотографии, в принципе, может иметь любое значение, хотя на практике существуют ограничения, накладываемые физическими возможностями самого процесса фотографирования. Как видно, мы можем измерять различные величины, и они могут изменяться либо во времени, либо в пространстве. При таких общих соображениях мы будем называть значения, которые мы измеряем, сигналом.

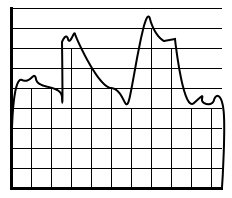
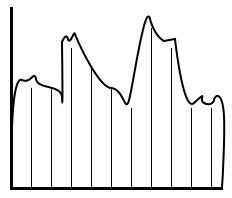
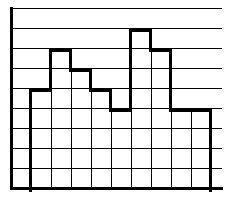
Когда у нас есть непрерывно изменяющийся сигнал, значение, которое мы измеряем, и интервал, на котором мы можем его измерять, могут изменяться на бесконечно малую величину. В отличие от этого, если бы нужно было преобразовать его в цифровой сигнал, то в обоих случаях (величина, интервал) пришлось бы ограничиться набором дискретных значений. Иначе говоря, оцифровка – а именно так называется процесс преобразования аналогового сигнала в цифровой – состоит из двух этапов: дискретизации, когда мы измеряем величину сигнала на определенных дискретных промежутках, и квантования, когда эти значения ограничиваются определенным набором уровней (рис. 2.3.1).

Дискретизация и квантование могут выполняться в произвольном порядке. Эти процессы выполняются специальными устройствами, которые обобщенно называются аналого- цифровыми преобразователями (АЦП). Количество элементов выборки на фиксированном отрезке времени или пространства называется частотой дискретизации. Точно так в общем случае мы будем считать, что уровни, на которые квантуется сигнал (уровни квантования), находятся на одинаковом расстоянии один от другого, хотя на практике встречается и иное расположение.

Рис. 2.3.1 Дискретизация и квантование

Одно из величайших преимуществ, которые имеет цифровое представление перед аналоговым, следует из того факта, что корректным являются только определенные значения сигнала – те, которые попадают на уровни квантования. Если сигнал передается по проводам или записывается на физический носитель, например на магнитную ленту, на него неизбежно накладываются случайные шумы, возникающие либо из-за влияния рассеянных магнитных полей, либо из-за неустранимых флуктуаций тепловой энергии самой проводящей среды. Эти шумы приводят к изменению значений сигнала. Если сигнал аналоговый, то шумы могут оказаться в большей или меньшей степени недетектируемыми: допускаются любые аналоговые значения, поэтому сигнал, загрязненный шумами, невозможно отличить от чистого сигнала. Но если сигнал цифровой, то любые незначительные флуктуации, вызванные шумом, как правило, переводят допустимые значения в разряд недопустимых, которые находятся между уровнями квантования. После этого очень легко восстановить исходный сигнал, проквантовав его еще раз. Ошибки могут при передаче могут возникать только тогда, когда шумы достаточно большие и, приводя к такому изменению сигнала, что его значение попадает на другой уровень. Но даже в таких случаях, благодаря тому, что сигналы можно описывать численно, можно придумать и реализовать схемы, которые находят и исправляют ошибки, используя для этого арифметические свойства групп битов. Следовательно, цифровые сигналы намного устойчивее, чем аналоговые, и не искажаются при копировании или передаче через зашумленную среду.

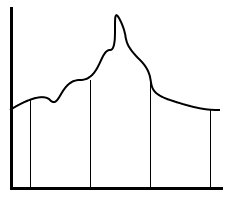
Если посмотреть на рисунки 2.3.1, можно увидеть, что в процессе оцифровки часть информации теряется. Единственной имеющей значение мерой точности должно быть то, насколько близко к оригиналу может быть восстановлен сигнал. Для того чтобы восстановить аналоговый сигнал по набору дискретных значений, все, что нужно сделать, – это решить, чем заполнить промежутки между этими точками. Можно точно описать процесс восстановления сигнала с помощью математических выражений, и такое описание даст точное представление о наилучшем, с теоретической точки зрения, способе построения искомого сигнала. На практике же используются более простые методы, которые намного легче реализовать с помощью более быстродействующего оборудования.

Рис. 2.3.2 Восстановление методом выборки-хранения (слева); Дискретизация с недостаточной частотой (справа)

Один из возможных способов – использование метода выборки-хранения (дискретизации с задержкой) (рис. 2.3.2), заключающего в следующем: значение в точке выборки остается постоянным на всем интервале между этой точкой и точкой, следующей за ней. Как показано на рисунке, это дает сигнал с резкими переходами, что в действительности является не очень хорошей аппроксимацией оригинала. Однако, когда сигнал с целью его изображения или прослушивания подается на такое устройство вывода, как экран электронно-лучевой трубки или громкоговоритель, задержки и изъяны, которые свойственны любым физическим приборам, приводят к тому, что резкие переходы сглаживаются, и в результате получается достаточно хорошая, с теоретической точки зрения, аппроксимация.

Хотя понятно, что если дискретные значения исходного сигнала находятся слишком далеко одно от другого, любое восстановление будет неадекватным, поскольку аналоговый сигнал может содержать такие детали, которые упускаются в процессе дискретизации из-за больших расстояний между элементами выборки. Один из таких случаев показан на рисунке 2.3.2 (справа): значения, взятые в соседних точках, одинаковы, и нельзя сделать вывод о присутствии пика между этими двумя точками – сигнал с такой же вероятностью может образовывать минимум или оставаться на том же уровне. Влияние такой дискретизации с недостаточной частотой на способ восстановления сигнала будет оцениваться в зависимости оттого, что собой представляет этот сигнал (звук, изображение и т.п.), и от того, изменяется ли он во времени или в пространстве.

Достаточно легко показать, что если частота дискретизации слишком мала, в процессе дискретизации некоторые детали будут утрачены. Немного сложнее определить, существует ли такая частота, при которой можно быть уверенным, что элементы выборки расположены достаточно близко один к другому, позволяя восстановить сигнал точно, а если она существует, то какого приближения будет достаточно. Чтобы лучше разобраться в подобных вопросах, нам придется рассмотреть альтернативный способ представления сигнала.

Вы наверняка знаете, что любая нота, которую можно сыграть на музыкальном инструменте, состоит из волн нескольких различных частот, сложенных вместе. Есть основной тон, высота которого ассоциируется с этой нотой, но, в зависимости от выбранного инструмента, присутствует также различное число гармоник, мили обертонов, и они придают ноте характерный тембр. Основной тон и каждая гармоника – это чистые звуки, синусоидальные волны одной частоты. Аналогичным образом любую периодическую волну можно разложить на набор составляющих с разными частотами, каждая из которых будет представлять собой правильную синусоиду (частота – это количество повторений сигнала в единицу времени). Если рассматривать сигналы, которые периодически изменяются в пространстве (рисунок периодические колебания яркости) (рис. 2.4.1), то для них частота будет иметь точно такой же смысл (количество повторений сигнала на единицу расстояния) (рис. 2.4.2). Следовательно, в общих рассуждениях частоты, равно как и сигналы, могут быть либо временными, либо пространственными.

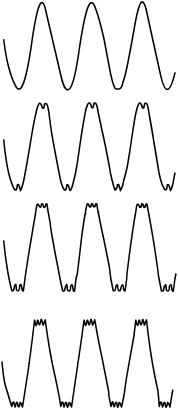
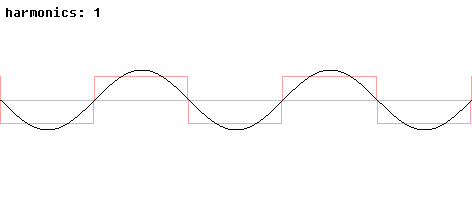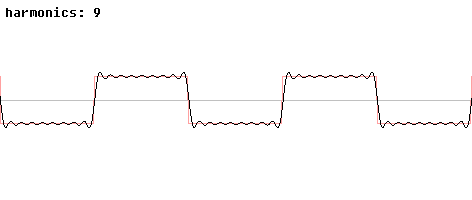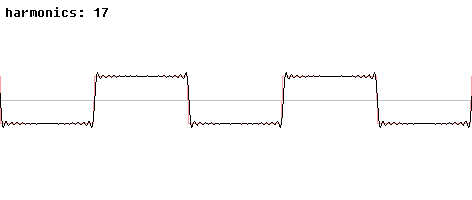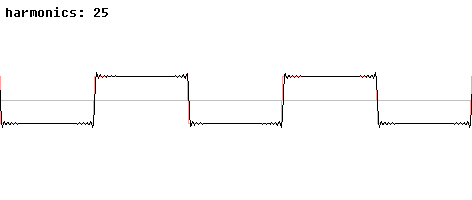
На рисунке (рис. 2.4.1, 2.4.2) приведен один из классических примеров того, как сочетания чистых синусоидальных волн с различными частотами дают более сложные волны. Начиная с чистой синусоидальной волны с частотой f, мы будем по очереди прибавлять к ней компоненты с частотами 3f, 5f, 7f и т.д., амплитуды которых равны одной третьей, одной пятой, одной седьмой значения амплитуды и так далее до значения амплитуды исходного сигнала. Как видно, чем больше «гармоник» мы добавляем, тем больше сигнал становится похожим на меандр¹ (прямоугольные колебание). Чем больше частотных компонентов мы прибавим, тем лучший будет аппроксимация.

Рис. 2.4.1 Периодические колебания яркости	Рис. 2.4.2 Частотные компоненты меандра

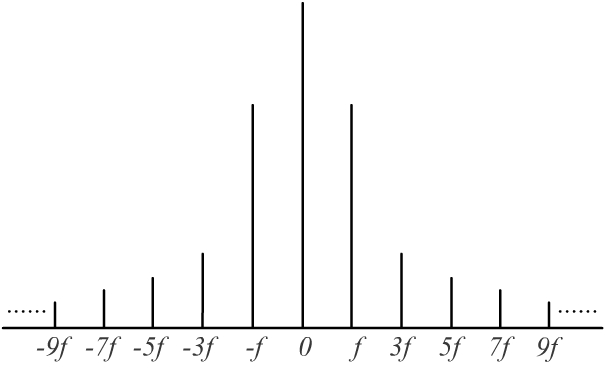
Для описания нашего сигнала можно было бы воспользоваться частотами и амплитудами его составляющих, хотя это и не обеспечивается такой же непосредственной прозрачности. Набор частот и амплитуд является представлением сигнала в частотной области (строго говоря, нужно знать еще и фазу компонента, поскольку иногда это необходимо для правильного их расположения один относительно другого). Его можно найти с помощью математической операции, известной под названием преобразование Фурье. Результат применения преобразования Фурье к сигналу (его Фурье-образ) можно изобразить, как и сам исходный сигнал, в виде графика, на котором по горизонтальной оси откладывается частота, а по вертикальной – амплитуда. Типичный частотный спектр сигнала, как называется такое представление, будет состоять из набора пиков на разных частотах, соответствующих различным компонентам. На рисунке 2.4.3б представлен наш меандр в частотной области. Как видно из рисунка, существуют и отрицательные частоты, это связано со смещением фазы, если смещение отсутствует, то представление будет симметричным. Существует также пик с нулевой частотой, который называется постоянной составляющей. Эта составляющая равна интегралу от всего сигнала и является мерой его среднего значения.

а)	б)
2.4.3 а) Меандр; б) Представление меандра в частотной области

На примере меандра можно продемонстрировать явление, которое имеет место для всех сигналов: высокочастотные компоненты связаны с резкими переходами. При добавлении компонентов с большей частотой передний и задний фронты импульса становятся почти вертикальными. Если посмотреть на это с другой стороны, устранив высокочастотные компоненты, подобные резкие переходы можно сгладить. Следовательно, такие операции, как увеличение резкости и сглаживание изображения, можно описывать и выполнять с помощью фильтров, которые устраняют определенные частоты; данный факт имеет фундаментальное значение в сфере обработке графической информации.

Обратное преобразование Фурье переводит сигнал из частотной области во временную.

Согласно теореме о дискретном представлении, если самая высокая частота из частот компонентов сигнала равна fh, то сигнал можно будет точно восстановить в том случае, если его дискретизация была выполнена с частотой, превышающей 2fh. Это граничное значение известно под названием частота Найквиста (этим термином мы будем называть самую низкую частоту дискретизации, необходимую для восстановления сигнала).

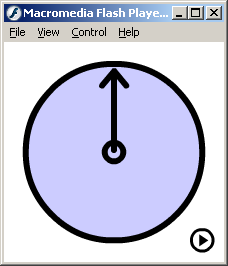
Доказательством теоремы о дискретном представлении достаточно формально, но суть самого явления, лежащего в ее основе, можно очень просто проиллюстрировать. Предположим, имеется круглый диск с одной отметкой, обозначающий радиус, который вращается по часовой стрелке со скоростью n оборотов в секунду. Предположим также, что это вращение «дискретизируется» с помощью кинокамеры, когда через одинаковые промежутки времени делаются моментальные снимки этого диска. На рисунке 2.5 показаны снимки, которые можно было бы получить при частоте дискретизации 4n раз в секунду.

n	4n	4/3n	2n
Рис. 2.5 Flash-ролик вращающейся стрелки дискретизированный с разной частотой n. (для просмотра щелкните на кнопку пуск)

Посмотрев на эту последовательность, можно увидеть, что диск вращается в направлении по часовой стрелки, и представить, что если бы эти изображения были бы кадрами фильма, следующими один за другим, мы увидели, что при прокручивании пленки диск вращается в правильном направлении. Если рассматривать вращающийся диск, как периодический сигнал, то его частота будет равна n, а дискретизация будет выполняться с частотой 4n, которая больше частоты Найквиста, что как раз нам подходит. А теперь посмотрим, что произойдет, если выполнять дискретизацию с частотой 4n/3. При взгляде на последовательность, состоящую только из этих элементов, по последовательным положениям линии кажется, что диск, скорее всего, вращается против часовой стрелки со скоростью n/3. Частота дискретизации должна превышать частоту Найквиста: если выполнять дискретизацию движения нашего диска с частотой, равной 2n, можно получить элементы, на которых линия будет находиться в одном из двух направлениях – либо верх, либо вниз, так что определить в каком направлении вращается диск, будет вообще невозможно.

В общем случае, если выполнять дискретизацию сигнала с недостаточной частотой, в процессе восстановления одни частотные компоненты исходного сигнала могут преобразовываться в другие частоты, точно так, как изменяется частота вращения нашего диска при дискретизации с недостаточной частотой. Это явление известно под названием наложение спектров и в различных средствах передачи информации проявляется по-разному. При записи звука оно слышится, как искажение; на изображениях оно, как правило, проявляется в виде зубчатых краев или, если изображение состоит из мелких повторяющихся деталей, в виде муарных картин; в случае времени приводит к прерывистым движениям, а также к явлениями, аналогичным описанному выше вращению диска в обратную сторону.

Как правило, влияние недостаточного количества уровней квантования интуитивно понять легче, чем эффект неподходящей частоты дискретизации. Если мы можем задать только ограниченное число различных значений, мы не сможем различать те значения, которые находятся между ними. В случае изображений это происходит так, как если бы мы были вынуждены обходиться лишь несколькими различными цветами, и поэтому пришлось бы пользоваться, скажем, ярко-красным цветом для обозначения любого необходимого нам оттенка красного цвета. Разница между алым и карминным цветами была бы утрачена, а любые границы между областями, заполненными этими цветами, исчезли бы. Этот эффект хорошо виден на черно-белых изображениях на рисунке 2.6, на котором показаны градиенты с уровнями яркости 256, 128, 64, 8, 4, 2. Первый градиент демонстрирует постепенный переход от чистого белого цвета к чистому черному, а затем видно, как при уменьшении количества уровней яркости соседние значения сливаются, поскольку их квантование становится все более и более грубым. Для не таких правильных изображений этот эффект проявляется в виде огрубления, или так называемым оконтуривание по яркости, когда цветные области сливаются, как на дешевых печатных плакатах. На рисунке 2.7 показано, как огрубление проявляется на печатном изображении: слева изображена цифровая фотография с миллионом оттенков, а справа она сведена до четырех.

256	128	8	4	2
Рис. 2.6 Черно-белые изображения с различными уровнями яркости

Рис. 2.7 Слева изображена цифровая фотография с миллионом оттенков, а справа та же фотография с четырьмя оттенками

Самой распространенной причиной ограничения количества уровней квантования является уменьшения объема памяти, необходимого для записи цифровой информации, путем ограничения количества битов, которые используются для записи каждого значения.