
- •Математика Методическое пособие для студентов
- •Часть 3
- •Математический анализ Программа курса
- •Контрольное задание
- •Теория вероятностей Программа курса
- •Случайные события и процессы.
- •Случайные величины.
- •Контрольное задание Вариант №1
- •Вариант №2
- •Вариант №3
- •Вариант №4
- •Вариант №5
- •Вариант №6
- •Вариант №7
- •Вариант №8
- •Вариант №9
- •Вариант №10
Контрольное задание
Вариант № 1
Вычислить
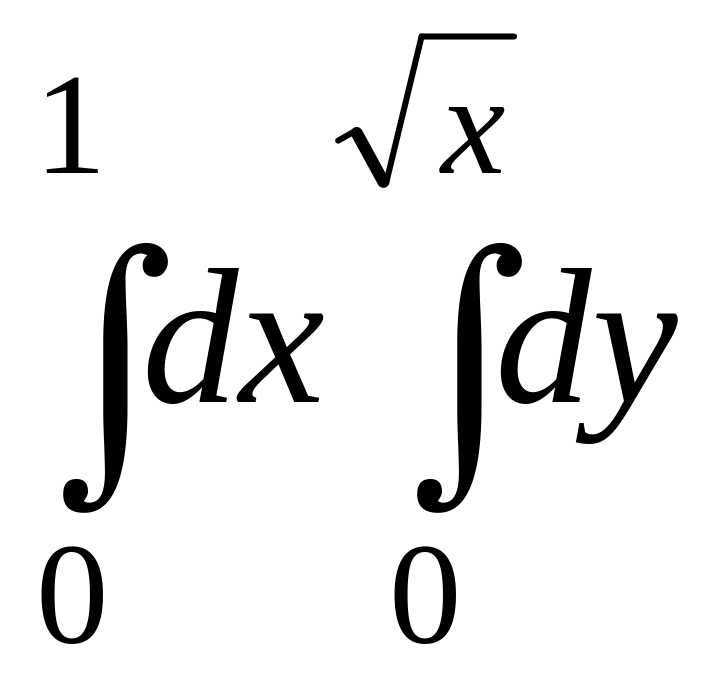
Вычислить
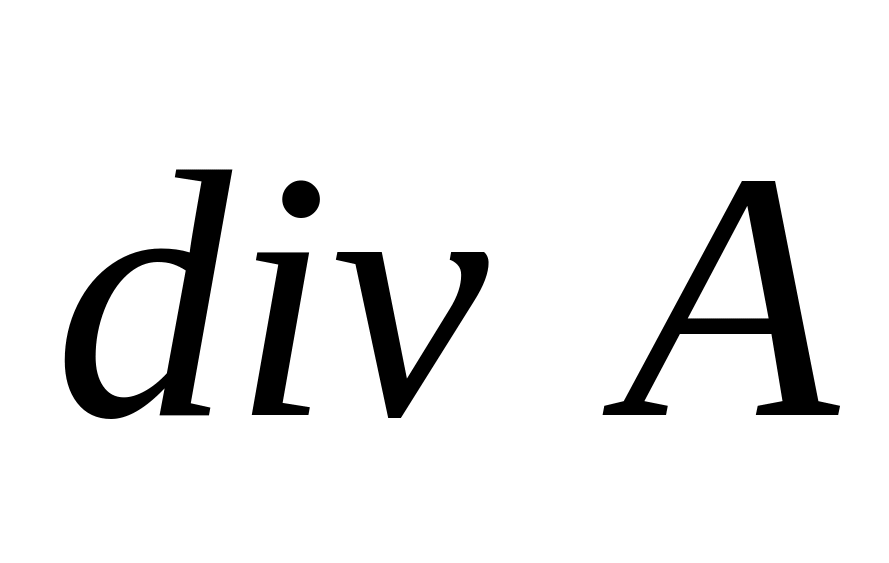 ,
если
,
если
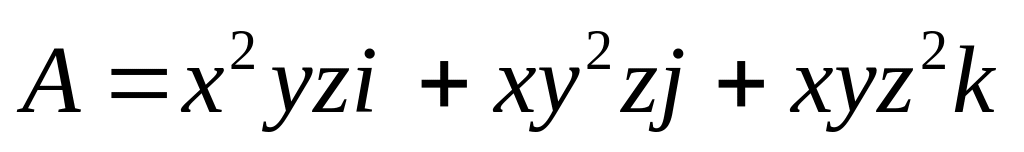 .
.Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
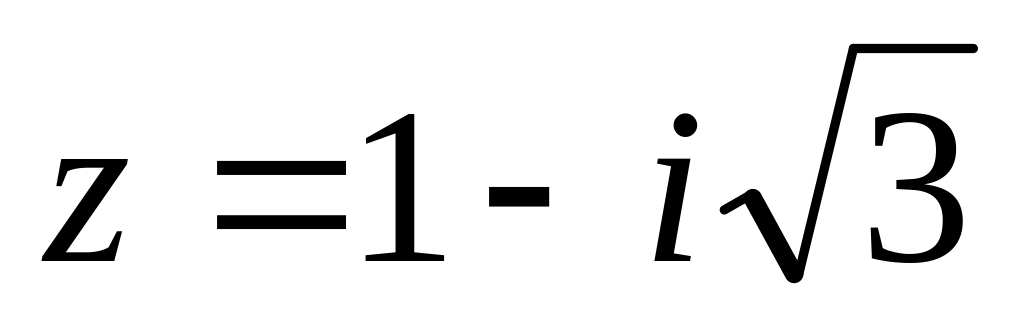 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
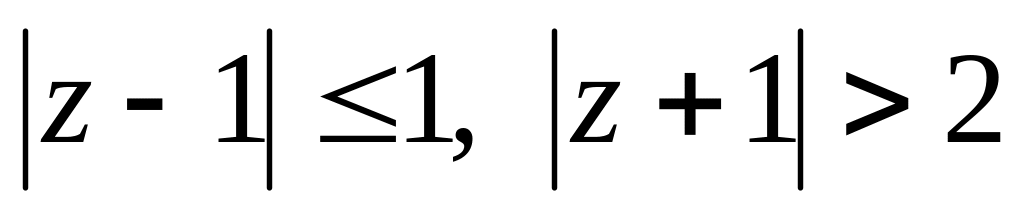 .
.
Вариант № 2
Вычислить
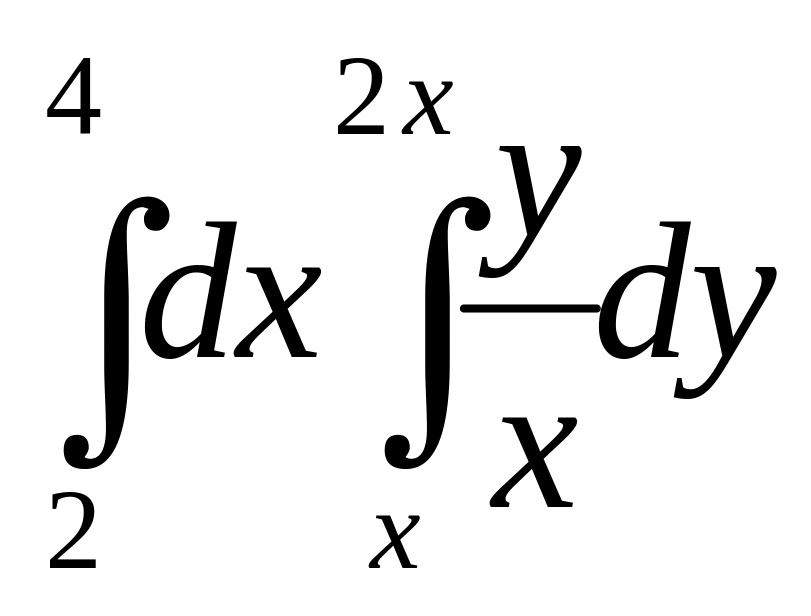
Вычислить
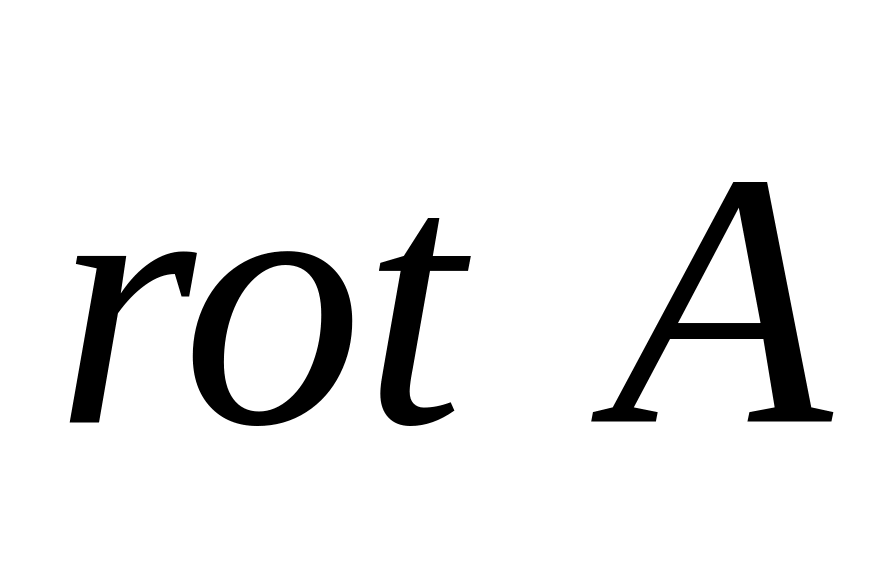 ,
если
,
если
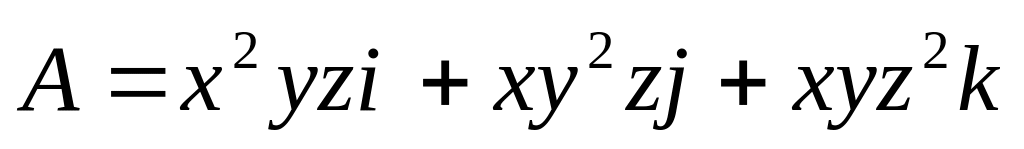 .
.Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа а) z=6i, б) z=5 и записать его в показательной форме.
Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
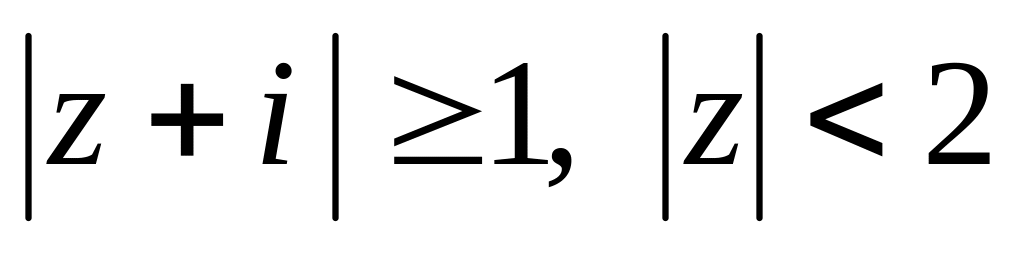 .
.
Вариант № 3
Вычислить
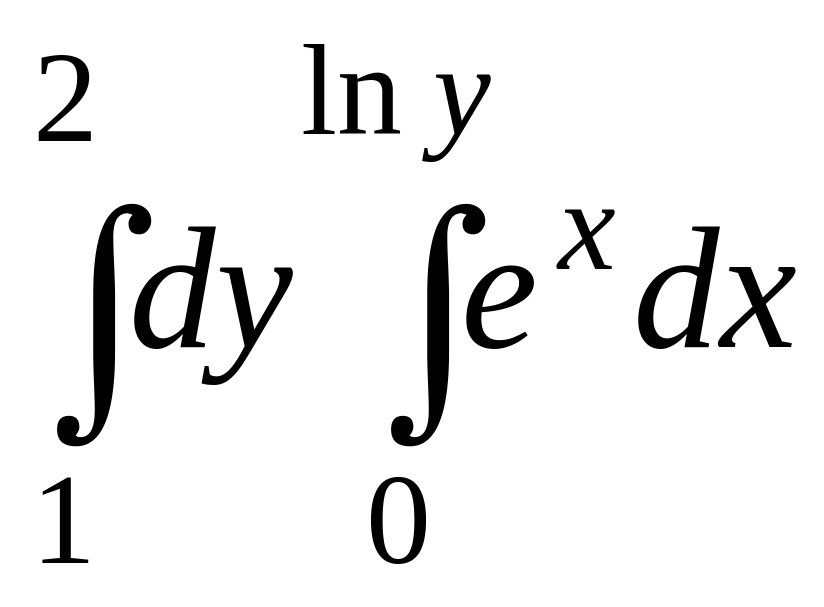
Вычислить
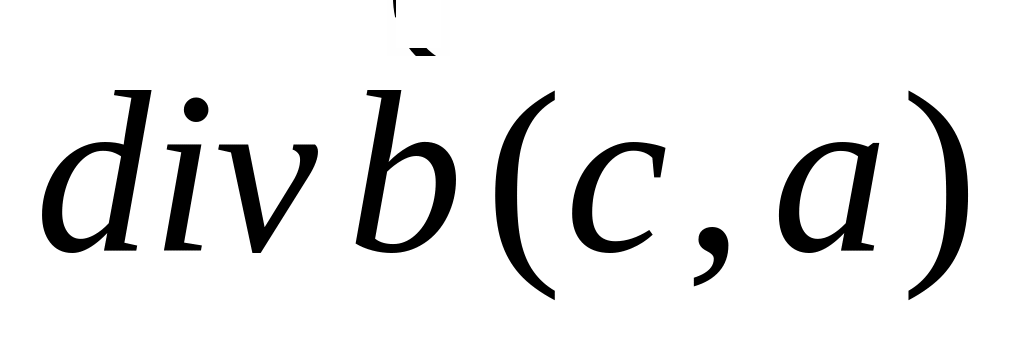 ,
если
,
если
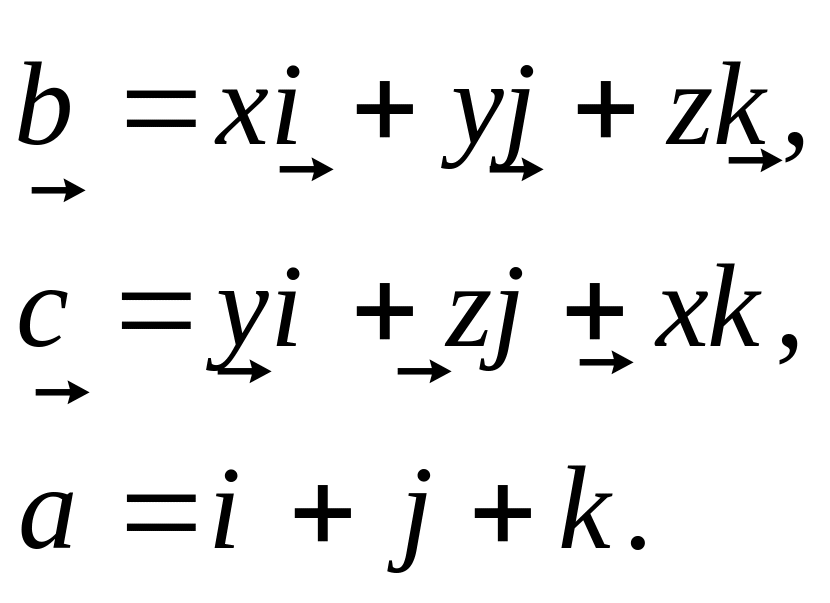
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
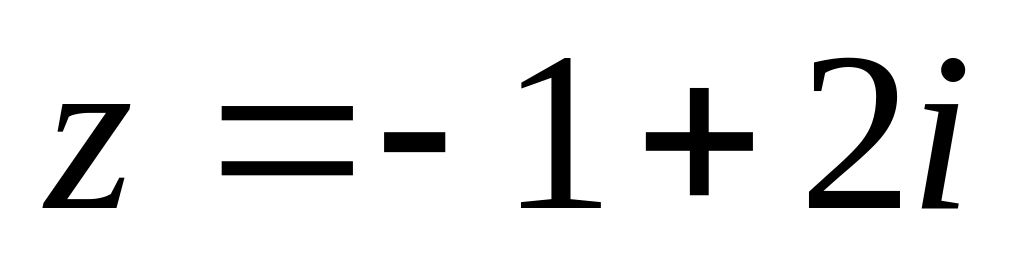 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
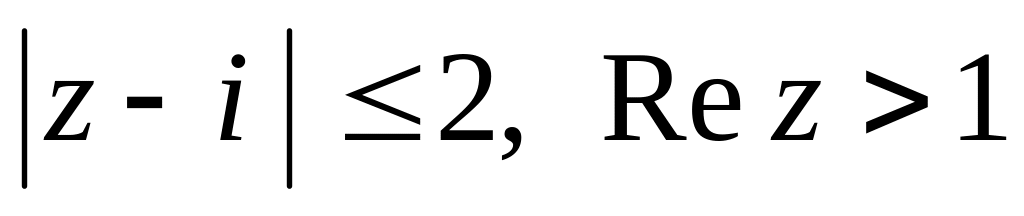 .
.
Вариант № 4
Вычислить
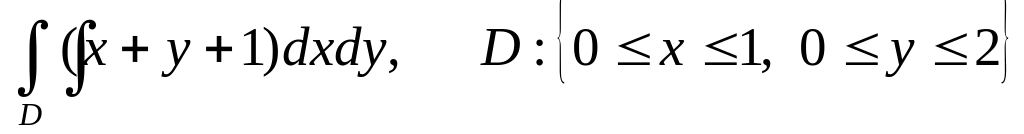

Доказать, что
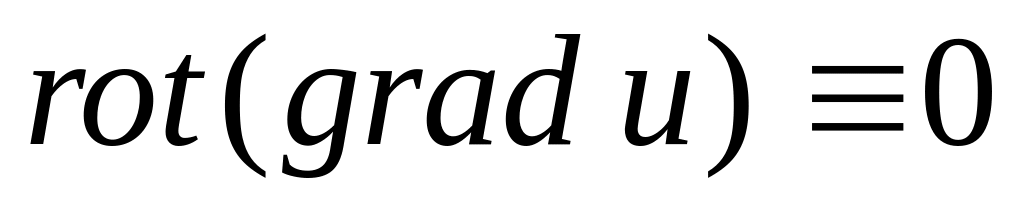 ,
,
где
![]() - произвольная функция декартовых
координат X,
y
и z.
- произвольная функция декартовых
координат X,
y
и z.
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
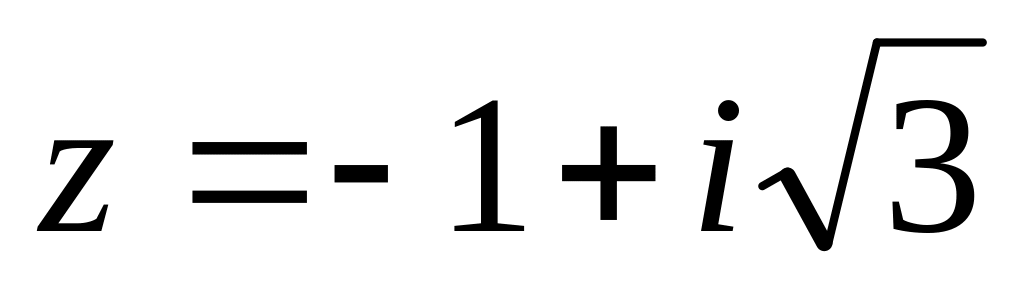 и записать его в тригонометрической
форме.
и записать его в тригонометрической
форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
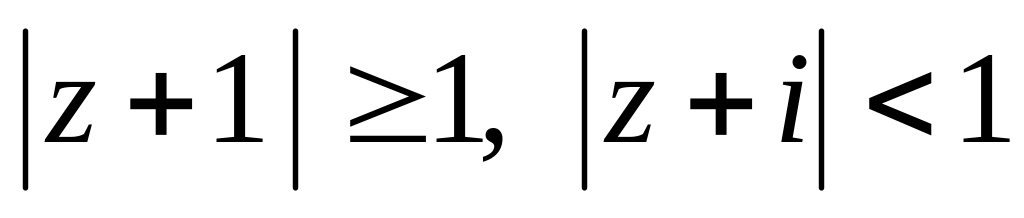 .
.
Вариант № 5
Вычислить
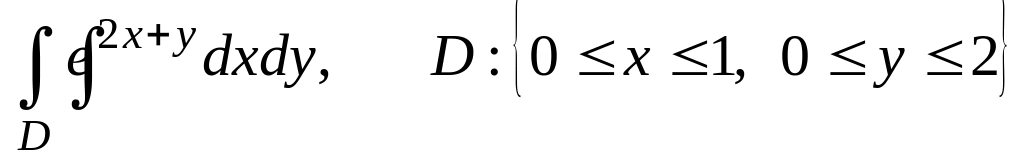
Вычислить
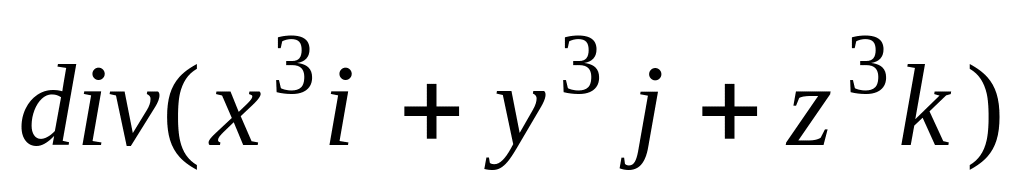
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
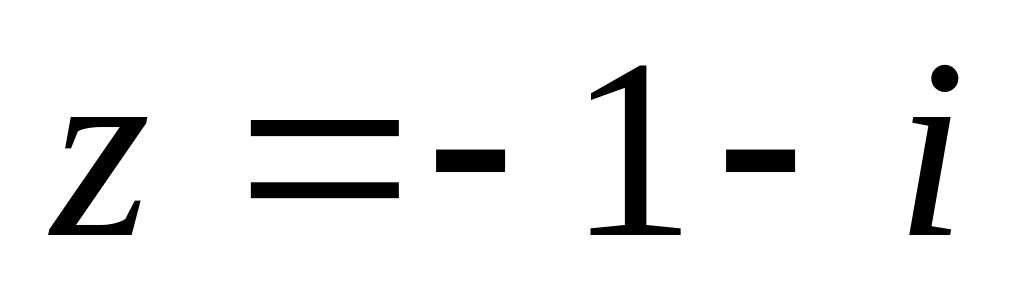 и записать его в тригонометрической
форме.
и записать его в тригонометрической
форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
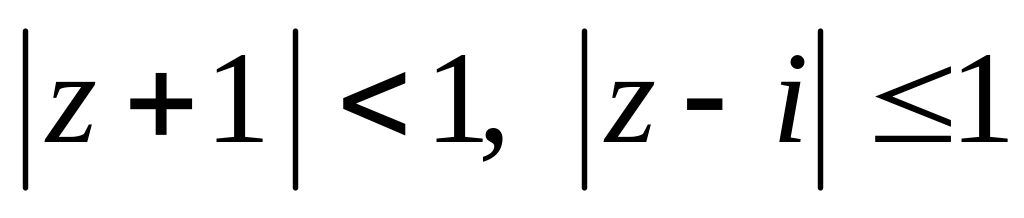 .
.
Вариант № 6
Вычислить
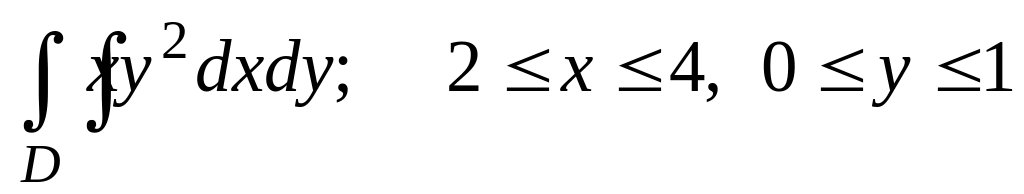
Вычислить
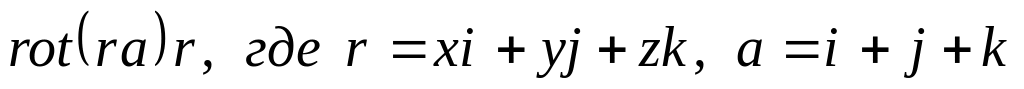
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
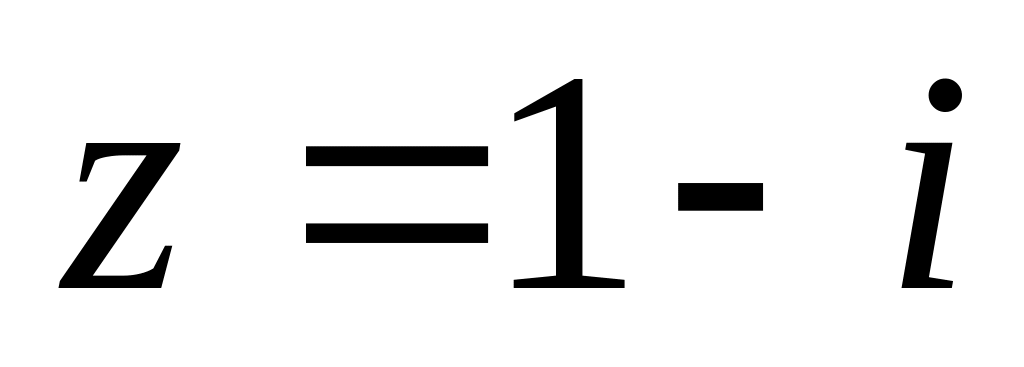 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
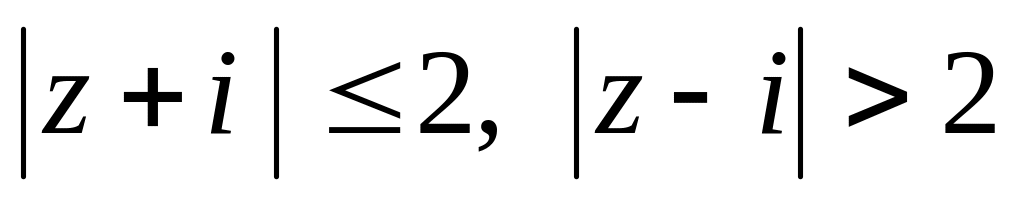 .
.
Вариант № 7
Вычислить
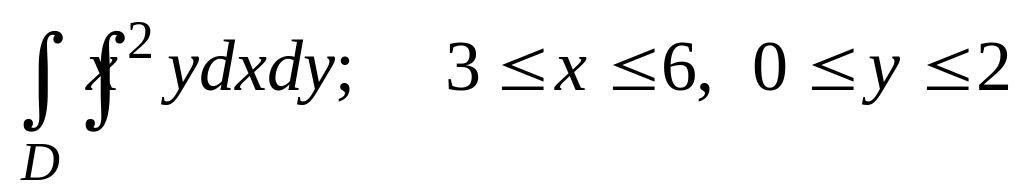
Вычислить
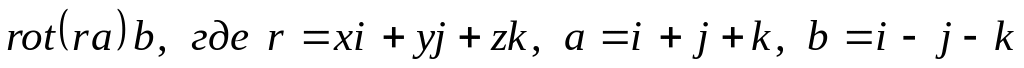
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
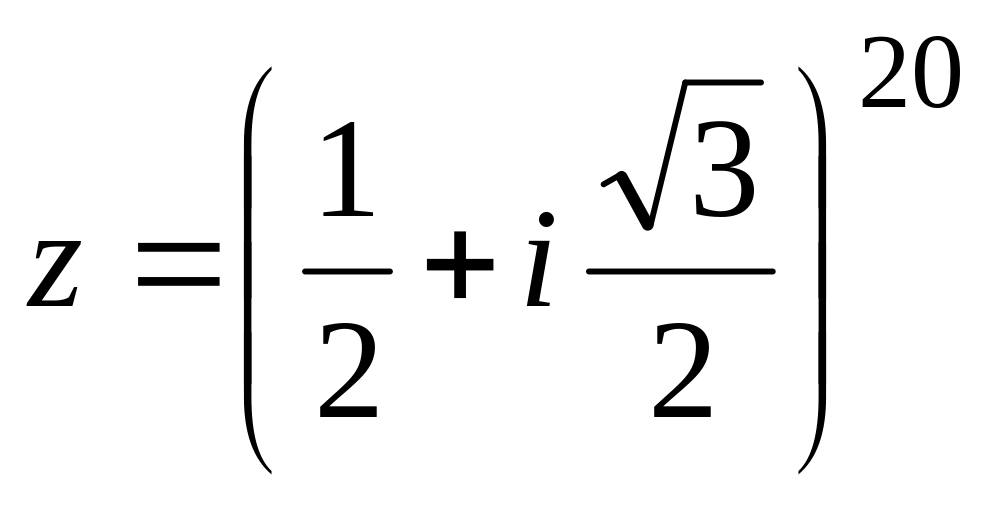 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
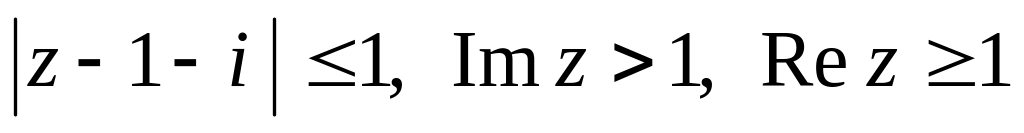 .
.
Вариант № 8
Вычислить
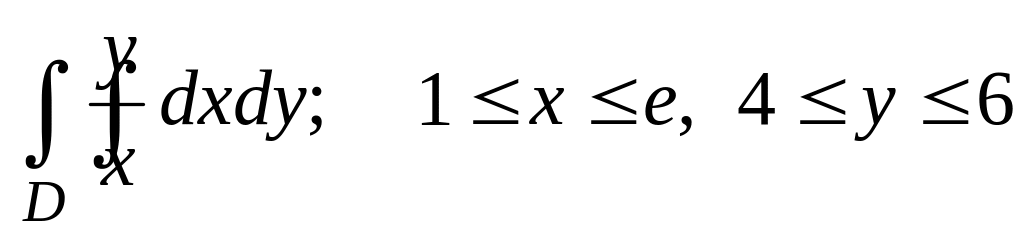
Вычислить
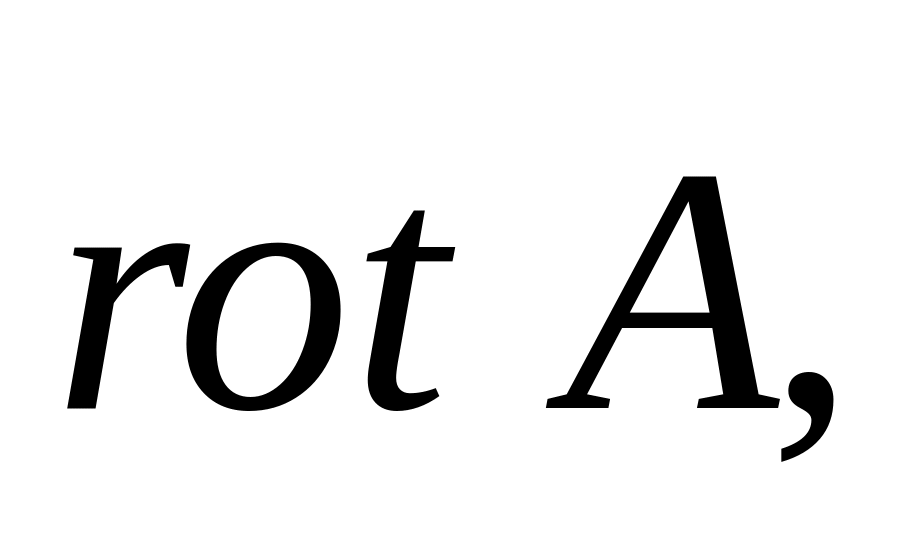 если
если
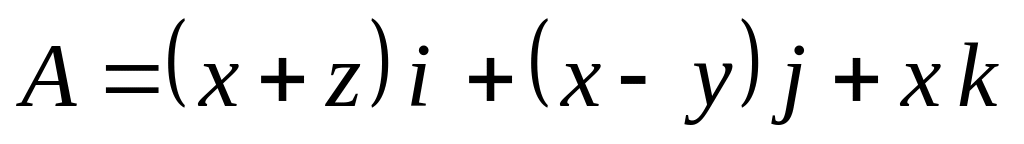
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
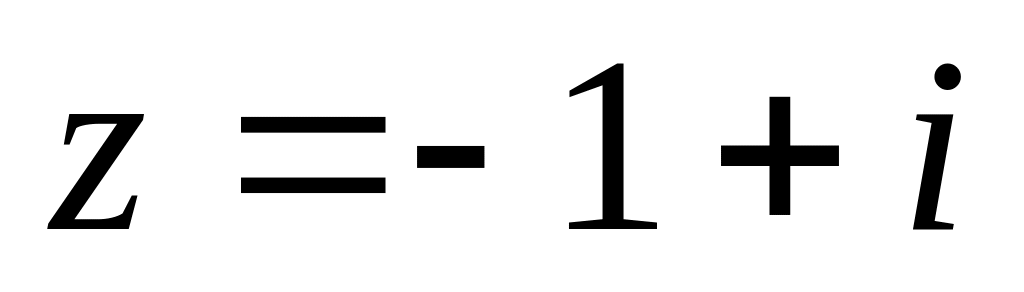 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
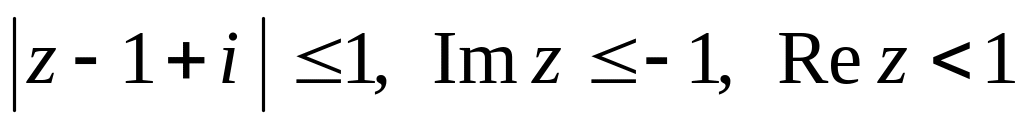 .
.
Вариант № 9
Вычислить
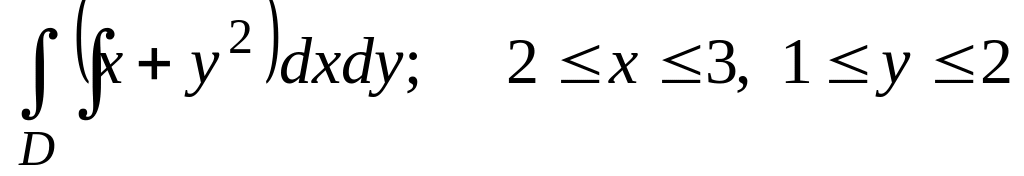
Вычислить
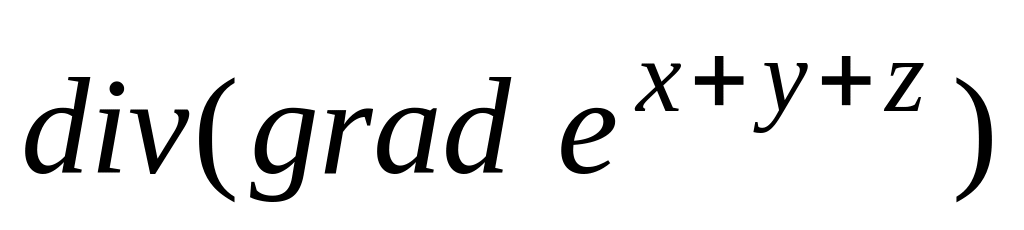
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
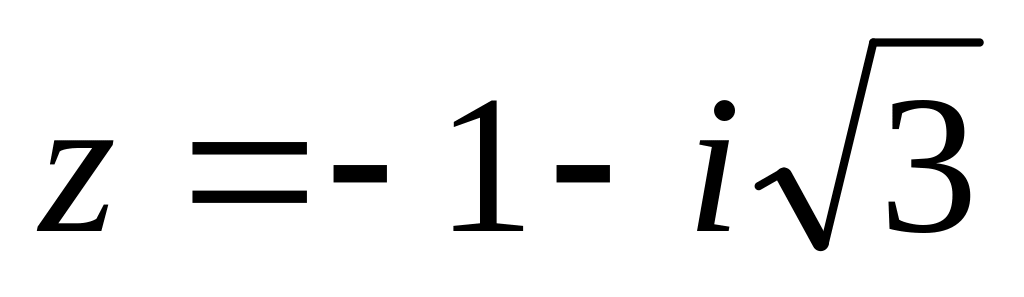 и записать его в показательной форме.
и записать его в показательной форме.Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
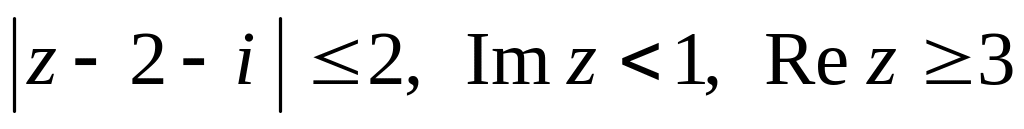 .
.
Вариант № 10
Вычислить
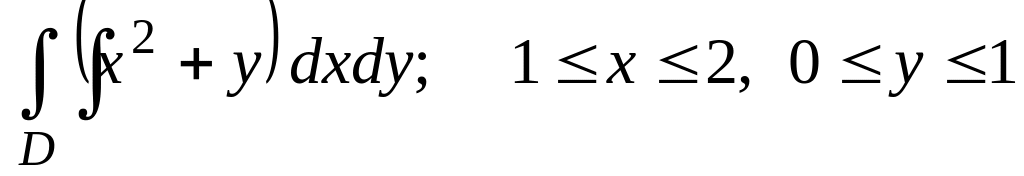
Вычислить
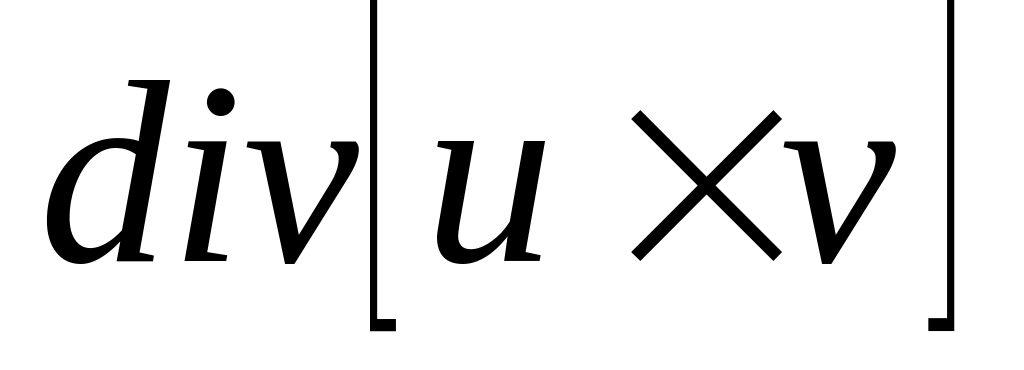 ,
где
,
где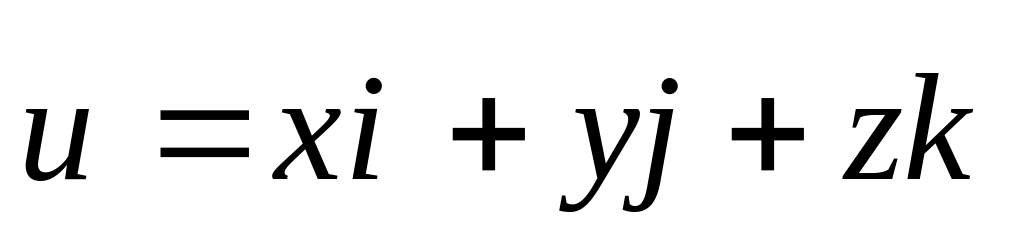 ,
,
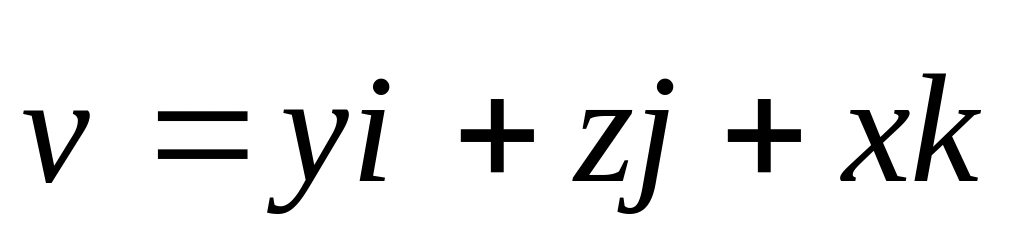
Найти модуль и множество значений аргумента (выделив его главное значение) комплексного числа
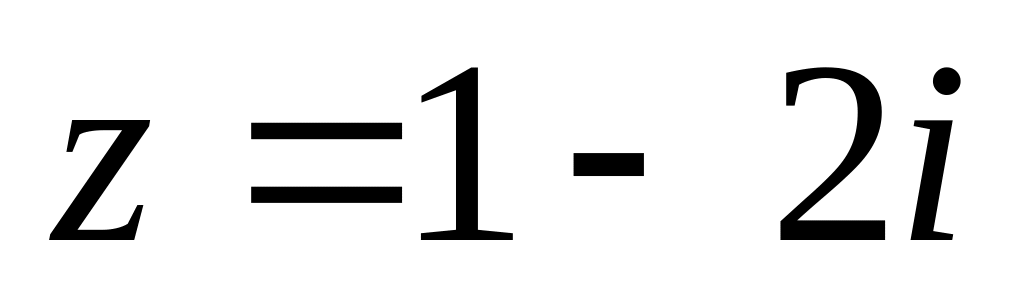 и записать его в показательной форме.
и записать его в показательной форме.
Изобразить на комплексной плоскости область, удовлетворяющую неравенствам
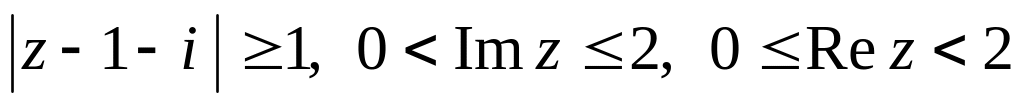 .
.
