10

Лабораторная работа № 1 Тема: «Исследование основных логических элементов» Цели лабораторной работы:

• Учебные

• формирование практических умений по изучаемой теме;

• применение изученного материала для выполнения последующих лабораторных работ по изучению принципа работы комбинационных узлов, собранных на основных (базовых) логических элементах;

• Развивающие

• расширение кругозора студентов по изучаемому вопросу;

• умение работать со средней сложности аппаратурой (стендом универсальным по основам автоматики и вычислительной техники), а также определять по таблицам истинности основные логические элементы: И, ИЛИ, И-НЕ, ИЛИ-НЕ, ИСКЛЮЧАЮЩЕЕ ИЛИ, НЕРАВНОЗНАЧНОСТЬ;

• Воспитательные

• формирование учебных и профессиональных практических умений и соз­нательного отношения к процессу обучения;

• воспитание аккуратности при выполнении работы.

Контрольные вопросы для допуска к выполнению лабораторной работы

1. Высказывание – что это?

2. Что называют логическими переменными?

3. Что называют логическими функциями этих переменных?

4. Дать определение логического элемента.

5. Какие высказывания называют эквивалентными?

6. Что называют инвертором?

7. Что называют дизъюнктором или собирательной (разделительной) схемой?

8. Что называют конъюнктором или схемой совпадений?

9. УГО, таблица истинности и определение функции логического отрицания (инверсии, операции НЕ).

10. УГО, таблица истинности и определение функции логического сложения (дизъюнкции, операции ИЛИ).

11. УГО, таблица истинности и определение функции логического умножения (конъюнкции, операции И).

12. УГО, таблица истинности и определение функции отрицания конъюнкции (элемента Шеффера, несовместимости, операции И-НЕ).

13. УГО, таблица истинности и определение функции отрицания дизъюнкции (элемента Пирса, операции ИЛИ-НЕ).

14. УГО, таблица истинности и определение функции равнозначности (эквивалентности).

15. УГО, таблица истинности и определение функции неравнозначности (сложения по модулю 2, нечётности, неэквивалентности).

Основные теоретические положения

Логические элементы – это электронные приборы, выполняющие простейшие логические операции. В настоящие время промышленность выпускает такие элементы в основном в интегральном исполнении. Логические элементы используются в большинстве цифровых интегральных микросхем, являясь их основными элементарными кирпичиками, которые во многом определяют их параметры.

Анализ работы логических интегральных микросхем базируется на использовании аппарата математической логики. Все переменные в алгебре логики принимают только два значения, «единица» или «ноль», и любые математические действия над этими переменными обеспечивают результат так же либо в виде «1», либо «0». Логические элементы дают возможность изображать логические переменные с помощью электрических сигналов (напряжения или тока). Используются два возможных способа представления логической переменной: потенциальный и импульсный. При потенциальном способе «1» и «0» соответствуют два различных уровня напряжения; при импульсном – значениям «1» и «0» соответствует появление и не появление импульсов определенные промежутки времени. Наибольшее распространение получил потенциальный способ. При потенциальном способе задания различают положительную и отрицательную логику. При положительной логике высокий уровень напряжения соответствует «1», низкий – «0»; при отрицательной логике наоборот.

Решение любой логической задачи может быть выполнено с помощью трех основных логических операций: отрицания («НЕ»), сложения («ИЛИ») и умножения («И»).

Операция «НЕ» или логическая операция отрицания означает, что при этой операции логическая функция Y противоположна аргументу X.

Аналитически это может быть записано как Y= (читается «не X»). Таблицы истинности (таблица состояния входных и выходных переменных) имеет вид:

X	Y
0	1
1	0

Логический элемент, выполняющий операцию отрицания, называется элементом «НЕ» (инвертором), условное обозначение приведено на рис. 1а.

а) б) в) г) д)

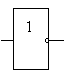
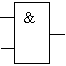
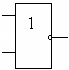
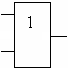
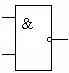
Рис. 1. Условные обозначения логических элементов:

Элемента «НЕ» (а); элемента «ИЛИ» (б); элемента «И» (в); элемента «ИЛИ-НЕ» (г); элемента «И-НЕ» (д)

Операция «ИЛИ» (логическое сложение или дизъюнкция) обозначается символами «+» или , аналитически записывается как

Y=X1+X2+…+Xn

или

Y=X1 X2 … Xn.

Таблица истинности при двух аргументах имеет вид

X1	X2	Y
0	1	0
1	0	1
0	1	1
1	1	1

Логический элемент, осуществляющий операцию дизъюнкции, называется элементом «ИЛИ», реализуется логической интегральной микросхемой, имеющей два и более входов и один выход, который принимают значения «1» всякий раз, когда хотя бы один равен «1». Условное значение приведено на рис. 1б.

Операция «И» (логическое умножение или конъюнкция) обозначается символами « » или , аналитически записывается как

Y=X1 X2 … Xn

или

Y=X1 X2 …Xn.

Таблица истинности (при двух аргументах) следующая:

X1	X2	Y
0	0	0
1	0	0
0	1	0
1	1	1

Элемент, осуществляющий операцию конъюнкции, называется элементом «И», реализуется логической интегральной микросхемой с двумя и более входами и выходом, на котором появляется сигнал «1» только тогда, когда на все входы одновременно поданы «1». Условное обозначение элемента «И» приведено на рис.1, в.

Помимо рассмотренных логических элементов широко используются универсальные, которые осуществляют две и более логических операций одновременно. Чаще всего применяются логические элементы «ИЛИ-НЕ» (элементы Пирса) и «И-НЕ» (элементы Шеффера). Уравнение функции «ИЛИ-НЕ» Y= , а функции «И-НЕ» Y= . Условные обозначения этих элементов приведены на рис.1г, д.