Закон Джоуля: внутренняя энергия идеального газа является только функцией температуры (и не зависит от объема системы).

1.3.2 Передача энергии: теплота и работа

Существует много различных способов изменения энергии систе­ мы, но с термодинамической точки зрения все они делятся на две большие группы: если энергия изменяется в результате хаотического движения частиц, принято говорить, что происходит передача тепло­ ты. Если энергия изменяется в результате согласованного и направ­ ленного движения частиц, то говорят, что совершается работа24.

При протекании химических реакций самым часто встречающим­ ся видом работы является работа расширения против сил внешнего давления. При протекании в системе электрического тока также со­ вершается работа, поскольку движение электронов - согласованное и направленное. Увеличение площади поверхности раздела фаз связано с выделением молекул из глубины фазы на поверхность, то есть с со­ вершением работы против сил внутреннего давления. В системе может совершаться работа против сил гравитационного поля, против сил магнитного поля и другие виды работ.

Будем обозначать теплоту символом Q, а работу - W.

Работа и теплота не характеризуют состояние системы; у системы не существует запаса теплоты или работы. Q и W - характеристики процесса, и говорить о них можно, только рассматривая термодинами­ ческий процесс. В зависимости от условий протекания процесса пере­ даваемая теплота и совершаемая в процессе работа могут быть раз­ личными.

Работа и теплота не являются функциями состояния.

Втермодинамике действует следующее правило знаков:

-теплота считается положительной, если она подводится к систе­ ме из окружающей среды (эндотермический процесс) и отрицательной

24 Словосочетания «передача теплоты» и «совершение работы» ис

пользуются для краткости. Точнее следовало бы говорить «передача энергии в форме теплоты» и «передача энергии в форме работы», поскольку не су­ ществует некоего объекта «теплота», который можно было бы переда­ вать от системы к системе.

34

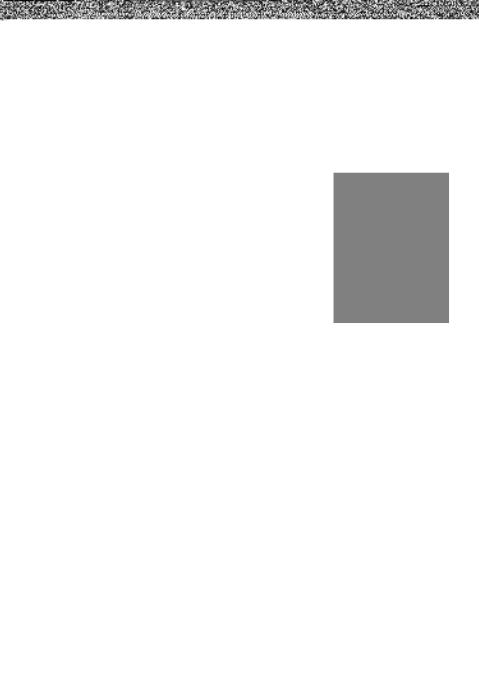
Чтобы вычислить работу, совершаемую при расширении от со­ стояния 1 (объема до состояния 2 (объема К2), необходимо проин­ тегрировать уравнение (1.8):

Результат интегрирования будет зависеть от условий протекания процесса.

1. Рассмотрим процесс, протекающий при постоянном давлении (Р = const). Константу Р в уравнении (1.9) можно вынести из-под зна­ ка интеграла:

W = p \ d v ,

у,

Если изменение температуры равно одному градусу Т2 - Т х = 1, то

W = R. Таким образом,___________________________________________

универсальная газовая постоянная численно равна работе расшире­ ния одного моля идеального газа при нагревании на один градус в изобарных условиях.

Работа расширения газа, совершающаяся в изобарных условиях, максимальна (рис. 1.19).

2. Рассмотрим процесс, протекающий при постоянной температу­ ре (Т = const).

Воспользовавшись уравнением Клапейрона-Менделеева (1.3), выразим давление через объем: Р = RT/V и подставим в (1.9):

W = RT(lnV2ln V J ,

36

нее и сложнее, чем классическая механика. Долгое время теплота и температура воспринималась как неизмеримые величины. Понятия «теплый, горячий, холодный» казались людям чем-то вроде «сладкий, горький, соленый».

Первые шаги в количественном изучении тепловых явлений мож­ но отнести к XVII веку, когда были созданы прообразы термометра - устройства О. фон Герике29 и И. Ньютона, термоскоп Г. Галилея30.

Термоскопом называется достаточно малое тело, служащее для установления одинаковости или различия температур двух тел. Термо­ скоп Галилея - это маленький стеклянный шарик, припаянный к стек­ лянной трубке. Конец трубки опускали в воду. При нагревании или охлаждении шарика давление воздуха в нем изменялось, и соответ­ ственно менялся уровень воды в трубке. При помощи такого устрой­ ства можно было судить о степени нагретости тел, но шкалы у него еще не было.

Термометр Ньютона имел 12-градусную шкалу с нулем в точке замерзания воды. Двенадцать градусов соответствовало температуре человеческого тела. Термометр Герике не показывал значения темпе­ ратуры, но давал возможность сравнивать температуру в разных по­ мещениях.

В XVIII веке были созданы термометры Д. Фаренгейта31, Дж. Делиля32, Ломоносова, Р. Реомюра33 и Цельсия, которые отличались по конструкции, но имели общую особенность: это были термометры с двумя постоянными точками, как и те, что приняты в настоящее вре­ мя. Например, в термометре Делиля в качестве рабочей жидкости ис­ пользовалась ртуть. За ноль Делиль выбрал температуру кипения во­ ды. Один градус равнялся такому изменению температуры, при кото­ ром объем ртути уменьшался на одну стотысячную. Шкала Делиля получила достаточно широкое распространение в России, ей почти сто лет пользовались многие российские ученые, в том числе Ломоносов.

С созданием термометров теплофизические опыты стали доста­ точно точными, но еще долгое время существовала большая путаница в таких понятиях, как теплота и температура, степень теплоты, коли­

29 Otto von Guericke.

30 Galileo Galilei.

31 Daniel Gabriel Fahrenheit.

32Joseph-Nicolas De VIsle.

33Rene Antoine de Reaumur.

39

Средней теплоемкостью С в интервале температур от Т\ до Т2 называют отношение

где Q - количество теплоты, подведенное к системе, АТ - вызванное этой теплотой изменение температуры.

Истинная теплоемкость С - это величина, к которой стремится значение средней теплоемкости при стремлении температурного ин­ тервала АТ к нулю.

т2- Т \1

Средняя теплоемкость в интервале температур от Тхдо Т2 числен­ но равна высоте прямоугольника, площадь которого равна площади криволинейной трапеции (рис. 1.22).

Теплоемкость вещества относят к количеству вещества. Теплоем­ кость одного килограмма вещества называют удельной, одного моля - мольной или молярной. В термодинамических расчетах, как правило, пользуются мольными величинами.

При нагревании идеального газа поступающая теплота полностью тратится на повышение кинетической энергии движения молекул. По­ скольку внутренняя энергия одного моля идеального газа равна 3/2 RT (1.6), то при повышении температуры на один градус внутренняя энер­ гия изменится на величину

41

с = 2 > , с ( >

где С, - мольная теплоемкость компонента смеси, Ns - мольная доля данного компонента (отношение числа молей данного вещества к об­ щему числу молей всех веществ в системе):

(1-21)

vi

отличающихся особой твердостью, например, алмаза.

Правило Неймана3940-Коппа^: молекулярная теплоемкость слож­ ных твердых веществ равна сумме атомных теплоемкостей входящих в вещество элементов. Эта закономерность может быть обоснована, если предположить, что каждый атом в соединении имеет ту же тепло­ емкость, что и в свободном состоянии, что не совсем верно.

Другие полуэмпирические методы расчета теплоемкости органи­ ческих соединений основываются на предположении, что определен­ ные молекулярные группы (-ОН, СН-, -СН2, -СН3 и т.д.), входящие в состав более сложных молекул, дают строго определенный вклад в общую теплоемкость (табл. 1.3).

Общий вид зависимости теплоемкости от температуры приведен на рис. 1.25.

37 Pierre Louis Dulong.

38Alexis-Therese Petit.

39Franz-Ernst Neumann.

40Hermann Franz Moritz Kopp.

44

Таблица 1.3 - Групповые вклады вмольную теплоемкость,

-сн2-

41 КревеленД.В. Свойства и химическое строение полимеров М.: Химия,

1976.

45

При приближении температуры к абсолютному нулю теплоем­ кость правильного кристалла чистого вещества также стремится к ну­

пропорционально 73, далее - по более сложной зависимости.

На рис. 1.26 приведена температурная зависимость истинной теп­ лоемкости оксида этилена.

Возрастание теплоемкости тем сильнее, чем легче осуществляют­ ся вращательные и колебательные виды движения в молекуле и чем сложнее сама молекула.

Влияние температуры на теплоемкость неодинаково в разных ин­ тервалах температур.

1. Зависимость теплоемкости от температуры в области, близкой к абсолютному нулю (от 0 до 50 К), хорошо описывается уравнением Дебая42:

42 Petrus Josephus Wilhelmus Debije.

46

кБ - постоянная Больцмана, h - постоянная Планка43, vm- предельная частота колебаний атомов кристаллической решетки, характерная для данного вещества.

2. Для твердых тел при температуре выше 50 К и до комнатных температур пригодно уравнение Эйнштейна44:

Здесь 0 включает собственную частоту колебаний молекулы v0:

тервал, наиболее важный для химической технологии) зависимость теплоемкости от температуры выражается степенными рядами вида

где я, 6, с, с', d, d - эмпирические коэффициенты, определенные из опыта и приводимые в справочнике (в расчетах с достаточной степе­ нью точности можно ограничиться коэффициентами я, Ъ, с, с').

В настоящее время уравнения типа (1.26) чаще применяют для ор­ ганических веществ, уравнения типа (1.27) - для неорганических.

Поскольку уравнения (1.26) и (1.27) - эмпирические и справедли­ вые только для определенного интервала температур, ошибкой будет рассматривать коэффициент а как теплоемкость при Т = 0 К.

Зная теплоемкость, можно по уравнению (1.16) определить коли­ чество теплоты, необходимое для нагревания некоторого количества вещества от температуры Т\ до температуры Т2. В зависимости от условий нагревания используют СРили Су.

43Max Karl Ernst Ludwig Planck.

44Albert Einstein.

47

Если температурный интервал невелик, то зависимостью тепло­ емкости от температуры можно пренебречь, тогда

где у - количество вещества (моль).

Если необходимо учесть зависимость теплоемкости от температу­ ры, то выписывают из справочника соответствующие коэффициенты зависимости С =Д7), например:

Теплоемкость жидкостей слабо зависит от температуры и этой за­ висимостью достаточно часто пренебрегают.

Теплоемкость реальных газов зависит как от температуры, так и от давления газа, причем зависимость теплоемкости от давления про­

48

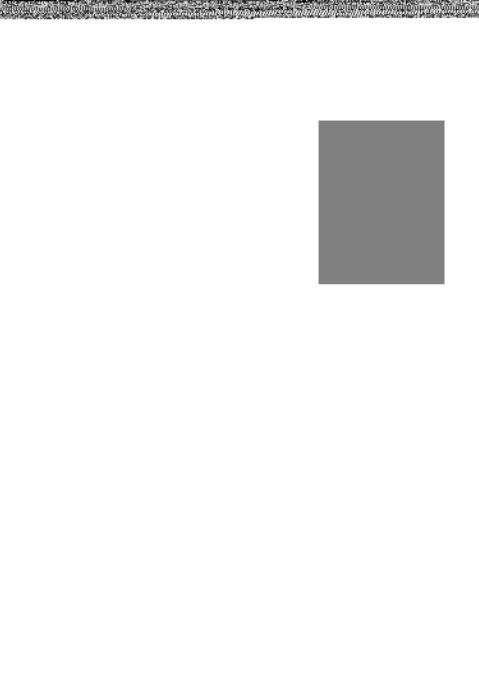
были скорее неким философским умозаключением, нежели законом физики. Перелом произошел с введением в лексикон физики понятия энергии как общей количественной меры движения и взаимодействия всех видов материи.

И наконец, в середине XIX в. различными учеными в разных странах независимо друг от друга был сформулирован Первый закон термодинамики.

Первый закон термодинамики - один из фундаментальных и аб­ солютных законов физики. Математически Первый закон никак не вы­ водится, он не может быть доказан логическим путем, он сформулиро­ ван на основе всей суммы человеческих знаний, всего накопленного нами опыта и принимается нами как аксиома. По своей сути Первый закон термодинамики - это приложение всеобщего закона сохранения и превращения энергии для термодинамической системы.

Существует несколько формулировок Первого закона:___________

- Энергия не исчезает и не возникает; она лишь переходит из од­ ного вида в другой всегда в одних и тех же количественных соотно-

4 6

шениях.46

46 Вот что пишет К.А. Путилов: «На рубеже нашего века открытие радиоактивности вызвало дискуссию о законе сохранения энергии. При этом такой крупный ученый, как Содди, настойчиво высказывал сомнение в уни­ версальности закона сохранения энергии. Вскоре, однако, было показано, что явления радиоактивности слуэ/сат к вящему торжеству принципа сохране­ ния энергии.

В 1924 г. по вине Бора, Крамерса и Слэдса снова возникла дискуссия о границах применимости закона сохранения энергии. Бор, Крамере и Слэдс выдвинули идею, что для микропроцессов, а .именно для процессов излучения и поглощения энергии, закон сохранения энергии оправдывается только как закон статистический, т. е. определяет средние величины. Для отдельных же индивидуальных актов названные ученые предполагали возмоэ/сным допу­ стить, что закон сохранения энергии вовсе не соблюдается. Эта гипотеза могла быть проверена экспериментально. А именно, если бы дело обстояло так, как указывали Бор, Крамере и Слэдс, то в явлении Комптона (в рассея­ нии рентгеновских лучей при соударении кванта рентгеновских лучей с элек­ троном) углы отлета электрона долэ/сны были бы оказаться распределен­ ными по закону случая. В 1925 г. опытами Боте и Гейгера (по изучению явле­ ния Комптона) было строго доказано, что закон сохранения энергии спра­ ведлив для индивидуального акта — столкновения кванта лучистой энергии с электроном. Дискуссия прекратилась. Однако в 1933— 1934 гг. дискуссия о законе сохранения энергии вновь возникла в связи с обсуэ/сдением причин не-

51

Последняя формулировка дает математическую форму записи Первого закона:

Если процесс протекает в равновесных и обратимых условиях, то конечное состояние системы бесконечно мало отличается от началь­ ного и тогда вместо (1.30) следует записать

Докажем на основе Первого закона, что внутренняя энергия явля­ ется функцией состояния.

Пусть в изолированной системе происходит переход из первого состояния А во второе состояние В. Представим, что этот переход мо­ жет быть совершен двумя путями. Обозначим изменение внутренней энергии при переходе по первому пути Д£/|, а по второму Д£/2. Пред­

прерывности спектра бета-лучей. Гипотеза Ферми о нейтрино положила конец этой дискуссии, и снова было утверждено торжество закона сохра­ нения энергии.

В 1936 г. дискуссия о границах применимости закона сохранения энергии возникла снова — по вине опытов американского физика Шенклэнда.

Эти опыты опять касались изучения эффекта Комптона. Он получил результаты совсем не те, которые были получены раньше в упоминавшихся опытах Боте и Гейгера. На этот раз многие из крупных ученых высказали предполоэ/сение, что закон сохранения энергии не всегда применим, а значит, не может и претендовать на роль принципа, служащего основой нашего научного мировоззрения. Конечно, это привлекло внимание экспериментато­ ров, и на протяж:ении 1937 г. в четырех крупнейших лабораториях были тщательно поставлены опыты в целях проверки результатов Шенклэнда, причем во всех четырех лабораториях было обнаруэ/сено, что Шенклэнд в своих выводах неправ. Закон сохранения энергии опять восторжествовал».

Источник: Путилов К.А. Термодинамика. М.: Наука, 1971.

47 Парижская Академия наук отказалась от рассмотрения проект вечного двигателя еще в 1775 году, задолго до открытия первого закона термодинамики.

52

положим, что изменение внутренней энергии зависит от пути процесса и AU\ > AU2. Тогда переходя из состояния А в состояние В путем 1, а затем обратно путем 2, получали бы выигрыш энергии AU\ - AU2. Но по условию система - изолированная, она не обменивается с окружа­ ющей средой ни теплом, ни работой и запас ее энергии согласно Пер­ вому началу термодинамики должен быть постоянным. Таким обра­ зом, сделанное предположение ошибочно. Изменение внутренней энергии AU не зависит от пути процесса, следовательно, внутренняя энергия является функцией состояния системы.

1.3.6Применение Первого закона термодинамики

кнекоторым системам. Энтальпия

Вобщем случае работа может быть выражена суммой

где PdV - работа расширения, W* (так называемая полезная работа) - сумма других видов работ: против гравитационных, электрических и других сил.

Если в системе совершается только работа расширения, а другие виды работ отсутствуют, то Первый закон термодинамики (1.31) мож­ но записать как

1. При изотермическом процессе Т = const, внутренняя энергия системы не изменяется dU = 0, следовательно,

SQT= dW = PdV.

(нижний индекс Т означает постоянство температуры), т.е. все тепло, подведенное к системе, расходуется на совершение работы.

2. Для изохорного процесса V = const, работа расширения не со­ вершается, PdV = 0, и уравнение 1.33 примет вид

(нижний индекс V означает постоянство объема). Или для конечного изменения

Qv = AU.

Отсюда для истинной мольной теплоемкости при постоянном объеме вместо (1.15) можно записать:

53

3.В адиабатическом процессе система не обменивается теплото

сокружающей средой:

<5£ = 0.

Следовательно,

PdV = -dU.

Работа в адиабатическом процессе совершается за счет убыли внутренней энергии. Из выражения (1.35) dU = CydT, поэтому

8W = PdV = -CydT;

W = - f c rdT,

V\

откуда, считая теплоемкость Cv постоянной величиной, можно полу­ чить формулу для вычисления работы расширения в адиабатическом процессе:

4. Для изобарного процесса Р = const\ константу можно внест под знак дифференциала, и тогда уравнение (1.33) примет вид

SQp = dU + d(PV) = d(U + PV).

Сумма U + PV используется так часто и имеет настолько большое зна­ чение, что ей дали собственное название - энтальпия Я (от греч. enthalpo - согреваю):

Поскольку энтальпия равна количеству теплоты, подведенной к системе (или отведенной от нее) в условиях постоянства давления, то ее часто называли тепловой функцией или теплосодержанием.

На практике чаще всего приходится иметь дело с изобарными условиями (протекание процесса при постоянном атмосферном давле­ нии), когда тепловой эффект процесса совпадает с изменением эн­ тальпии системы. Поэтому вместо термина «тепловой эффект реак­ ции» по умолчанию используют термин «изменение энтальпии реак­ ции».

Используя функцию Н, запишем для изобарного процесса:

54

Или для конечного изменения

QP = АН.

Отсюда для истинной мольной теплоемкости при постоянном давле­ нии вместо (1.15) можно записать:

dT

Энтальпия - это функция состояния, зависящая от температуры и давления, соответственно, для нее, как и для внутренней энергии, можно записать полный дифференциал:

dH = дН dT + дН dP.

дТ дР

Энтальпия — величина аддитивная, т. е. для сложного процесса равна сумме энтальпий его отдельных стадий.

При постоянном давлении

Различия между внутренней энергией и энтальпией существенны для газов, а для конденсированных фаз (жидкостей и твердых тел), объем которых при нагревании изменяется незначительно, этим раз­ личием можно пренебречь.

Если система является идеальным газом, то можно использовать уравнение Клапейрона-Менделеева P V = v R T , и получить другое уравнение, связывающее тепловые эффекты при постоянном давлении и постоянном объеме:

где A v - изменение числа молей газообразных веществ в результате физического процесса или химической реакции.

Таким образом - если процесс протекает в конденсированном состоянии, то

A H = A U \

- если в ходе реакции число молей газов не меняется, A v= 0, то

АН = AU;

-если реакция гетерогенная, Дv учитывается только для газооб­ разных участников реакции.

55