
- •Методические указания к выполнению самостоятельной работы
- •230401 Информационные системы (по отраслям)
- •Пояснительная записка
- •Содержание
- •VII. Список рекомендуемой литературы, Интернет-ресурсов........................16
- •I. Виды самостоятельной работы и их распределение по учебным темам дисциплины " Элементы высшей математики "
- •Тема 1. Элементы линейной алгебры
- •Тема 2. Элементы аналитической геометрии
- •Тема 3. Основы математического анализа. Дифференциальное и интегральное исчисление
- •Тема 4. Дифференциальные уравнения
- •II. Методические указания к выполнению расчётно-графической работы по индивидуальным заданиям
- •Критерии оценивания расчётно-графической работы по индивидуальным заданиям
- •III. Методические указания к cоставлению индивидуального наглядного материала по темам
- •V. Методические указания к подготовке презентаций
- •Ещё несколько тонкостей
- •Этапы подготовки презентации
- •VI. Методические указания к выполнению заданий "Математического тренинга"
- •Критерии оценивания выполнения заданий "Математического тренинга"
- •VII. Список рекомендуемой литературы, Интернет-ресурсов
- •Расчётно-графическая работа
- •230401 Информационные системы (по отраслям)
- •Вариант №
- •Решение:
- •Вычисление определителей с помощью теоремы Лапласа
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •Решение:
- •« Определение характера точки разрыва графика функции и схематическое построение графика вблизи точки разрыва» Теория
- •Асимптоты графиков функций
- •Решение:
- •Задание 2. Построить график функции без применения производной
- •Решение:
- •«Исследование функции по первой и второй производной и построение графика функции»
- •Решение:
- •Решение:
- •2. Исследуем функцию на монотонность и на экстремум:
- •3. Исследуем функцию на перегиб:
- •«Дифференциал функции и его применение в приближенных вычислениях» Теория:
- •Решение:
- •Решение:
- •Опорный конспект по теме «Дифференциальное исчисление» Контрольные вопросы
- •Опорный конспект по теме «Интегральное исчисление» Контрольные вопросы
- •Опорный конспект по теме «Дифференциальные уравнения» Контрольные вопросы
- •Математический тренинг
- •Тема 1. Элементы линейной алгебры
- •Тема 2. Элементы аналитической геометрии
- •Тема 3. Основы математического анализа. Дифференциальное и интегральное исчисление
- •Тема 4. Дифференциальные уравнения
« Определение характера точки разрыва графика функции и схематическое построение графика вблизи точки разрыва» Теория
Непрерывность функции в точке и на отрезке.
Точки разрыва графика функции и их характер.
Свойства непрерывной на отрезке функции.
Асимптота графика функции.
Определение.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() ,
если в этой точке выполнены три условия:
,
если в этой точке выполнены три условия:
1. Существуют левосторонний и правосторонний пределы функции;
2. Существует сама функция в этой точке;
3.
Значение функции в этой точке равно
значениям односторонних пределов
функции в этой точке: ![]() .
.
Если будет нарушено, хотя бы одно из этих равенств, то функция не будет являться непрерывной, и сама точка х=а , будет называться точкой разрыва.
Определение.
Точкой разрыва первого рода называется
такая точка
,
в которой существуют и равны друг другу
оба односторонних предела, но не
существует сама функция ![]() в этой точке, либо она существует, но не
равна односторонним пределам
в этой точке, либо она существует, но не
равна односторонним пределам


Рис 1. х=а - точка разрыва I рода Рис 2. х=а - точка разрыва I рода
Точки разрыва первого рода ещё называют точками устранимого разрыва, или точками "скачка" (Рис. 1 и Рис.2).
Точка разрыва I рода будет точкой неустранимого разрыва, если оба односторонних предела существуют, но не равны друг другу (Рис. 3).

Рис.3 х=а – точка неустранимого разрыва I рода
Определение. Точкой разрыва II рода называется такая точка х=а, в которой не существует хотя бы один односторонний предел, или не существуют оба односторонние пределы (Рис. 4,5,6).


Рис. 4. х=а – точка разрыва II рода. Рис. 5. х=а – точка разрыва II рода.

Рис. 6. х=а – точка разрыва II рода.
В точке х=а на рис.6 оба односторонние пределы функции не существуют.
Асимптоты графиков функций
Асимптотой графика функции является такая прямая, к которой неограниченно близко приближается график этой функции. Различают асимптоты вертикальные, горизонтальные и наклонные.
Если функция y = f(x) не существует в точке х = а и ее предел в этой точке не существует, то, говорят, что прямая х = а является вертикальной асимптотой графика этой функции.
Так,
![]() в точках х = -1 и х = 1 не существует, не
существуют так же пределы ее в этих
точках, это означает, что прямые х = -1 и
х = 1 являются вертикальными
асимптотами графика
этой функции.
в точках х = -1 и х = 1 не существует, не
существуют так же пределы ее в этих
точках, это означает, что прямые х = -1 и
х = 1 являются вертикальными
асимптотами графика
этой функции.
Аналогичный
пример:
![]() в точках х = -2 и х = 3 эта функция не
существует, не существуют так же пределы
ее в этих точках, это означает, что прямые
х = -2 и х = 3 являются вертикальными
асимптотами
графика этой функции.
в точках х = -2 и х = 3 эта функция не
существует, не существуют так же пределы
ее в этих точках, это означает, что прямые
х = -2 и х = 3 являются вертикальными
асимптотами
графика этой функции.
Если
функция существует для достаточно
больших x
и
![]() ,
то прямую y
= c
называют горизонтальной
асимптотой
графика этой
функции.
,
то прямую y
= c
называют горизонтальной
асимптотой
графика этой
функции.
Например:
функция
 ,
,
так
как,
![]() .
.
На
рисунке 7 приведён график функции
![]() .
Асимптоты совпадают с осями координат.
.
Асимптоты совпадают с осями координат.
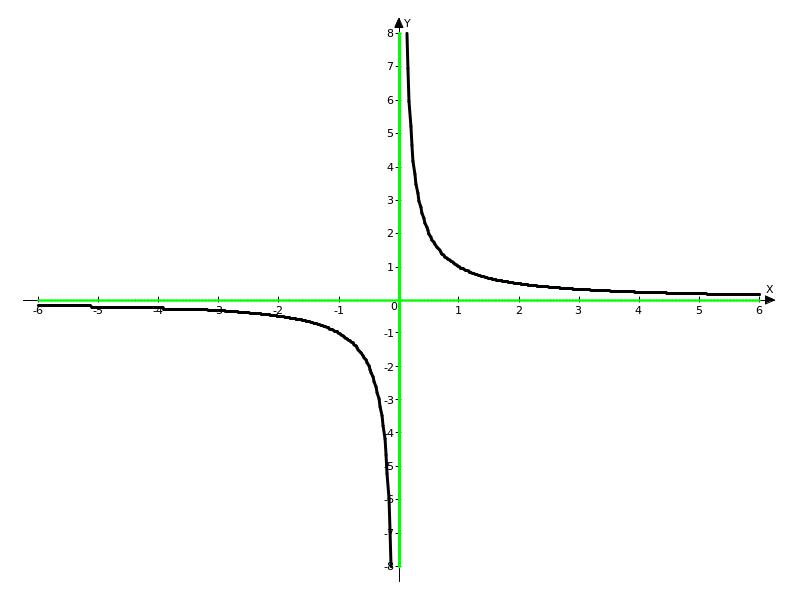
Рисунок 7. График функции
На
рисунке 8 показан график функции
![]() ,
его асимптоты: вертикальная асимптота
x
= 0 (ось Oy),
наклонная асимптота y
= x.
,
его асимптоты: вертикальная асимптота
x
= 0 (ось Oy),
наклонная асимптота y
= x.
На
рисунке 9 изображён график функции у=
![]() .
Асимптотами графика функции являются:
горизонтальная – ось ох, вертикальные
х = 1 и
.
Асимптотами графика функции являются:
горизонтальная – ось ох, вертикальные
х = 1 и
х = -1 .

Рис.8. График функции

Рис.9. График функции у =
Задание 1. Найти точки разрыва графика функции и сделать схематический рисунок графика вблизи точки разрыва.
![]() ,
, ![]()
