Решение уравнений

Excel включает большое число надстроек - откомпилированных программ, добавляющих табличному процессору новые функ­циональные возможности. Одной из таких надстроек является программа «Подбор параметра», с помощью которой можно находить в общем случае, приближенные решения уравнений вида f{x) = 0. Опишем схему использования этой надстройки на при­мере решения простого уравнения:

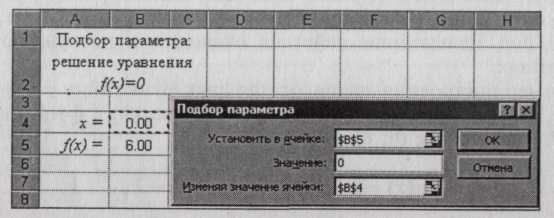
Для решения этого уравнения подготовим рабочий лист. Ячей­ка В4 будет содержать значение неизвестной х, а ячейка В5 - значение функции f(х). Для этого в В5 поместим формулу =В4*В4-5*В4+6, как показано на рис. 5.

В ыберем далее команду Сервис Подбор параметра. Excel отоб­разит диалоговое окно Подбор параметра, приведенное на рис. 6. В этом окне заполним все три окна в соответствии с результатом, который мы хотим получить. В поле Установить в ячейке введем адрес формулы (В5), результаты которой будут подобраны. В поле Значение введем желаемый результат вычисления формулы (0). На­конец, используя поле Изменяя значения ячейки, определим адрес ячейки, которая содержит значение, которое нужно изменить.

После щелчка кнопкой OK Excel выполнит необходимые вы­числения и выведет диалоговое окно Результат подбора парамет­ра (рис. 7). Ячейка В4 будет содержать найденный корень уравне­ния.

Примечание. В нашем случае уравнение имеет два корня х1 = 2 и х2 = 3. Excel всегда дает только один корень в зависимости от начального значения изменяемой ячейки.

Решение систем уравнений

Для решения систем уравнений с несколькими неизвестными надстройка «Подбор параметра» не годится, так как надо изме­нять не одну, а несколько ячеек. Воспользуемся для этой цели надстройкой «Поиск решения».

Пусть нам требуется решить систему уравнений:

Подготовим рабочий лист так, как показано на рис. 6.8. Ячейки D4 и D5 содержат формулы, выражающие левые части уравнения, ячейки Е1 и Е2 – значения неизвестных х и у (изменяемые ячейки).

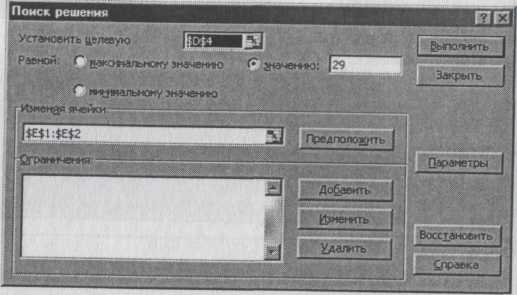
Выполним команду Сервис/Поиск решения. На экране откроется диалоговое окно Поиск решения (рис. 6.9). Установим в под Установить целевую ячейку адрес первой формулы D4, в поле Pan ной значению — число 29 (правая часть первого уравнения), а | поле Изменяя ячейки диапазон Е1:Е2.

Второе уравнение мы запишем как ограничение в поле Ограничения. Для этого нажмем кнопку Добавить и в открывшемся диалоговом окне Добавить ограничения заполним соответствующие поля как показано на рис. 6.10. После нажатия кнопки ОК про­изойдет возврат в окно Поиск решения. Нам остается только щелкнуть по кнопке Выполнить.

Результат поиска решения показан на рис. 6.11. Полученные результаты можно сохранить, нажав кнопку ОК.

Чтобы решить систему из более, чем двух уравнений, надо одно из них, например первое, выбрать как целевое, т.е. адрес соответствующей формулы внести в поле Установить целевую ячейку а остальные - как ограничения.

Надстройка «Поиск решения» как и «Выбор параметра» позво­ляет находить только одно решение системы.

В заключение добавим, что возможности надстройки «Поиск решения» не ограничиваются только решением уравнений. С её помощью можно решать довольно сложные задачи на экстремумы функций нескольких переменных при наличии о граничений на ни переменные.

*

Работа в лаборатории

Работа выполняется в Microsoft Excel

Содержание отчёта

1 . Название лабораторной работы, её порядковый номер.

2. Цель лабораторной работы.

№	Понятие, действие	Определение, последовательность команд компьютера
1	Диаграммы
2	Вставка диаграммы ……………………………..

3. Оформить ход выполнения лабораторной работы (по заданиям) по образцу:

4. Записать вывод по результатам выполнения лабораторной работы.

К онтрольные вопросы:

1. Что такое диаграммы?

2. Какие основные объекты диаграмм?

3. Перечислить основные шаги вставки диаграммы.

4. Перечислить основные типы диаграмм.

5. Для чего используется надстройка «Поиск решений»?

Литература:

1. Глушаков С.В., Ломотько Д.В. Базы данных: Учебный курс. – Харьков:Фолио, 2000, стр. 35-49