
- •Оглавление
- •Предисловие
- •Глава 1. Основные понятия термодинамики
- •1.1. Основные понятия
- •1.2. Функции перехода (процесса) и функции состояния термодинамических систем
- •1.3. Термодинамические процессы
- •1.4. Тепловые эффекты
- •1.5. Определения химической термодинамики
- •Глава 2. Постулат о существовании температуры (нулевой закон термодинамики), уравнения состояния газов
- •2.1. Нулевой закон термодинамики
- •2.1.1. Уравнения состояния газов
- •Глава 3. Первый закон термодинамики
- •3.1. Формулировки и уравнения первого закона термодинамики
- •3.2.2. Зависимость теплоемкости от температуры
- •3.2.3. Политропные процессы
- •3.2.5. Соотношение между термодинамическими параметрами, расчет теплоты, внутренней энергии и работы в политропном процессе
- •3.3. Частные случаи политропных процессов
- •3.4. Термохимия. Тепловой эффект процесса. Закон Гесса
- •3.5. Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры
- •Глава 4. Второй закон термодинамики
- •4.1. Энтропия и методы ее расчета в различных процессах
- •4.1.1. Расчет изменения энтропии в процессах нагревания или охлаждения
- •4.1.2. Расчет энтропии при фазовых переходах
- •4.1.3. Изменение энтропии идеального газа. Диффузия газов
- •4.1.4. Расчет энтропии химических реакций
- •4.1.5. Расчет энтропии химических реакций, используя электрохимические данные
- •4.2. Абсолютное значение энтропии (третий закон термодинамики)
- •5.1.Термодинамические потенциалы
- •5.2. Характеристические функции. Соотношения Максвелла
- •5.3. Изменение энергии Гиббса и энергии Гельмгольца в разных процессах
- •5.4. Изменение энергии Гиббса химической реакции по значениям стандартных энтальпий и энтропий
- •6.1.1. Задачи для самостоятельного решения (уравнения состояния газов)
- •6.2. Первый закон термодинамики
- •6.2.1. Теплоемкость
- •6.2.2. Расчет внутренней энергии, энтальпии, работы расширения, теплоты процесса
- •6.2.4. Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры
- •6.3. Второй закон термодинамики
- •6.4. Термодинамические потенциалы и основные дифференциальные уравнения химической термодинамики
- •Глава 7. Индивидуальные задания
- •Приложения
- •Приложение 1. Основные обозначения
- •Приложение 2. Справочные данные
- •Список использованной литературы
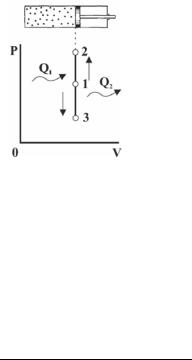
3.3. Частные случаи политропных процессов
Изохорный процесс реализуется при условии dV = 0 (V = const),
при этом работа, совершаемая газом A = 0, уравнение (3.6) примет вид
δQV = dU |
(3.73) |
QV =U2 −U1 = ∆U |
(3.74) |
т.е. количество теплоты, получаемое системой при изохорном процессе, полностью идет на увеличение внутренней энергии.
Такой процесс совершается рабочим телом (газом), находящимся в цилиндре при неподвижном поршне (рис. 3.4), если к рабочему телу подводитсятеплотаотисточникаQ1 (процесс1-2),илиотводитсятеп- лота к теплоприемнику Q2 (процесс 1-3). В координатах плоскости PV графиком изохорного процесса будет вертикаль (1-2 подвод теплоты, 1-3 при отводе
теплоты)
Интегрирование уравнения (3.58) при CV = const приводит к соотношению
QV = ∆U = nCV (T2 −T1)(3.75)
где QV – теплота, поглощенная системой при изохорном процессе; CV – молярная теплоемкость при постоянном объеме.
Уравнение изохорного процессаможетбытьполученоизтермическогоуравнениясостояния для 1 моль идеального газа (pV = nRT), если принять V = const, то в этомслучаеp/T = R/V = const илидлядвухточекизохорногопроцесса (уравнение Шарля**):
|
p1 |
|
|
|
T1 |
|
|
T p |
|
|
|
|
|
|
|
|
= |
|
|
, откуда T = |
1 |
2 |
, |
p |
|
|
|
||||||||
|
2 |
|
|
T |
|
2 |
p |
|
|
||
|
|
|
V |
|
2 |
|
V |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
подставляя это соотношение в уравнение (3.75), получим
** Ж. Шарль в 1787 г. опубликовал свои работы раньше, чем Гей-Люссак, установил зависимость объема от температуры при постоянном давлении, но он своевременно не опубликовалсвоихработ.ПоэтомуданноесоотношениетакженоситимяГей-Люссака
44
Q |
= ∆U = nC |
T1(p2 − p1 ) |
, |
(3.76) |
|
V |
V |
p1 |
|
|
|
|
|
|
|
|
|
где n – число моль вещества; p1 и p2 – начальное и конечное давление газа, соответственно.
Показатель политропы в изохорном процессе определяется уравнением (3.53) с заменой молярных теплоемкостей C на Сv
n = |
Сv −Сp |
= ±∞ |
(3.77) |
|
|||
|
Сv −Сv |
|
|
Изобарный процесс реализуется при условии dp = 0 (p = const) при этом работа, совершаемая газомδA = pdV или после интегриро-
вания
V |
V |
|
|
|
|
|
A = ∫2 |
pdV = p ∫2 dV = p(V2 −V1 ), |
|
|
(3.78) |
||
V1 |
V1 |
|
|
|
|
|
где V1, V2 – начальный и конечный объемы системы. |
|
|
||||
|
|
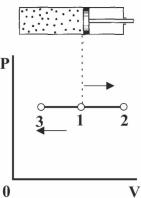
Такой процесс может проте- |
||||
|
|
кать в цилиндре, поршень кото- |
||||
|
|
рого |
перемещается |
без |
трения |
|
|
|
так, что давление в цилиндре |
||||
|
|
равно постоянному |
давлению |
|||
|
|
окружающей среды, действую- |
||||
|
|
щему на поршень с внешнейсто- |
||||
|
|
роны (рис. 3.5). В координатах |
||||
|
|
PV графиком изобарного про- |
||||
|
|
цесса будет горизонталь (1-2 при |
||||
|
|
расширении, 1-3 при сжатии). |
||||
|
|
|
Уравнение (3.78) в сочета- |
|||
|
|
нии с уравнением состояния для |
||||
|
|
1 |
моль |
идеального |
газа |
|
Рис. 3.5 Изобарный процесс в PV- |
pV = nRT |
приводит к соотно- |
||||
шению |
|
|
|
|||
координатах |
|
|
|
|
||
A = p(V2 −V1 )= nR(T2 −T1 ). |
|
|
|
(3.79) |
||
|
|
45 |
|
|
|
|
Количество тепла, поглощаемого газом при изобарном процессе, исходя из (3.7) при Cp = const, равно
Qp = nC p (T2 −T1 ), |
(3.80) |
где Qp – теплота, поглощенная системой при изобарном процессе; Cp
– молярная теплоемкость при постоянном давлении.
Уравнение изобарного процесса может быть получено из термического уравнения состояния для 1 моль идеального газа (pV = nRT), если принять p = const, то в этом случае V/T = R/p = const, или для двух точек изобарного процесса (закон Гей-Люссака):
V1 |
|
|
T1 |
|
|
T V |
|
|
|
|
|
= |
|
|
, откуда T = |
1 2 |
, |
|
|
|||||||
V |
2 |
|
T |
|
2 |
V |
|
|
|
p |
|
2 |
p |
|
1 |
|
|
подставляя последнее соотношение в уравнение (3.79), получим
Qp = nC p |
T1(V2 −V1 ). |
(3.81) |
|
V1 |
|
Для изобарного процесса уравнение (3.6), используя уравнение (3.78), можно преобразовать к виду
Qp = (U 2 −U1 )+ p(V2 −V1 )= (U 2 + pV2 )− (U1 + pV1 ), (3.82)
т.е. для данного процесса в качестве энергетической характеристики используется не внутренняя энергия, а другая функция состояния –
энтальпия Н
H = U + pV,
т.е.
Qp = H2 − H1 = ∆H . |
(3.83) |
Изменение энтальпии зависит только от начального и конечного состояния системы.
Исходя из (3.82), (3.83) и (3.74), получим
Qp = ∆H = ∆U + p∆V = QV + p∆V . |
(3.84) |
Показатель политропы в изобарном процессе определяется из уравнения (3.53) с заменой молярной теплоемкости C на Сp:
n = |
Сp − Сp |
= 0 |
(3.85) |
|
|||
|
Сp − Сv |
|
|
46
Численное значение n = 0 для изобарного процесса могло быть получено и из уравнения политропного процесса относительно pV – переменных: pVn = const.
Сомножитель Vn должен быть равен единице, что бы выполнялось условие p = const, а произвольная величина в нулевой степени равна единице.
Изотермический процесс реализуется при условии dT = 0 или T = const. Молярная теплоемкость этого процесса согласно определе-
нию С = δdTQ и равна ∞. Изотермический процесс протекает, напри-
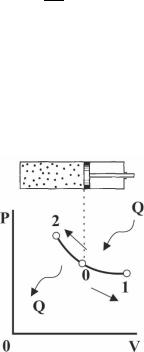
мер, в цилиндре поршневой машины, когда по мере подвода теплоты к рабочему телу поршень машины перемещается, увеличивая объем настолько, что температура остается неизменной. Уравнение изотермического процесса получается из термического уравнения состояния при T = const. В данном случае pV = RT = const. Из уравнения следует, что p2/p1 = V1/V2, т.е. при постоянной температуре давление и объем рабочего тела обратно пропорциональны (закон Бойля-Ма- риотто). В координатах плоскости pV изотерма является равнобокой
гиперболой(рис.3.6).Поскольку для идеального газа dU = CVdT, а dH = CPdT, то изотермический процесс с идеальным газом одновременно является процессом при постоянной внутренней энергии и энтальпии.
В соответствии с уравне-
нием (3.6) δQ = δA, т.е. Q = A работа 1 моль идеального газа для изотермического процесса может быть рассчитана по уравнению
Рис. 3.6 Изотермический процесс в PV-координатах
V2 |
V2 |
dV |
|
V2 |
|
|
A = ∫PdV =∫RT |
= RT ln |
|
||||
V |
|
. |
(3.86) |
|||
V |
||||||
V1 |
V1 |
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
47 |
|
|
|

Для n моль газа
Q = A = nRT ln V2 |
= nRT ln |
p1 |
. |
(3.87) |
|
|
|||||
V |
|
p |
2 |
|
|
1 |
|
|
|
|
|
Следовательно,всесообщенноегазуколичествотеплотывизотермическом процессе затрачивается на совершение внешней работы. Направление по гиперболе 0 – 1 процесс расширения (подвод теплоты),направление0– 2процесссжатия(отводтеплоты).Показатель политропы в изотермическом процессе можно записать, как
n = |
∞ −CP =1 |
(3.88) |
|
∞ −CV |
|
Аналогичное уравнение можно получить, сопоставляя термическое уравнение для 1 моль идеального газа с уравнением политропного процесса в pV переменных (pVn = const). Коэффициент распределения теплоты для изотермического процесса Ψ = dU/δQ = 0.
Адиабатный процесс расширении идеального газа реализуется
без теплообмена с внешней средой, т.е. δQ = 0, Q = 0.
Условие Q = 0 является необходимым, но недостаточным для реализации адиабатного процесса. Так, например, в начальный момент сжатиягазавцилиндредизельногодвигателятемпературастенокцилиндра выше температуры рабочего тела, в связи с чем теплота передается от стенок цилиндра рабочему телу. По мере сжатия газа его температура повышается настолько, что в конце сжатия стенки цилиндра оказываются холоднее газа, и тепловой поток меняет свое направление: теплота передается от рабочего тела стенкам цилиндра дизельного двигателя. В частном случае, количество теплоты, полученное газом от стенок цилиндра в начале сжатия, может оказаться равным количеству теплоты, отданному газом стенкам цилиндра в конце сжатия. Следовательно, суммарный теплообмен рабочего тела с внешней средой окажется равным нулю (Q = 0), хотя процесс сжатия был явно не адиабатным.
Таким образом, необходимым и достаточным условием для адиабатного процесса является условие δQ = 0.
Теплоемкостьадиабатногопроцесса С = δdTQ ,апоказательполит-
ропы
48
n = |
С −CP = |
CP = γ |
(3.89) |
|
|
С −C |
V |
C |
|
|
|
V |
|
|
Коэффициент распределения теплоты в адиабатном процессе Ψ = dU/δQ = ±∞. Уравнение адиабатного процесса относительно переменных pV имеет вид:pVγ = const и показывает, что на координатной плоскости pV адиабата расположена круче, чем изотерма, т.к. γ > 1, и является неравнобокой гиперболой. Уравнение адиабаты справедливо для условия, когда γ можно считать постоянной величиной. В действительностипоказательγявляетсяфункциейтемпературыинезначительно уменьшается с ее увеличением. При γ = f(T) уравнение адиабаты имеет сложный вид даже при линейной зависимости γ от температуры.
Изуравненияпервогозаконатермодинамики(3.6),приδQ =0следует
δA = −dU ; |
(3.90) |
A = −(U2 −U1 )= −∆U , |
(3.91) |
т.е. работа совершается системой за счет убыли ее внутренней энергии. При CV = const в соответствии с (3.75)
A = −∆U = nCV (T1 −T2 ).
Принимая во внимание уравнение адиабаты ( pV γ = const ), ра-
боту адиабатного процесса можно также вычислить по уравнениям, полученным по аналогии с уравнениями (3.67 – 3.71)
|
|
|
|
|
|
p V |
|
|
− p V |
|
|
|
|
|
|
|||||||||
A = |
|
|
1 |
|
1 |
|
|
|
2 |
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
γ −1 |
γ −1 |
|
|
|
||||||||||
|
|
|
p1V1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
A = |
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
||||||||
|
|
γ −1 1− V |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ −1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
p1V1 |
|
|
|
|
|
|
p2 |
|
γ |
|
|
(3.92) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A = |
|
|
|
|
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
|
||||
|
γ −1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1V1 |
|
|
|
|
|
p2V2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
= γ −1 |
1− |
p V |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
R |
|
|
|
|
1 |
|
1 |
|
|
|
|
||||||
A = |
|
|
|
|
|
[T |
−T |
] |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
γ −1 |
|
1 |
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|
|
где p1, V1, T1 – давление, объем и температура в исходном состоянии; p2, V2, T2 – давление, объем и температура в конечном состоянии.
В табл. 3.1 приведены основные закономерности для частных случаев политропного процесса
Характеристики политпропных процессов |
|
|
Таблица 3.1 |
||||
|
|
|
|||||
Процесс |
Математиче- |
C |
|
n |
Ψ |
Уравнение |
|
|
ская |
трак- |
|
|
|
|
состояния |
|
товка |
про- |
|
|
|
|
|
|
цесса |
|
|
|
|
|
|
Изохорный |
dV = 0 |
|
CV |
|
±∞ |
1 |
p/T = const |
|
V = const |
|
|
|
|
|
|
Изобарный |
dp = 0 |
|
CP |
|
0 |
1/n |
V/T = const |
|
p = const |
|
|
|
|
|
|
Изотермиче- |
dT = 0 |
|
±∞ |
|
1 |
0 |
pV = const |
ский |
T = const |
|
|
|
|
|
|
Адиабатный |
δQ = 0 |
|
0 |
|
γ |
±∞ |
pVγ = const |
50
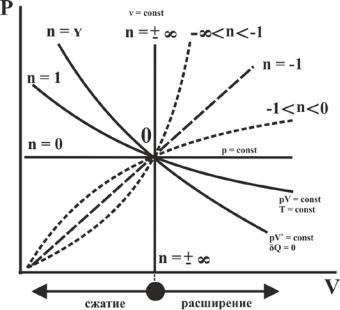
Обобщение частных случаев политропного процесса приведено на рис. 3.7. Выберем на графике политропного процесса в pV координатах некоторую точку 0 и проведем через нее рассмотренные выше кривые частных случаев политропных процессов, как в сторону расширения газа, так и в сторону его сжатия.
Рис. 3.7 Политропный процесс в PV-координатах
Из графика видно, что чем больше численное значение n, тем соответствующий политропный процесс будет описываться более крутой неравнобокой гиперболой, которая при n = оо (изохорный процесс) превращается в вертикальную линию в pV координатах.
Если проследить характер политропных процессов с произвольным значением γ, начав анализ с изобарного процесса, для которого n = 0, то можно обнаружить закономерность увеличения n при движении по часовой стрелке (рис. 3.7). При подходе к изохорному процессу показатель политропы n = ±∞ сразу же после перехода через вертикальную линию проявляются «свойства бесконечности» - знак изменяется на противоположный и в области сжатия сначала наблюдается область с отрицательными значениями n до тех пор, пока не
51
будетдостигнутизобарныйпроцесс(n =0, горизонтальная линия).В области отрицательных хначений n можно отобразить процесс с n = -1, равнозначный прямолинейному процессу, так как pV-1= p/V = const. Для этой области можно сделать вывод о том, что политропные процессы, лежащие в интервале n от - ∞ до -1, имеют выпуклостьрассматриваемыхфункцийвниз,апроцессы,лежащиевинтервале n от -1 до 0, - вверх.
Таким образом, зная показатель политропного процесса, можно оценить область, где он будет располагаться в pV координатах.
Таким образом, линии частных случаев политропных процессов разделяют все возможные процессы, проходящие через одну и ту же начальную точку, по некоторым характерным признакам:
-изохора (n = ±∞). Область, расположенная правее изохоры, характеризуется процессами расширения газа, левее – сжатия;
-изобара (n = 0). Область всех политропных процессов, расположенная ниже изобары, характеризуется процессами уменьшения давления, а выше изобары – увеличения давления;
-изотерма (n = 1). Область политропных процессов, расположенная выше изотермы, характеризуется увеличением внутренней энергии, ниже ее – уменьшением внутренней энергии;
-адиабата (n = γ). Область процессов, расположенная правее адиабаты, характеризует процессы, протекающие с подводом теплоты, а левее ее – с отводом теплоты.
Иначе:
1.В интервале 0 < n <1 политропные процессы расположены между изобарой и изотермой и протекание их можно определить следующими характеристиками:
а) расширение газа; все процессы на этом участке проходят с повышением температурыи, следовательно, с увеличением внутренней энергии газа; газ производит работу.
б) сжатие газа; на сжатие газа затрачивается работа; температура газа понижается, и внутренняя энергия его уменьшается.
2.Винтервале1<n<γполитропныепроцессырасполагаютсямежду изотермой и адиабатой:
а) расширение газа; работа газа совершается частично за счет теплоты, подведенной извне, частично за счет внутренней энергии газа.
б) сжатие газа; в процессе сжатия частично увеличивается внутренняя энергия газа, и теплота должна частично отводиться в окружающую среду.
52
3. γ < n < ∞. Эти процессы расположены между адиабатой и изохорой.
а) расширение газа; работа газа все время уменьшается, приближаясь к 0; отводимая теплота возрастает вследствие убыли внутренней энергии, и поэтому температура газа понижается быстрее;
б) сжатие газа; несмотря на то, что работа сжатия газа уменьшается, температура его увеличивается по мере приближения значений n к ∞, т.к. теплота, подводимая извне, все увеличивается; увеличение внутренней энергии газа происходит за счет суммарной теплоты, подводимой извне, и эквивалентной работы сжатия.
Кроме деления по значению показателя политропы, есть ещё ряд удобных правил.
Так как изотермы по мере удаления от начала координат характеризуют все более высокие температуры, то все процессы, идущие от начальной точки вверх и вправо от изотермы, проходят с повышением температуры газа, т. е. с увеличением его внутренней энергии. Процессы, идущие от начальной точки вниз и влево, проходят с понижением температуры газа и, следовательно, с уменьшениемеговнутреннейэнергии.Такимобразом,изотермаявляетсяграницей процессов, проходящих с увеличением и уменьшением внутренней энергии газа.
Еслирассматриватьадиабатукакграницупроцессов,томожно убедиться, что все процессы, проходящие вверх и вправо от адиабаты, идут с подводом извне теплоты, а, идущие вниз и влево, –с отводом теплоты в окружающую среду.
Как было отмечено ранее, политропные процессы – это равновесные, обратимые процессы, которые протекают при постоянной теплоемкостиС= const.Многиереальныепроцессымогут бытьприближенно описаны уравнениями для политропных процессов. Каждый политропный термодинамический процесс имеет вполне определенный, присущий ему характер распределения энергетических составляющих, входящих в уравнение первого закона термодинамики. Исходяизтеплоемкостиполитропногопроцесса,дляреальнойсистемы, можно найти коэффициент распределения тепла Ψ в политропном процессе, можно определить теплоемкость C, теплоту Q, изменение внутренней энергии U и работу расширения (сжатия) A, тем самым оценить вклад каждой энергетической характеристики в протекание рольного процесса.
53
