Глава 2. Постулат о существовании температуры (нулевой закон термодинамики), уравнения состояния газов

2.1. Нулевой закон термодинамики

Классическая термодинамика базируется на основных принципах законах, раскрытых и сформулированных в результате обобщения человеческого опыта.

Постулат о температуре (нулевой закон термодинамики) – это одинизосновныхпринциповтермодинамики,установленныйвсередине XVIII в. шотландским ученым Джозефом Блэком, и получив-

ший также название принципа термического равновесия. Его назы-

вают нулевым законом термодинамики, т.к. он подобно первому и второму законам термодинамики, открытых ранее и определяющих существование некоторых функций состояния, устанавливает существование температуры у равновесной системы, как функцию переменных свойств системы – давления и объема и был сформулирован позже, чем сформулированы первые два начала термодинамики

В современной термодинамике закон формулируется следующим образом (Р. Фаулер, 1931 г.):

две системы, находящиеся в термическом равновесии по отдельности с третьей системой, состоят в термическом равновесии между собой.

Рассмотрим три термодинамические системы, каждая из которых характеризуется давлением pi и объёмом Vi и способна обмениваться теплотой.

Для систем 1 и 2 условие термического равновесия

Тогда, согласно нулевому закону термодинамики, системы 1 и 3 также находятся в равновесии

Для решения системы трёх уравнений необходимо заменить (p1,V1) на функцию x; (p2,V2) – на y; (p3,V3) – на z. Получим

Решение относительно z последних двух уравнений даёт

19

т.е. X(x) = Y(y), следовательно, должны существовать такие функции f1(p1,V1) и f2(p2,V2), что при термическом равновесии систем 1 и 2

Используядругуюпарууравнений,получимравенствотрёхфункций

Этодаётоснованиесчитать,чтосуществуетфункцияпеременных T(p,V) = T, обладающая таким свойством, что две любые системы, находящиеся в термическом равновесии, характеризуются одинаковыми значениями T. Указанное свойство описывает систему с точки зрения «тёплая – холодная», и его можно связать с температурной шкалой.

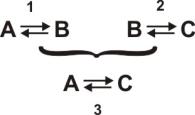
Фактически, нулевой закон вводит понятие температуры и обосновывает использование термометров – приборов для ее измерения. Предположим, что система В – стеклянный капилляр, содержащий жидкость, подобную ртути, которая сильно расширяется при нагревании. При термическом контакте системы А со второй системой В столбик ртути будет иметь определенную высоту. Если при термическом контакте системы. В с некоторой системой С высота столбика ртути останется прежней, то, в соответствии с нулевым законом термодинамики, можно предсказать отсутствие каких-либо изменений состояния систем А и С при их непосредственном контакте. Более того, положение столбика ртути целесообразно использовать в качестве температуры систем А и С.

Рис. 2.1 Схематическое описание нулевого закона термодинамики: А, С

– термодинамические системы; В – стеклянный капилляр содержащий ртуть (термометр)

20

С момента появления термометрии и по настоящее время в лабораторнойпрактикетемпературусоотносилисвысотойстолбажидкости, а разницу положений этой жидкости при контакте с тающим льдом и кипящей водой, деленную на 100, называли «градусом»: нижней точке при этом приписывали нулевое значение. Именно таким образом определяется шкала температур Цельсия. Обозначим температуру в шкале Цельсия через Tc, которая выражена в градусах Цельсия (°С). Поскольку разные жидкости расширяются в разной степени и не всегда равномерно в исследуемом интервале температур, термометры, изготовленные из разных материалов, показывают разную высоту столба жидкости для одной и той же температуры в промежутке от 0 до 100 °С. Однако, если в качестве измеряемого параметра выбрать давление газа, то можно сконструировать температурную шкалу идеального газа, которая не зависит от природы рабочего тела термометра. Шкала идеального газа полностью совпа-

дает с термодинамической шкалой температур, которая была вве-

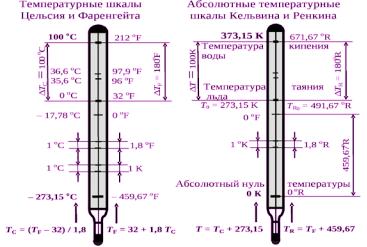
дена Кельвином (рис. 2.2) при описании работы тепловых машин, в частности работающих по циклу Карно. В качестве единственной реперной точки для термодинамической шкалы принята тройная точка воды, равная 273,15 К, а начало отсчета установлено в абсолютном нуле температур.

Рис. 2.2. Температурные шкалы и их соотношение между собой

21

В термодинамической шкале для обозначения температуры используется символ Т и температура выражается в градусах Кельвина (К). Две шкалы температур – термодинамическая и Цельсия – связаны между собой точным соотношением: Т/К = Tc/°C + 273,15.

Это соотношение можно рассматривать как рабочее определение шкалы Цельсия через более фундаментальную шкалу Кельвина.

Из нулевого закона следует, что при равновесии внутренние параметры системы являются функциями внешних параметров и температуры. Уравнение, связывающее внутренние параметры с внешними параметрами и с температурой, называется уравнением состо-

яния термодинамической системы.

2.1.1. Уравнения состояния газов

Уравнение, связывающее любой термодинамический параметр (любое термодинамическое свойство) системы с параметрами, принятыми в качестве независимых переменных, называется уравнением состояния.

В общем случае уравнение состояния имеет вид

гдеa – совокупностьвнутреннихпараметров,b – совокупностьвнешних параметров, T – температура.

Уравнение состояния может быть термическим и калорическим. Термическое уравнение состояния устанавливает связь между давлением p, температурой Т и объемом V гомогенного вещества в

состоянии равновесия f(p,T,V) = 0.

Термическое уравнение состояния

- позволяет выразить давление через объём и температуру

p = p(V,Т) и определить элементарную работу δA = pdV при бесконечно малом расширении системы dV;

-является необходимым дополнением к термодинамическим законам, которое делает возможным их применение к реальным веществам;

-не может быть выведено с помощью одних только законов термодинамики, а определяется или рассчитывается теоретически на основе представлений о строении вещества методами статистической физики.

Калорическое уравнение состояния выражает зависимость какой-

либо калорической величины (внутренней энергии, энтальпии, теп-

22

лоемкости и т.п.) от p и Т или V и Т, например, U = f (V ,T ). Суще-

ствование калорическогоуравнениясостояния следуетиз первого за-

кона термодинамики, а из второго закона термодинамики – связь между термическим и калорическим уравнениями состояния.

Если известны термическое и калорическое уравнения состояния, то с помощью законов термодинамики можно определить все термодинамические свойства системы, т.е. получить ее полное термодинамическое описание. Сами уравнения состояния нельзя вывести методами классической термодинамики, но их можно определить экспериментально.

Из уравнений состояния для различных агрегатных состояний наиболее обоснованы уравнения состояния для газов.

Простейшим термическим уравнением состояния n моль идеального газа является уравнение Менделеева – Клапейрона

где R – универсальная газовая постоянная:

R= 8,314 Дж/(моль К) = 1,987 кал/(моль К) = 0,0821 л атм/(моль К).

Уравнение состояния идеального газа Менделеева – Клапейрона

также может быть представлено следующими уравнениями:

, где m – масса газа в кг, V – объем газа в м3, Ṙ – газовая постоянная для 1 кг газа в Дж/(кг К). Газовую постоянную, отнесенную к 1 кг

газа, определяют по уравнению Ṙ = 8314 /μ (Дж/(кг К)), где μ – масса 1 кмоль газа в кг (численно равная молекулярной массе газа).

Уравнение состояния через удельный объем

, где v – удельный объем газа в м3/кг, Ṙ – газовая постоянная для 1 кг

газа в Дж/(кг К).

Для описания реальных газов, в которых частицы имеют конечные размеры и взаимодействуют друг с другом, используют более сложные уравнения состояния:

− уравнение Ван-дер-Ваальса

− уравнение Бертло

23

Уравнения (2.10) – (2.13) записаны для 1 моль газа;а - постоянная (разная для разных веществ), характеризующая взаимное притяжение молекул;b— постоянная(разная дляразныхвеществ),связанная с размерами молекул, характеризующая взаимное отталкивание молекул. Первое и второе уравнение Дитеричи являются полуэмпирическими. Они переходят в уравнение состояния идеального газа в пределе больших молярных объёмов.

Первое уравнение Дитеричи для умеренных давлений значительно лучше уравнения Ван-дер-Ваальса, но непригодно для больших давлений Коэффициенты a и b для уравнения Ван-дер-Ваальса приведены в табл. 2.1, прил. 2.

С высокой точностью поведение любого реального газа можно описать с помощью вириального разложения по степеням обратного объема

где Bi, Bi' – 1-ые вириальные коэффициенты, которые зависят от температуры.

Уравнениесостоянияидеальногогазаивириальноеуравнениесостоянияреальногогазаможновывестиметодамистатистическойтермодинамики.

Иногда уравнения состояния реальных газов записывают через приведенные переменные, которые определяют через параметры критического состояния газов

24

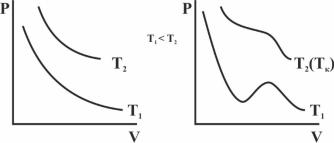
где критические параметры определяются как координаты точки перегиба на изотерме реального газа (рис. 2.3).

Рис. 2.3 Изотермы идеального газа и газа Ван-дер-Ваальса

Свойства идеальных и реальных газов отличаются из-за наличия взаимодействия между молекулами реального газа. Мерой отклонения от идеального поведения служит фактор сжимаемости

Для идеальных газов Z = 1.

Термическое уравнение состояние конденсированной фазы можно вывести в общем виде, исходя из функциональной зависимости (2.8) можно записать V = f(p, V)

Для конденсированной фазы можно принять, в первом приближе-

нии, что V = const, dV = 0

25

Уравнение (2.20) получило наименование дифференциального уравнения состояния, а входящие в него частные производные – термодинамические характеристики рабочего тела.

Входящие в это уравнение частные производные имеют физический смысл

где α – коэффициент изобарного (термического или объемного) расширения, β– коэффициент изотермической сжимаемости, γ– изохорный коэффициент давления (коэффициент термической упругости), V0 – объем при T = 0 К. Знак «минус» в выражении (2.21) вводится для того, чтобыобеспечитьположительноезначениеβ, т.к. при сжатии dV < 0.

Если известны термические коэффициенты α, β, γ, то можно получить уравнение состояния конденсированной фазы в интегральной форме. Так, если подставить выражения (2.21) в (2.20), то получим уравнение состояния конденсированной фазы в интегрально форме

Контрольные вопросы

1.Сформулируйте нулевой закон термодинамики. Выведите уравнение нулевого закона термодинамики в неявной форме. Какова математическая запись нулевого закона термодинамики и его физический смысл?

2.Какое уравнение состоянияназываетсятермическим, акакое– калорическим?

3.Запишите и охарактеризуйте уравнение Менделеева – Клапейрона.

4.Какие уравнения состояния для реальных газов Вы знаете?

26

5.Сформулируйте теорему о соответственных состояниях. Каков вид вириальных уравнений состояния?

6.Какиеметодыиспользуютсядлявыводауравненийсостояния?

7.В чем состоит значение нулевого закона в термодинамике, в физической химии?

8.Как вы понимаете – термодинамическая шкала температур?

9.Температурные шкалы и их соотношения друг с другом.

10.Объясните, почему коэффициент сжимаемости изменяется с давлением и температурой, и покажите, как с его помощью получить сведения о характере межмолекулярных взаимодействий в реальных газах.

11.В чем смысл введения критических параметров?

12.Объясните, почему коэффициент сжимаемости изменяется с давлением и температурой, и покажите, как с его помощью можно получить сведения о характере межмолекулярных взаимодействий в реальных газах.

27