Например, образование 1 моль воды при горении водорода в зависимости от ее конечного физического состояния сопровождается следующими тепловыми эффектами:
Н2 + ½ О2 = Н2О (г), ∆Н1 = –241,83 кДж; Н2 + ½ О2 = Н2О (ж), ∆Н2 = –285,84 кДж;
Н2 + ½ О2 = Н2О (т), ∆Н3 = –291,67 кДж.
Следовательно,
Н2О (т) → Н2О (ж), ∆Н4 = ∆Н2 – ∆Н3 = 5,83 кДж; Н2О (ж) → Н2О (г), ∆Н5 = ∆Н1 – ∆Н2 = 44,01 кДж;
Н2О (т) → Н2О (г), ∆Н6 = ∆Н1 – ∆Н3 = 49,84 кДж.
Закон Гесса широко применяется при различных термохимических расчетах, он дает возможность вычислить тепловые эффекты процессов, для которых отсутствуют экспериментальные данные, а во многих случаях и для таких, для которых они не могут быть измерены в нужных условиях. Это относится к химическим реакциям, процессам растворения, испарения, кристаллизации и т.д. Закон Гесса справедлив и для сложных биохимических процессов. Так, количество теплоты, получаемой при окислении углеводов и жиров в живом организме, где эти процессы протекают в несколько стадий, и количество теплоты, выделяемое при сжигании этих веществ в кислороде,оказалисьравными.Длябелковэтонетак,т.к.конечнымпродуктом окисления белка в организме является карбамид, в кислороде же окисление белка полное.
3.5. Уравнение Кирхгофа. Зависимость теплового эффекта реакции от температуры
Дифференцируя по температуре (при постоянном давлении) ра-
венство |
Н = Н2 − Н1, получаем выражение вида |
|
|
∂(ΔН)/∂T= (∂Н2/∂T)P – (∂Н1/∂T)P |
(3.100) |
где |
Н – тепловой эффект химической реакции, а индексы 1 и 2 |
|
относятся, соответственно, к продуктам реакции и исходным веществам. Здесь полезным может быть напоминание определения такой характеристики вещества, как теплоемкость. Т.е., как было рассмотрено в разд. 3.2.1, теплоемкость – количество теплоты, которое надо подать системе, чтобы увеличить ее температуру на один градус. Так как производная (∂Н/∂T)P является теплоемкостью системы при постоянном давлении, то выражение (3.100) можно переписать
∂( Н)/∂T = СP2 – СP1 = СP
или
59
∂( Н)/∂T = СP |
(3.101) |
либо с учетом определенного подведенного количества тепла к системе выражение (3.101) можем переписать
d |
[∆HT ]p= ∆Cp |
(3.101) |
|
dT |
|||
|
|
Здесь СP – изменение изобарной теплоемкости системы в химическойреакцииприпостояннойтемпературе. Дляреакции, представленной в общем виде, aA + bВ = cC + dD величина СP будет равна
СP = (c·CP(C) + d·CP(D)) − (a·CP(A) + b CP(B)),
здесь a, b, c и d – стехиометрические коэффициенты в уравнении реакции с участием веществ A, B, C и D.
Для изохорного процесса можно получить таким же путем анало-
гичное выражение |
|
||
|
d |
[∆UT ]V = ∆CV |
(3.102) |
|
dT |
||
|
|
|
|
Уравнения (3.101) и (3.102), выражающие зависимость теплового эффекта химической реакции от температуры, были выведены Кирхгофом в 1858 г. и носят название - уравнения Кирхгофа в дифференциальной форме.
Из уравнений Кирхгофа следует, что температурный коэффициент теплового эффекта процесса равен изменению теплоемкости системы, происходящему в результате процесса.
Уравнение(3.101)строгосправедливолишьприусловии,чтодавление над каждым из компонентов при искомой температуре будет таким же, как и при данной температуре. Из (3.101) следует, что чув-
ствительность ∆Н к изменению Т определяется абсолютным значением ∆СP, а знак температурного коэффициента теплового эффекта определяется знаком ∆Ср.
При ∆СP > 0 тепловой эффект реакции растет с увеличением температуры, при ∆СP < 0 уменьшается, при ∆Ср = 0 не зависит от тем-
пературы. Следует обратить внимание на то, что знак ∆Ср связан и с выбором знака тепловых эффектов.
Характер изменения ∆Н с изменением температуры обусловлен характером изменения ∆Ср с Т. Нарис.3.8 схематическиизображены всевозможныеслучаи, крометех, когда∆Н является линейнойфунк-
цией температуры. Экстремум на кривых ∆Н = f(Т) наблюдается сравнительно редко, так как обычно интервалы температур не очень
60
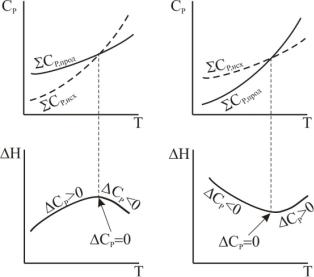
велики. Однако сама возможность появления экстремума служит указанием на недопустимость значительной экстраполяции температурной зависимости теплового эффекта за пределы опытных данных или гарантированной точности формул.
Рис. 3.8 Схема зависимостей CP и ∆H от температуры
Практически приходится чаще использовать уравнения Кирхгофа в интегральном виде. Для того, чтобы получить эти выражения, разделим переменные и проинтегрируем выражение (3.101) и (3.102). Тогда тепловые эффекты при температурах Т1 и Т2 будут связаны следующими выражениями
|
|
T2 |
|
∆HT2 |
= ∆HT1 |
+ ∫∆CP dT . |
(3.103) |
|
|
T1 |
|
|
|
T2 |
|
∆UT2 |
= ∆UT1 |
+ ∫∆CV dT . |
(3.104) |
|
|
T1 |
|
61
Прииспользованииуравнений(3.103)и(3.104) надо иметь в виду, что в температурном интервале от Т1 до Т2 не должно быть фазовых переходов веществ, участвующих в реакции.
Таким образом, зная тепловой эффект реакции при одной температуреТ1,можнонайтиегопридругойтемпературеТ2,еслиизвестны теплоемкости и их зависимость от температуры в этом температурном интервале.
При расчете ∆H можно рассматривать несколько степеней приближения:
1.при ∆Ср = 0, ∆HT2 = ∆HT1 ;
2.при ∆Ср = const, ∆HT2 = ∆HT1 + ∆C p (T2 −T1 );
3.если зависимость теплоемкости каждого вещества выража-
ется в виде степенных рядов, то для реакции ν1 A1 +ν 2 A2 =ν3 A3 +ν 4 A4 , ∆Ср выражается тоже в виде ряда
∆CP = ∆a + ∆bT + ∆c′T -2 + ∆cT 2
где
∆a = (ν3a3 +ν4a4 )−(ν1a1 +ν2a2 )= ∑νiai ;
∆b = (ν3b3 +ν4b4 )−(ν1b1 +ν2b2 )= ∑νibi ;
∆c′ = (ν3c3′ +ν4c4′ )−(ν1c1′ +ν2c2′ )= ∑νi ci′;
∆c = (ν3c3 +ν4c4 )−(ν1c1 +ν2c2 )= ∑νi ci .
Тогда
|
|
|
∆b |
2 |
2 |
|
1 |
|
|
|
′ |
||||
∆HT2 = ∆HT1 + ∆a(T2 −T1 )+ |
2 |
(T2 |
−T1 |
|
|||
)+ ∆c T |
|||||||
|
|
|
|
|
|
|
1 |
+ |
∆c (T23 |
−T13 ) |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
(3.105)
−+ T2
(3.106)
Аналогично рассчитывается изменение внутренней энергии ∆U.
Контрольные вопросы
1. Приведите несколько формулировок первого закона термодинамики и покажите, что они не противоречат друг другу. Запишите
62
математические выражения 1-го закона термодинамики в дифференциальной и интегральной формах.
2.Изменение каких величин в математических выражениях первого закона термодинамики представляет собой бесконечно-малые величины или является полным дифференциалом?
3.Перечислите способы передачи энергии от одной системы к другой. Что такое теплота и работа? Это функции состояния или функции перехода?
4.Дайте определение внутренней энергии. Каково значение ее в выражениипервогозаконатермодинамики?Перечислитееесвойства
икакие виды энергии входят и не входят в это понятие?
5.Дайте определение энтальпии. Удовлетворяет ли энтальпия свойствам функции состояния системы?
6.Запишите общее математическое выражение для работы расширения идеального газа.
7.Запишите уравнения состояния идеального газа в разных процессах: изотермическом, изохорном, изобарном, адиабатном.
8.Что такое калорическое уравнение состояние и калорические коэффициенты?
9.Дайте определение идеального газа. Что собой представляет внутренняя энергия идеального газа?
10.Почему термодинамика рассматривает не абсолютное значение внутренней энергии, а только ее изменение?
11.Что такое энтальпия и какова ее связь с внутренней энергией? Почему для конденсированных систем разница между энтальпией и внутренней энергией мала, а для систем газообразных значительна?
12.Дайте определение теплоемкости. Как связаны между собой удельная и молярная теплоемкости? Какая связь существует между молярнымитеплоемкостямиприпостоянном давленииипостоянном объеме?
13.Классификация теплоемкости по разным признакам.
14.В каких единицах измеряется теплоемкость?
15.Покажите математически переходы между различными видами теплоемкостей.
16.Приведите графическое представление средней и истинной теплоемкостей.
63
17. Запишите выражения для теплоемкости при постоянном давлении для:
-одноатомных молекул идеального газа;
-двухатомных и линейных многоатомных молекул;
-для нелинейных трехатомных и многоатомных молекул.
18.Какова взаимосвязь молярной или атомной теплоемкости для идеальных газов при постоянном объеме и при постоянном давлении (вывод уравнения Майера)?
19.Как зависит теплоемкость от температуры? Приведите примеры степенных рядов теплоемкости.
20.Дайте понятие политропного процесса. Запишите уравнение политропы относительно pV переменных. Опишите в общем виде частные случаи политропного процесса (изопроцессы).
21.Запишите основные соотношения между термодинамическими параметрами в политропном процессе (расчет теплоты, внутренней энергии и работы).
22.Дайте определение политропному процессу, приведите примеры частных случаев политропного процесса (теплота и работа изопроцессов относительно уравнения Менделеева – Клапейрона).
23.Выведите основные соотношения между термодинамическими параметрами в политропном процессе (расчет теплоты, внутренней энергии и работы).
24.Выведите уравнение политропы в pV переменных.
25.Напишите уравнения, выражающие максимальную работу расширения идеального газа при изотермическом, изобарном, изохорном и адиабатическом процессах.
26.Дайте определение обратимым и необратимым термодинамическим процессам.Приведите примеры.Можно лиреальные природные процессы считать полностью обратимыми?
27.Что называется тепловым эффектом химической реакции?
28.СформулируйтезаконГессаиследствия,вытекающиеиз него. Каковозначениеданногозакона? ПочемуQVиQpнезависятотпути протекания процесса?
29.Какая разница между понятиями: теплота в выражении для первого закона термодинамики и тепловыми эффектами Qp и QV в законе Гесса?
64
30.Объясните, почему закон Гесса есть частный случай первого закона термодинамики?
31.Применяя математическое выражение первого закона термодинамики, покажите, что тепловой эффект при постоянном давлении есть изменение энтальпии, а тепловой эффект при постоянном объеме – изменение внутренней энергии химической реакции.
32.Напишите уравнение, выражающее связь между тепловым эффектом при постоянном давлении и тепловым эффектом при постоянном объеме.
33.В каких случаях теплота – это функция процесса, а в каких – функция состояния?
34.Что понимают под стандартными условиями и стандартным состоянием?
35.Какие следствия закона Гесса Вы знаете?
36.Дайте определение понятиям: «теплота образования», «теплота разложения», «теплота растворения», «теплота сгорания», «теплота нейтрализации».
37.Какие уравнения называются термохимическими? Каким свойством они обладают?
38.Какие основные термодинамические методы для расчета тепловых эффектов химических реакций Вы знаете?
39.Почему для конденсированных систем разница междуизменением энтальпии и изменением внутренней энергии мала, а для газообразных значительна?
40.Какзависиттепловойэффектхимическойреакцииоттемпературы? Каков вид аналитической зависимости теплового эффекта реакции от температуры (уравнение Кирхгофа)?
41.Какие виды приближений используются при интегрировании уравнения Кирхгофа? В каких случаях тепловой эффект химической реакции не зависит от температуры?
65