Определенный интеграл определенный интеграл и его непосредственное вычисление

Пусть функция f(x) определена на отрезке a≤x≤b. Разобьем этот отрезок на n частей точками a<x­₀<x₁<x₂<…<x_n=b, выберем на каждом элементарном отрезке x_k-1≤x≤x_kпроизвольную точку ζ_kи обозначим через ∆x_kдлину каждого такого отрезка. Интегральной суммой для функции f(x) на отрезке a≤x≤bназывается сумма вида

Определенным интегралом от функции f(x) на отрезке a≤x≤bназывается предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

Для любой функции f(x), непрерывной на отрезке a≤x≤b, всегда существует определенный интеграл

Для вычисления определенного интеграла от функции f(x) в том случае, когда можно найти соответствующий неопределенный интеграл F(x), служит формула Ньютона – Лейбница:

Пример: вычислить следующие интегралы:

1) ; 2) ; 3)

По формуле Ньютона – Лейбница получаем:

1) ;

2) ;

3)

.

ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛОВ

1)Вычислить площадь криволинейной трапеции, ограниченной осью Оx, прямыми x = -1, у = 2 и параболой у = 9 - .

П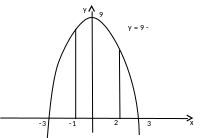 остроим график функции у = 9 - и изобразим данную трапецию

Искомая площадь S равна интегралу

.

По формуле Ньютона – Лейбница находим

Комплексные числа

Комплексными числами называют числа вида a+bi, где aи b– действительные числа, а число i, определяемое равенством , называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:

1. Два комплексных числа 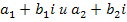называются равными, если ;

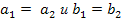2. Суммой двух комплексных чисел называется комплексное число ;

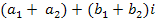3. Произведением двух комплексных чисел называется комплексное число .

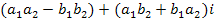ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ.

Над комплексными числами производится такие же действия, как и над действительными числами. Действия сложения и умножения даны в определении комплексного числа.

Рассматривая вычитание и деление комплексных чисел как действия, обратные соответственно сложению и умножению, получаем правила вычитания и деления комплексных чисел:

Выполнить действия: 1) (4+2i)+(1+5i); 2) (3 + 5i) – (6 + 3i).

1. По правилу сложения комплексных чисел получим

(4 + 2i) + (1 + 5i) = (4 + 1) + (2 + 5)i = 5 + 7i.

2. По правилу вычитания комплексных чисел получим

(3 + 5i) – (6 + 3i) = (3 - 6) + (5 - 3)i = - 3 + 2i.

Сложение (вычитание) комплексных чисел сводится к сложению (вычитанию) векторов, изображающих эти числа.

Дифференциальные уравнения Дифференциальные уравнения первого порядка

• Дифференциальное уравнение с разделяющимися переменными.

Х(х) У(у)dх + Х₁(х)У₁(у)dу = 0

имеет общий интеграл

Особые решения, не входящие в интеграл, определя­ются из уравнений

• Однородное дифференциальное уравнение первого порядка

Р(х, у)dх + Q{х, у)dу=0,

где Р(х, у) и Q {х, у) — однородные непрерывные функ­ции одинаковой степени, решается с помощью подста­новки

у = их

(и — новая функция).

• Линейное дифференциальное уравнение первого порядка

а(х)' + B(х)у + с(х)=0

решается с помощью подстановки у= и где и — нену­левое решение однородного уравнения а(х)у' + b(х)у =0, а новая функция.

• Уравнение Бернулли

у' + Р(х)у = Q{х)у^п (п≠0, п≠1)

с помощью подстановки z= сводится к ли­нейному делением на у^п.