
нижения температуры плавления льда I [- 0,01 (оС /атм) ]. Нетрудно сосчитать, что под давлением 10 атм вода замерзает при температуре минус 0,1 оС, под давлением 100 атм – при температуре минус 1 оС и т.д. В отличие ото льда I лед VII воды имеет совсем другие характеристики процесса плавления: р = 21680 атм, tm = + 81,6 оС. В процессе Fe (δ) → Fe (ж) молярный объем железа увеличивается. Поэтому при увеличении давления температура плавления железа растет. Возрастание ее таково: нормальная температура плавления железа tm = 1538
± 3 оС, при давлении р = 60000 атм она равна 1715 оС. Отсюда барический коэффициент повышения температуры плавления железа равен 0,003 (оС/атм), то есть влиянием давления на температуру плавления железа можно пренебрегать вплоть до давлений порядка 1000 атм.
5.5.3 Интегрирование
1) Зависимость давления насыщенного пара простых ве-
ществ от температуры. Рассмотрим равновесия т = пар и ж = пар. Двухфазные системы, отвечающие им, схематически изображены на рисунке 5.1, а, б. Оба равновесия описываются дифференциальным уравнением (5.23). Перед его интегрированием необходимо разделить переменные Т и р. Для этого в правой части этого уравнения, заменим изменение энтропии по формуле (5.16), а изменение объема вещества по формуле (5.27). Так как между молярными объемами пара и конденсированного вещества существует сильное неравенство V (пар) >> V (конд.), где конд. – сокращение термина “конденсированное вещество”, то объемом конденсированного вещества по сравнению с объемом пара пренебрежем. В результате получим:
dp |
= |
∆v H |
, |
(5.29) |
dT |
TV (пар) |
|||
dp |
= |
∆s H |
. |
(5.30) |
dT |
TV (пар) |
где ∆v H и ∆s H – изменение энтальпии при испарении и при субли-
мации 1 моль низкотемпературной фазы.
Выше (п. 3.10) найдено, что энтальпия является слабой функцией давления. Поскольку давления насыщенных паров неорганических
142
веществ, как правило, малы, то и ∆v H и ∆s H будем считать функ-
циями одной температуры. Согласно формуле (5.13) эти две величины различаются на изменение энтальпии при плавлении (∆m Н):
∆s Н = ∆v Н + ∆m Н, |
(5.31) |
причем на эту величину изменение энтальпии при сублимации превышает изменение энтальпии при испарении. Вследствие этого, при одной и той же температуре между производными от давления насыщенного пара при испарении и сублимации имеется неравенство:
|
dp |
|
dp |
. |
|
|
|
< |
|
(5.32) |
|
dT исп |
dT субл. |
|
|||
Следовательно, кривая давления насыщенного пара твердого вещества наклонена к оси абсцисс круче, чем кривая давления насыщенного пара жидкости. Иначе говоря, давление насыщенного пара над твердым веществом возрастает с температурой быстрее, чем над жидкостью. Так как формулы (5.29) и (5.30) отличаются лишь величинами, стоящими в числителях правой части, то последующие выкладки выполним для давления насыщенного пара жидкости.
Полагая насыщенный пар идеальным газом, выразим молярный объем пара через давление из уравнения Менделеева – Клапейрона (1.17): V (пар) = (RT/p). После подстановки этого значения объема формула (5.29) примет такой вид:
d ln p |
= |
∆ |
v |
H |
. |
(5.33), |
|
dT |
|
|
|||||
RT 2 |
|||||||
|
|
||||||
Она представляет собой дифференциальное уравнение Клаузиуса – Клапейрона в форме, пригодной для интегрирования. Проще всего оно производится, если изменение энтальпии при испарении считать постоянным. Обычно это предположение хорошо соблюдается в не слишком широких интервалах температуры. Произведя интегрирование, получим:
ln p =− |
∆v H |
+const , |
(5.34), |
|
RT |
||||
|
|
где в правой части второе слагаемое – постоянная интегрирования. Полученное уравнение описывает зависимость давления насыщенного пара чистой жидкости от температуры. Очевидно, что в координатах ln p, 1/Т эта зависимость является линейной, причем прямая ли-
143
ния имеет угловой коэффициент, равный: tg α = – (∆vH / R). Поскольку изменение энтальпии при испарении и универсальная газовая постоянная – величины сугубо положительные, то угол наклона прямой линии к оси абсцисс является тупым (α > 90о), то есть эта прямая линия нисходящая. Формально уравнение давления насыщенного пара твердого вещества от температуры можно получить, заменив в формуле (5.33) изменение энтальпии при испарении ∆v H на изменение
энтальпии при сублимации ∆s H. Неформально оно выводится из
формулы (5.29) посредством тех же выкладок, что и уравнение (5.33). Одно из наиболее важных применений полученного уравнения состоит в определении энтальпии испарения жидкости по опытным данным о давлении насыщенного пара. Измеренные при разных температурах давления насыщенного пара пересчитываются на ln p и (1/Т) и по этим данным по методу наименьших квадратов находится
регрессионное уравнение:
ln p =− |
(A±δA) |
+(C ±δC) , |
(5.35) |
T |
|
где A и С – константы; δA и δС – доверительные интервалы, обычно при вероятности 0,95.
Из сравнения регрессионного уравнения с термодинамическим уравнением (5.34) находим: ∆v H = R A.
Погрешность определения этой величины δ∆v H = ± R δA. Постоянная
интегрирования в уравнении (5.34) очевидно равна: const = С. К этому следует добавить, что массив опытных данных ln pi , (1/Ti ) должен
состоять не менее, чем из пяти взаимосвязанных пар, иначе погрешности определяемых величин будут слишком велики.
Уравнение (5.34) имеет и другое важное применение. С его помощью нетрудно рассчитать давление насыщенного пара при температуре Т2, если известно давление насыщенного пара при температуре Т1 и известна энтальпия испарения ∆v H. В этом случае оно имеет
следующий вид:
|
p(T |
) |
|
∆ |
v |
H |
1 |
|
1 |
|
|
|
ln |
2 |
|
= |
|
|
|
|
− |
|
. |
(5.36) |
|
p(T1) |
|
R |
|
T2 |
||||||||
|
|
|
T1 |
|
|
|||||||
Эта форма уравнения Клаузиуса – Клапейрона используется при решении таких задач, как определение изменения энтальпии при испа-
144

рении по значениям давления насыщенного пара р (Т1) и р (Т2), определение температуры кипения жидкости при заданном внешнем давлении и др.
В больших интервалах температуры (например, для твердого вещества от 0 К доTm , для жидкости от Tm доTb ) температурной зави-
симостью величин ∆v H и ∆s H пренебрегать нельзя. В этом случае
интегрирование завершается на стадии указания последующей операции:
ln p = |
1 |
∫ |
∆v H |
(T ) |
dT +const , |
(5.37) |
|
R |
T 2 |
|
|
||||
где через ∆v H (T) обозначена температурная зависимость изменения энтальпии при испарении. Так, если эта зависимость имеет вид
∆v H (T )=∆v H (Tо)+∆vCp (Tо)T , |
(5.38) |
где ∆v H ( Tо) и ∆v Cp . (Tо) – изменение энтальпии и изменение теплоемкости при испарении 1 моль жидкости при температуре Tо, то результат интегрирования будет следующим:
|
∆ |
H (Tо) |
|
∆vC p (Tо) |
|
|
||
ln p =− |
|
v |
|
+ |
|
|
lnT +const . |
(5.39) |
|
RT |
R |
||||||
Здесь в качестве температуры Tоможет быть взята любая температура с известными при ней численными значениями величин ∆v H (Tо)
и∆vCp (Tо).
2)Зависимость температуры плавления от давления. По-
скольку полиморфные превращения принципиально не отличаются от
переходов твердое вещество ↔ жидкость, то основное внимание сосредоточим на равновесии т = ж с целью определить влияние давления на температуру этого равновесия, иными словами на температуру плавления вещества. Уравнение Клаузиуса – Клапейрона (5.24) в этом случае принимает вид:
dT |
=V (ж) −V (т) T , |
|
dp |
∆mH |
(5.40) |
где V (ж) и V (т) – молярные объемы жидкости и твердого вещества; ∆m Н – энтальпия плавления 1 моль твердого вещества; T – темпера-
тура плавления твердого вещества при произвольном давлении р.
145
При интегрировании этого уравнения полагают объемы вещества в твердом и жидком состояниях и энтальпию плавления величинами постоянными, от давления независящими. Исходя из этого, получим следующую интегральную форму уравнения Клаузиуса – Клапейрона для процесса плавления:
ln |
T |
= |
V (ж) −V (т) |
(p − p |
), |
|
|
Tm |
∆mH |
(5.41) |
|||||
|
|
o |
|
где Т – температура плавления вещества при давлении р; Tm – нормальная температура плавления вещества при давлении pо(1 атм или
101325 Па).
Из приведенных выше примеров влияния давления на температуру плавления обычного льда и железа вытекает, что при малых и умеренных давлениях это влияние не велико. Этим обстоятельством можно воспользоваться следующим образом. Возьмем разность ∆m Т
= Т – Tm , представляющую по своему физическому смыслу измене-
ние температуры плавления при увеличении давления от стандартного (1 атм) до заданного р. С ее использованием левую часть уравнения (5.41) приведем к виду:
ln |
T =ln 1+ |
∆mT |
∆mT |
, |
|
|||
|
Tm |
|
|
|
|
Tm |
|
(5.42) |
|
|
Tm |
|
|
||||
|
|
|
|
|
|
|
|
|
где, разложив логарифмическую функцию в ряд Маклорена по степеням малой дроби (∆m Т / Tm ), ограничились первым членом разложе-
ния. Воспользовавшись этим результатом, получаем:
∆ T = T |
V (ж) −V (т) |
(p − p |
о |
). |
|
|
|
|
|||||
m |
m |
|
(5.43) |
|||
|
|
∆m H |
|
|
||
Согласно этому уравнению в малых и средних интервалах давления температура плавления вещества по мере увеличения давления изменяется линейно. Чтобы получить соответствующие формулы для полиморфного превращения, надо в уравнениях (5.40), (5.41) и (5.43) молярные объемы жидкости и твердого вещества заменить молярными объемами высокотемпературной и низкотемпературной модификаций, а энтальпию плавления заменить энтальпией полиморфного превращения.
146
5.6 Графики р =р (Т) и Т = Т (р)
Формулы, описывающие зависимость давления насыщенного пара от температуры и температуры плавления от давления, выводятся из уравнений (5.34) и (5.41). Произведя потенцирование этих уравнений, найдем:
|
|
− |
∆sH |
|
|
|
(5.44) |
||
p(т) =C |
e |
|
|
RT |
|
, |
|||
|
1 |
|
−∆vH |
|
|
|
|||
p(ж) =C |
e |
|
|
(5.45) |
|||||
|
|
RT |
|
, |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
V (ж)−V (т)( p−p ) |
|
|||||||
T =Tm e |
∆mH |
|
о |
(5.46) |
|||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Первыми двумя формулами описывается зависимость давления насыщенного пара твердого вещества и жидкости от температуры, третьей – зависимость температуры плавления вещества от давления. Общее свойство этих зависимостей заключается в том, что в координатах p, T и T, p все они являются экспоненциальными. При этом первые две экспоненты восходящие, тогда как третья экспонента может быть и восходящей и нисходящей. Для иллюстрации они показаны на рисунках 5.2, а, б, в на примере воды. Сплошные линии на рисунке – расчет по термодинамическим свойствам воды (таблицы 5.1 – 5.3), крестики – опытные данные. Видно, что в случае равновесия H2O (лед I) = H2O (пар) (рисунок 5.2,б) имеется хорошее совпадение расчета с опытом. В случае равновесия H2O (ж) = H2O (пар) (рисунок 5.2, а) расчетные и опытные данные близки между собой, но только в интервале температуры от – 20 оС до + 20 оС. Выше верхней границы интервала с ростом температуры расхождение между расчетом и опытом увеличивается. Причина этого заключается в постоянстве энтальпии испарения жидкой воды, принятом при выводе формулы (5.44) и использованном в расчетах равновесия H2O (ж) = H2O (пар). Из расположения на графике опытных точек относительно расчетной кривой следует, что с ростом температуры энтальпия испарения жидкой воды уменьшается. В коротких интервалах температуры зависи-
мость ∆v H о = f (T) заметного влияния на результаты расчетов
147
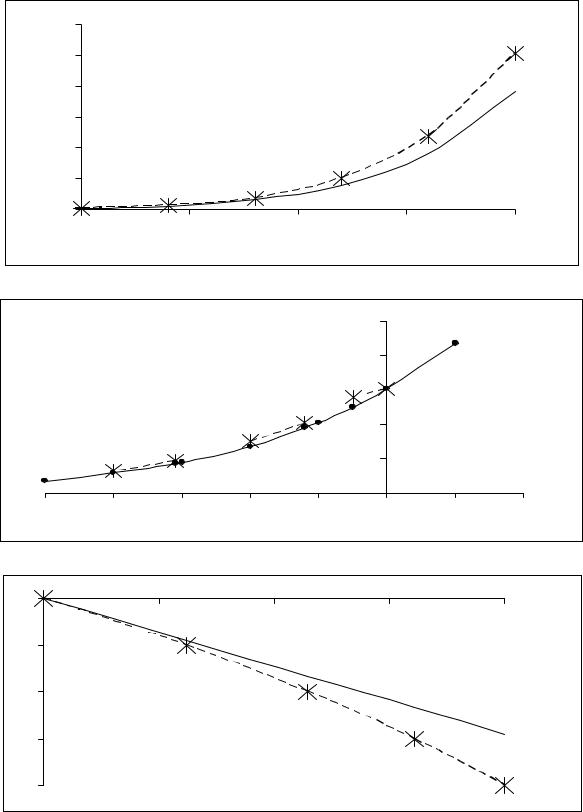
120 |
P, кПа |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
80 |
ж |
|
|
|
|
60 |
|
|
|
|
|
40 |
|
|
|
|
пар |
20 |
|
|
|
|
|
0 |
|
|
|
|
t,oC |
0 |
25 |
50 |
|
75 |
100 |
|
|
а |
|
|
|
|
|
|
1 |
P,кПа |
|
|
|
|
|
|
|
|
|
|
0,8 |
|
|
|
лед I |
|
0,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
0,2 |
пар |
|
|
|
|
|
|
|
0 |
|
t,oC |
|
|
|
|
|
|
|
|
|
|
-25 |
-20 |
-15 |
-10 |
-5 |
0 |
5 |
10 |
|
|
|
|
б |
|
|
|
|
0 |
|
|
|
|
|
|
|
P,кПа |
|
0 |
|
50000 |
100000 |
|
150000 |
|
200000 |
-5 |
|
|
|
|
|
ж |
|
|
|
|
|
|
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
-15 |
|
|
лед I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
t,oC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
Рисунок 5.2 – Зависимость давления насыщенного пара Н2О (ж) – а |
||||||||
|
|
и Н2О (лед I) - б от температуры; зависимость |
||||||
|
|
температуры плавления Н2О (лед I) от давления – в . |
||||||
148
Таблица 5.1 – Опытные и расчетные данные по давлению насыщенного пара Н2О (ж) в зависимости от температуры
|
|
|
|
|
|
|
|
|
t, 0С |
-20 |
-10 |
0 |
20 |
40 |
60 |
80 |
100 |
опыт |
|
|
|
|
|
|
|
|
Р, кПа |
0,17 |
0,30 |
0,61 |
2,34 |
7,37 |
19,9 |
47,4 |
101,3 |
расчет |
|
|
|
|
|
|
|
|
Р, кПа |
0,15 |
0,32 |
0,63 |
2,15 |
6,22 |
15,88 |
36,45 |
76,55 |
Таблица 5.2 – Опытные и расчетные данные по давлению насыщенного пара Н2О (лед I) в зависимости от температуры
|
|
|
|
|
|
|
|
|
|
|
t, 0С |
+5 |
0 |
-2,5 |
-5 |
-6 |
-10 |
-15 |
-15,5 |
-20 |
-25 |
опыт |
|
|
|
|
|
|
|
|
|
|
Р, кПа |
- |
0,61 |
0,56 |
- |
0,41 |
0,30 |
- |
0,19 |
0,13 |
- |
расчет |
|
|
|
|
|
|
|
|
|
|
Р, кПа |
0,87 |
0,61 |
0,50 |
0,41 |
0,38 |
0,27 |
0,18 |
0,17 |
0,12 |
0,07 |
Таблица 5.3 – Опытные и расчетные данные по температуре плавления Н2О (лед I) в зависимости от давления
|
|
|
|
|
|
Р, кПа t, 0С |
101,3 |
61800 |
114500 |
161100 |
2000000 |
опыт |
|
|
|
|
|
tm, 0С |
0 |
-5 |
-10 |
-15 |
-20 |
расчет |
|
|
|
|
|
tm, 0С |
0 |
-4,5 |
-8,4 |
-11,7 |
-14,5 |
не оказывает, что позволяет считать энтальпию испарения величиной постоянной. Все сказанное справедливо и по отношению к энтальпии
сублимации ∆s H о. При расчете кривой р (т) = р (Т) также было ис-
пользовано постоянное значение энтальпии сублимации. В этом случае хорошее совпадение расчетных и опытных давлений насыщенного пара объясняется узостью температурного интервала, в котором производился расчет. Несколько иначе обстоит дело с энтальпией
149
плавления. При постоянном давлении величина ∆m Ho есть функция
температуры. Эту зависимость нужно учитывать, например, в расчетах равновесий чистое твердое вещество = раствор. Однако при изучении влияния давления на равновесие т = ж температура этого равновесия (температура плавления) сама становится функцией давления. Поэтому в общем случае интегрирование уравнения (5.40) необходимо производить после подстановки в него барической функ-
ции∆m H о= F (p). На рисунке 5.2, в кривая tm = tm (p) рассчитана в
предположении независимости от давления энтальпии плавления льда I (ее постоянства; эта зависимость заметно проявляется лишь при давлениях, больших 2000 атм.). Здесь совпадение расчета с опытом скорее удовлетворительное, чем хорошее, поскольку расчетная экспонента с ее очень незначительной кривизной обращена выпуклостью вниз, тогда как экспериментальная экспонента (пунктирная линия) имеет заметную кривизну, обращенную выпуклостью вверх.
Кривыми р = р (Т) плоскость рисунка 5.2 разделяется на две области: одну, лежащую над кривой и другую, лежащую под кривой. Так как точкам кривых на рисунках 5.2, а и 5.2, б отвечают равновесные состояния двухфазных систем H2O (лед I) = H2O (пар) и H2O (ж) = H2O (пар), то естественно предположить, что и точкам областей над и под кривой также отвечают равновесные состояния, но только однофазных систем. С помощью определенных мысленных воздействий на равновесную систему “конденсированное вещество= - пар” можно легко доказать, что выше кривой р = р (Т) находится область равновесных состояний конденсированного вещества (твердого или жидкого), ниже этой кривой область равновесных состояний пара. На рисунках 5.2, а и 5.2, б области выше кривых – это области существования льда I и жидкой воды, а области ниже кривых – области существования пара.
Аналогично обстоит дело с верхней и нижней областями на рисунке 5.2, в. На этом рисунке точкам кривой tm = tm (p) отвечают равновес-
ные состояния двухфазной системы H2O (лед I) = H2O (ж). Поэтому ниже кривой располагается область однофазных состояний льда I, выше – область однофазных состояний жидкой воды. В этом нетрудно убедиться с помощью мысленных воздействий на обсуждаемую равновесную систему.
150
5.7Диаграмма состояния вблизи нормальной температуры плавления вещества
Общая особенность кривых р (т) = р (Т), р (ж) = р (Т) и Tm =
= Tm (p) в том, что все они начинаются в тройной точке, или в точке равновесия трех фаз. Вблизи температуры плавления такими фазами являются кристаллическая, жидкая и паровая. В самом деле, трехфазную систему т = ж = пар легко превратить в двухфазные равновесные системы т = ж, т = пар и ж = пар такими внешними воздействиями, как движение поршня вниз, отвод тепла от системы и подвод тепла к системе. Все эти воздействия в трехфазной системе происходят при постоянном давлении (оно равно давлению насыщенного пара) и при неизменной температуре (она равна температуре тройной точки), потому что эта система – инвариантная. Внешнее воздействие не изменяет ее параметров, но сопровождается исчезновением одной из фаз. Ясно, что исчезает та фаза, которая метастабильна (неустойчива) по отношению к данному внешнему воздействию. Поэтому попытка увеличить давление приводит к исчезновению паровой фазы и превращению трехфазной системы т = ж = пар в двухфазную систему т = ж. При отводе и подводе тепла в результате исчезновения соответственно жидкой и твердой фаз исходная система превращается в такие две системы: т = пар и ж = пар. Особенностью этих изменений в фазовом состоянии системы является то, что в момент перехода трехфазной системы в двухфазную систему параметры состояния двухфазной системы имеют те же самые численное значения, что и трехфазной. Но так как при исчезновении одной из фаз инвариантная система переходит в моновариантную, то один из параметров Т и р в этой последней системе становится функцией другого параметра. Итак, в результате превращений трехфазной системы в три двухфазные системы получаем функции р (т) = р (Т), р (ж) = р (Т) и Tm =
= Tm (p), кривые которых пересекаются на диаграмме р, Т в общей точке, названной выше тройной точкой.
Кривые этих трех функций вместе с принадлежащей каждой из них тройной точкой, построенные в координатах р, Т, образуют диаграмму, называемую диаграммой состояний вещества. В качестве примера на рисунке 5.3 приведена схематическая диаграмма состояний вещества при условиях, близких к его нормальной температуре плавления.
151
