
- •Арифметичні цикли
- •Теоретичні відомостi
- •Приклад програми
- •Варіанти завдань
- •Ітераційні цикли
- •Теоретичні відомостi
- •Цикл з передумовою
- •Цикл з постумовою
- •Приклад програми
- •Варіанти завдань
- •Складні цикли
- •Теоретичні відомостi
- •Вкладеність циклів
- •Оператор переривання break
- •Оператор продовження continue
- •Приклад програми
- •Варіанти завдань
- •Контрольні питання
Варіанти завдань
Дано натуральне число n. Отримати всі прості дільники цього числа.
У числі 222** дописати замість зірочок дві цифри так, щоб дане число ділилося на 15
Дано натуральне число n. Серед чисел 1, ..., n знайти такі, запис яких співпадає з останніми цифрами запису їх квадрату. Наприклад, 6 (
 ),
25 (
),
25 (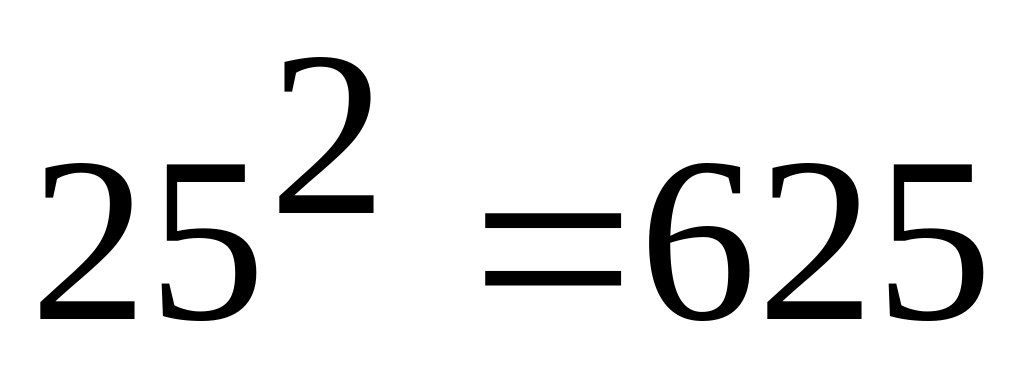 )
і т.д.
)
і т.д.Натуральне число, що складається з n цифр є числом Армстронга, якщо сума його цифр, піднесених до n-го ступеня, дорівнює самому числу (наприклад,
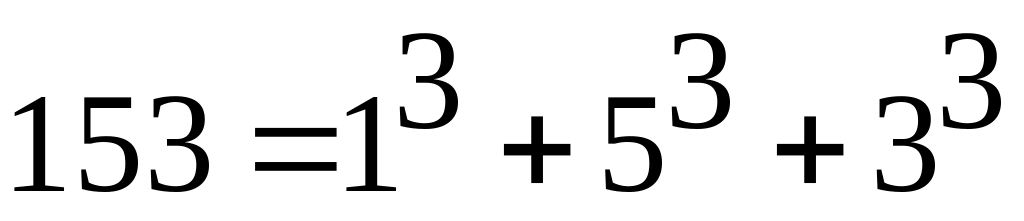 ).
Знайти всі числа Армстронга, що
складаються з 2, 3 або 4 цифр.
).
Знайти всі числа Армстронга, що
складаються з 2, 3 або 4 цифр.Дано натуральне число n. Перевірити, чи можна подати n! у вигляді добутку трьох послідовних цілих чисел.
Натуральне число називається паліндромом, якщо його запис читається однаково з початку та з кінця (наприклад, 4884, 575, 9). Знайти всі числа-паліндроми, що не перевищують 1000.
Два натуральних числа називаються дружніми, якщо кожне з них дорівнює сумі всіх дільників іншого, крім самого цього числа. Знайти всі пари дружніх чисел, що містяться у діапазоні від 200 до 300.
Дано натуральне число n. Знайти всі числа Мерсена, що не перевищують число n. Просте число називається числом Мерсена, якщо його можна представити у вигляді
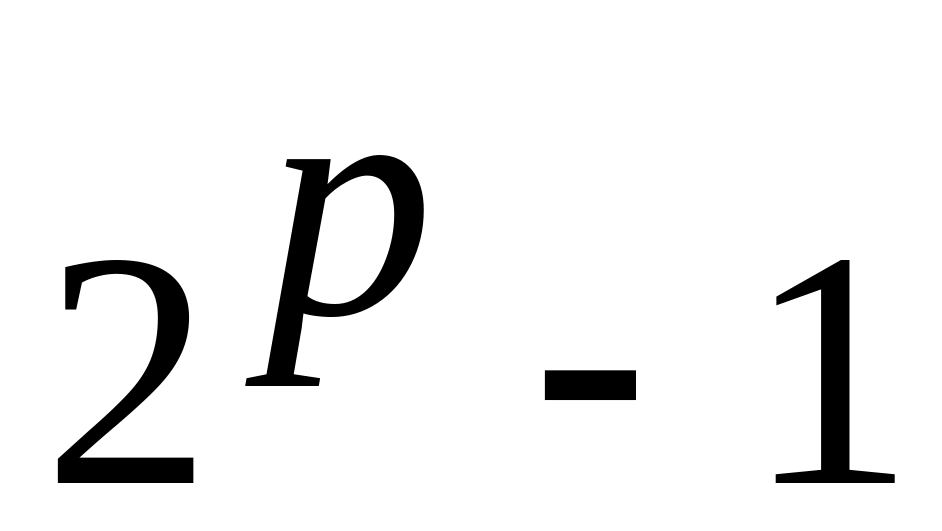 ,
де
,
де
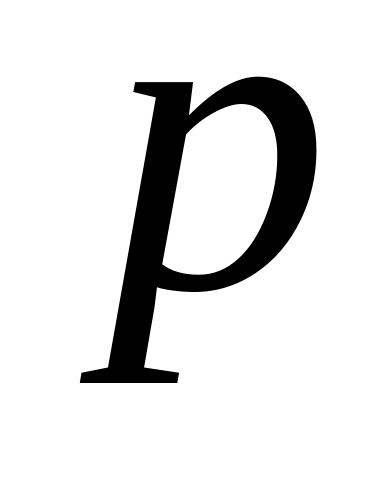 — теж просте число.
— теж просте число.Визначити усі “щасливі” шестизначні числа. Число вважається “щасливим”, якщо сума перших його трьох цифр дорівнює сумі останніх трьох цифр.
Серед тризначних чисел знайти такі, що дорівнюють сумі кубів своїх цифр.
Дано натуральне число n. Визначити всі натуральні числа, менші за n і взаємно прості з ним.
Натуральне число називається паліндромом, якщо його запис читається однаково з початку та з кінця (наприклад, 575, 9). Знайти всі числа-паліндроми, що не перевищують 100, та при піднесенні до квадрату також дають паліндроми.
Дано цілі числа p і q. Визначити всі дільники числа p, взаємно прості з q.
З чисел Фібоначі в інтервалі від 1 до 100 визначити тільки прості числа, а також їх порядкові номери в ряду Фібоначі.
Для кожного натурального числа з інтервалу [a, b] знайти всі дільники, їх кількість та суму.
Дано натуральні числа a і b (a ≤ b). Отримати всі прості числа р, які задовольняють нерівність a ≤ р ≤ b.
Ввести натуральні числа m та n. Як результат вивести усі натуральні числа, що менші за m, сума цифр яких дорівнює n.
Знайти натуральне число від 1 до n з максимальною сумою дільників.
Натуральне число називається досконалим, якщо воно дорівнює сумі всіх своїх дільників, за винятком самого себе, наприклад, 6=1+2+3. Дано натуральні числа a і b (a ≤ b). Отримати всі досконалі числа, які належать інтервалу [a, b]. Дано натуральне число n.
Отримати всі піфагорові трійки натуральних чисел, кожне з яких не перевищує n, тобто всі такі трійки натуральних чисел a, b, c, що a2+ b2= c2 (a ≤, b ≤, c ≤ n).
Для чисел, що належать діапазону [a, b], визначити ті дільники, що є членами послідовності Фібоначі.
Визначити перші 10 п’ятизначних паліндромів, що є простими числами.
Дано натуральне число m. Знайти таке натуральне число n, що двійковий запис n отримується із двійкового запису m зміною порядку цифр на зворотній.
Дано натуральне число n (n< 27). Отримати всі трьохзначні натуральні числа, сума цифр яких дорівнює n.
Отримати всі чотиризначні числа, в записі яких немає двох однакових цифр.
Дано натуральне число k, дійсне число а (а > 0). Послідовність х0, х1, х2, ..., хn утворена за законом
х0
= а,
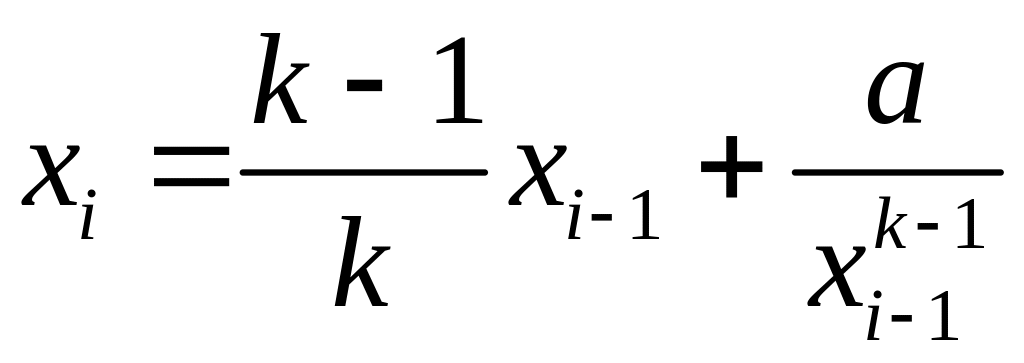 ,
і
= 1, 2, …
,
і
= 1, 2, …
Отримати
х1,
х2
+
... + х
к
,
де k
- найменше ціле число, що задовольняє
двом умовам: k
> 10,
![]() (послідовність
х1,
х2,
... сходиться до
(послідовність
х1,
х2,
... сходиться до
![]() ).
).
Для заданих цілих х і k із точністю ε = 10-5 обчислити суму
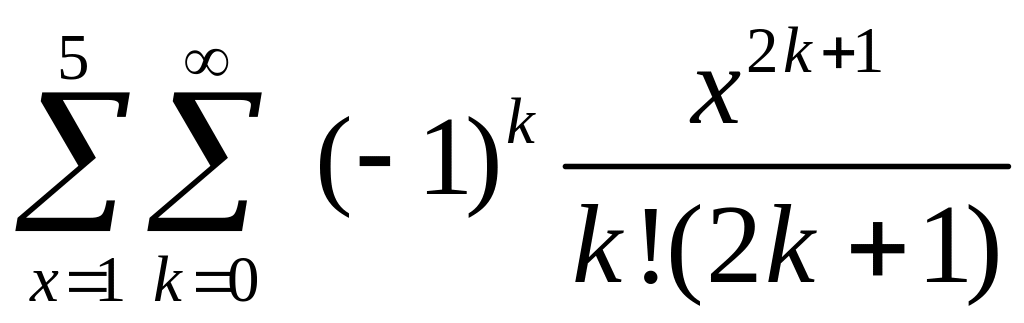
В процесі обчислення видати на екран проміжні результати.
Задане дійсне число х та послідовність а1 ,а2 ,..., an, утворена за законом
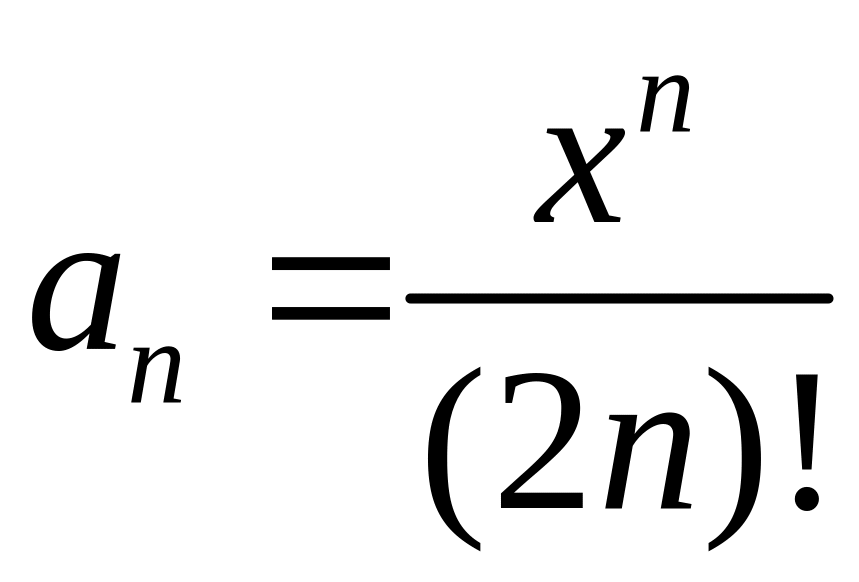 .
.
Отримати а1 + ... + ак , де k - найменше ціле число, що задовольняє двом умовам: k > 10, |ak+1 |<10-6. В процесі обчислення видати на екран проміжні результати.
Для заданих цілих х і k із точністю ε = 10-6 обчислити суму
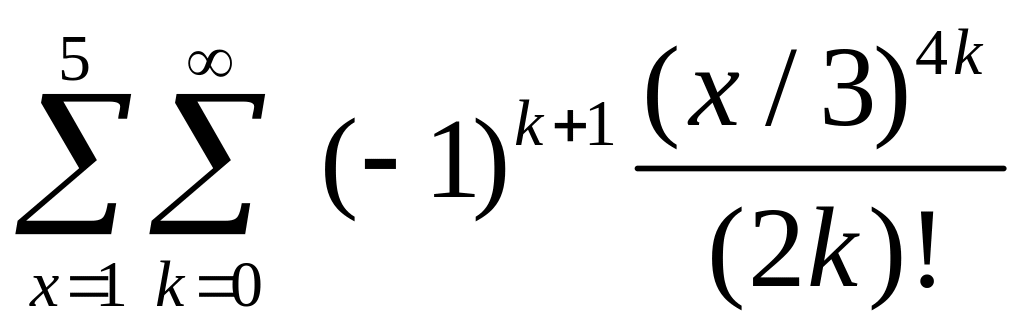
В процесі обчислення видати на екран проміжні результати.
Задане дійсне число х та послідовність а1 ,а2 ,..., an, утворена за законом
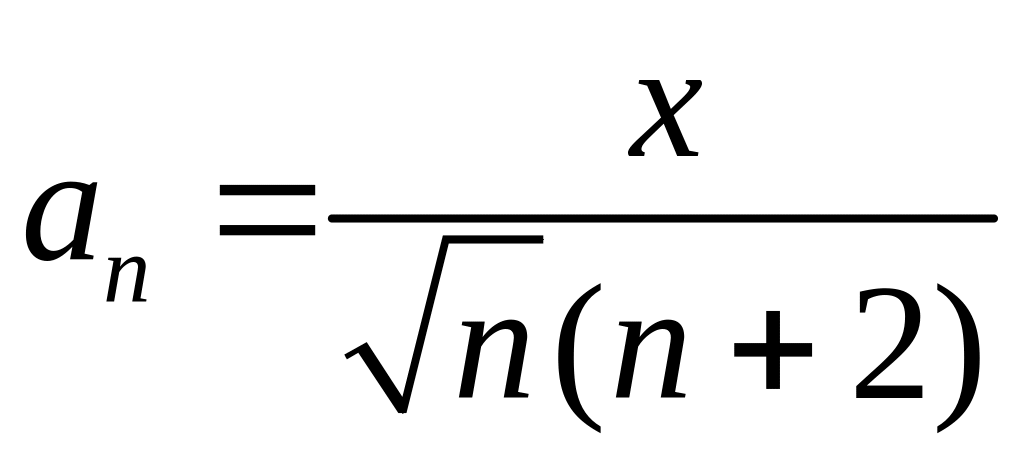 .
.
Отримати а1 + ... + ак , де k - найменше ціле число, що задовольняє двом умовам: k > 10, |ak+1 |<10-4. В процесі обчислення видати на екран проміжні результати.
