§ 4. Точность измерений и вычислений

В жизни, в практической деятельности, в научных исследованиях точность измерения физических величин занимает особое место. Какие бы измерения мы не проводили, можно смело утверждать, что проведены они с какой-то погрешностью. Невозможно измерить что-то абсолютно точно.

Приведем примеры, доказывающие это. Легко подсчитать небольшое число тел, и оно будет точным. Например, точным будет число учащихся, присутствующих на уроке, или число страниц в учебнике. Если же количество тел большое (например, число пчел в рое), то подсчитать их можно только приблизительно. Так же приближенным числом выражается число частиц пыли в единице объема воздуха. Всегда приближенными являются и числа, полученные в результате измерений. Произведя измерение, необходимо правильно оценить полученную при этом ошибку, которую называют погрешностью измерения.

Погрешность измерения зависит от правильного выбора прибора. Шкала прибора должна иметь такую цену деления, которая соответствовала бы измеряемой величине. Например, миллиметровой линейкой крайне неудобно измерять длину здания или толщину листа бумаги. В то же время этой же линейкой удобно измерять размеры книги, стола или других небольших предметов.

Кроме этого погрешность может возникнуть из-за того, что мы неправильно располагаем глаз при проведении измерений. Глаз всегда должен располагаться перпендикулярно делению шкалы, на которое мы смотрим (рис.1.11 как правильно смотреть из Жданова).

рис.1.11

Если мы поставим перед собой задачу, как можно точнее измерить длину, ширину и высоту бруска, используя линейку или измерительную ленту, у

которых разные цены делений, то точность измерения в этих случаях тоже будет разная. Длина бруска, измеренная с помощью линейки, оказалось равной 10,2 см (рис.1.10), ширина 6,4 см, а высота 5 см.

Длина этого же бруска, измеренная лентой равна 10 см, ширина 6,5 см, а высота 5 см (рис.1.12).

Р ис.1.12

Н апоминаем, что при измерении какой-либо величины мы должны принимать за ее истинное значение ту цифру на шкале, к которой ближе расположен указатель или штрих деления. Например, на рис.1.13 видно, что длина бруска равна 10,2 см или 10,3 см, но не 10,25 см.

рис.1.13

Из рис.1.14 видно, что температура в комнате, измеренная термометром равна 36,6 ^оС.

Рис.1.14

Определите объем воды в мензурке, объем тела, погруженного в воду, температуру воды (рис. 1.15).

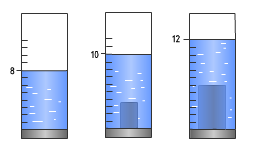
Рис.1.15

Каковы же тогда длина, высота и ширина бруска на самом деле? Для того чтобы ответить на этот вопрос необходимо ввести два новых понятия: абсолютная и относительная погрешность измерения.

Под абсолютной погрешностью измерения понимают величину, равную половине цены деления шкалы прибора.

В нашем случае абсолютная погрешность линейки равна , а для измерительной ленты абсолютная погрешность будет равна .

С учетом этого, значения величин (длины, ширины и высоты бруска) измеренных нами с помощью линейки будут равны , и соответственно. Эти же значения, но измеренные с помощью измерительной ленты будут равны , и . Видно, что во втором случае измерения произведены с большей погрешностью.

Абсолютная погрешность недостаточно наглядно оценивает точность измерения. В самом деле, если бы мы, измеряя длину бруска, ошиблись на 1 см, то измерение пришлось бы признать очень плохим. Если бы мы допустили такую же ошибку при измерении длины комнаты, то измерение надо было бы признать хорошим. То есть, точность измерения определяется не только абсолютной погрешностью, но и численным значением измеряемой величины. Поэтому вводят понятие относительной погрешности.

Под относительной погрешностью понимают величину, показывающую какую долю от измеряемой величины составляет абсолютная погрешность. Она равна отношению абсолютной погрешности к численному значению измеряемой величины.

В нашем случае относительная погрешность длины, ширины и высоты бруска при измерении линейкой соответственно равны:

.

Относительную погрешность можно выражать и в процентах, т.е. , и . Во многих случаях измерение считается удовлетворительным, если относительная погрешность не превышает 1%. При проведении измерений в школьных условиях допускается относительная погрешность (3-5) %.

В случае измерения измерительной лентой относительные погрешности соответственно равны:

Относительная погрешность дает нам возможность оценить, при измерении какой величины допущена самая большая ошибка. В нашем случае наиболее неточно измерена высота, т.к. ее численное значение наименьшее. А вот длину мы измерили с наименьшей ошибкой.

Ошибки при измерении существуют всегда. Причем ошибка измерения тем больше, чем больше цена деления. Из этого следует, что у каждого измерительного прибора существует неточность в измерениях, которая определяет класс точности прибора.

При проведении измерений любой ученик, отвлекаясь, может допустить грубую ошибку. Повторные измерения, проведенные более внимательно, укажут на этот ошибку. Это измерение надо исключить из дальнейших расчетов. Чтобы не допускать грубых ошибок, необходимо быть внимательным и аккуратным, осторожно обращаться с приборами, правильно снимать показания со шкалы приборов.

Довольно часто нам приходится не измерять, а вычислять какие-то физические величины.

Приведем такой пример. Необходимо определить объем все того же бруска, имея в распоряжении только линейку. Понятно, что для этого мы, измерив длину, ширину и высоту бруска, рассчитаем его объем по формуле и получим, что объем бруска равен

.

Найдем относительную погрешность при вычислении объема. Она будет равна сумме относительных погрешностей допущенных при измерении длины, высоты и ширины бруска, т.е.

.

Абсолютная погрешность при вычислении объема бруска будет равна

.

Тогда объем бруска, вычисленный по формуле по результатам измерений, произведенных с помощью линейки равен . Данная запись означает, что численное значение объема бруска может принимать значения от 318,9 см³ до 333,9 см³, и все они будут считаться верными. Если отложить эти значения на числовой оси, то мы получим картину, изображенную на рис.1.16а.

Если произвести аналогичные измерения при помощи измерительной ленты, то результаты вычислений будут следующими: объем бруска равен , относительная погрешность измерения , т.е. составляет 11,3%, а абсолютная погрешность в этом случае равна . Тогда объем бруска равен .

Если отложить эти значения на числовой оси, то мы получим картину, изображенную на рис.1.16б.

р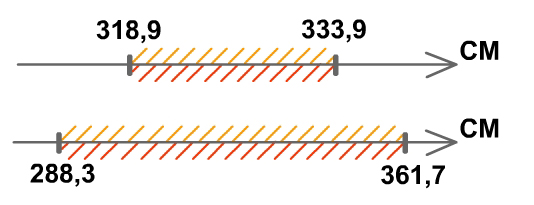 ис.1.16а и 1.16б

Получаем, что объем бруска составляет 325 см³ с возможным отклонением в большую или меньшую сторону до 36,7 см³, т.е. 288,3 см³ и 361,7 см³.

Если бы в результате измерения оказалось, что высота бруска равна , а длина и ширина остались прежними, то в этом случае объем бруска был бы равен

Но записать мы его можем только с точностью до десятых, т.е. , так как цена деления шкалы линейки позволяет проводить измерения с точностью только до десятых долей сантиметра. Поэтому объем бруска, вычисленный по результатам измерений линейкой, будет равен , а не .

Существует еще один метод определения погрешности измерения. Его называют методом границ. Пусть в нашем распоряжении имеется мензурка с ценой деления 5 мл. Допустим, что при измерении объема воды, налитой в эту мензурку открытая поверхность воды установилась между делениями 155 мл и 160 мл. Тогда измеренный объем воды находится как величина равная полусумме верхней и нижней границы измерений: . Абсолютную ошибку измерений в этом случае находится как полуразность верхней и нижней границы измерений:

.

Абсолютная погрешность в этом случае тоже оказалась равна половине цены деления шкалы прибора. Истинное значение измеряемого объема в нашем случае будет находиться в интервале от 155 мл до 160 мл. Результат измерений запишется так: .

В дальнейшем при проведении измерений и вычислений мы будем пользоваться методом границ.

В старших классах мы познакомимся с другими методами определения ошибок измерений и вычислений, а так же с самой теорией ошибок.

Вопросы для самоконтроля:

1. Что такое погрешность измерения?

2. Какая погрешность называется абсолютной?

3. Какая погрешность называется относительной?

4. Что понимают под промахом? Как избавиться от промахов?

5. Объясните, каким образом можно измерить величину наиболее точно?