Термодинамические потенциалы

План лекции: Термодинамический потенциал. Изохорно-изотермический потенциал или свободная энергия Гельмгольца. Применение энергии Гельмгольца в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Изобарно-изотермический потенциал или свободная энергия Гиббса. Применение энергии Гиббса в качестве критерия направления самопроизвольного процесса и равновесия в закрытых системах. Характеристические функции: внутренняя энергия, энтальпия, свободная энергия Гельмгольца, свободная энергия Гиббса. Уравнения Гиббса-Гельмгольца. Химический потенциал.

Термодинамический потенциал – это функция состояния системы, убыль которой в процессе, протекающем при постоянстве двух параметров, равна максимальной полезной работе.

Энергия Гельмгольца как изохорно-изотермический потенциал.

Для изохорно-изотермических условий V = const, T = const. Вспомним, что объединенное уравнение, выражающее первый и второй законы термодинамики, имеет следующий вид: .

Так как при V = const, = 0, получим

. (6.1)

Проинтегрируем данное уравнение:

.

Введем обозначение F – это энергия Гельмгольца.

F = U - TS (6.2)

Тогда F₂ = U₂ - TS₂ и F₁ = U₁ - TS₁.

, или

То есть энергия Гельмгольца – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса: В общем случае для обратимого и необратимого процессов справедливо выражение

(6.3)

Энергия Гельмгольца равна , отсюда

U = F+TS. (6.4)

То есть F – это та часть внутренней энергии, которая может быть превращена в работу, поэтому она называется свободной энергией; произведение TS – это энергия, которая выделяется в виде тепла, поэтому она называется связанной энергией.

Энергия Гельмгольца как критерий возможности протекания процесса. Дифференцируя выражение получим dF = dU – TdS - SdT . Подставляя вместо произведения TdS его выражение из «объединенного» уравнения TdS ≥ dU+pdV получим

dF ≤ - SdT - pdV. (6.5)

Так как SdT = 0 и pdV= 0 (при Т = const и V= const), тогда для изохорно-изотермических условий

(dF)_v,T ≤ 0. (6.6)

В закрытых (замкнутых) системах при изохорно-ихотермических условиях:

• если dF < 0, то процесс протекает самопроизвольно;

• если dF > 0, то процесс не протекает;

• если dF = 0, то система находится в состоянии равновесия.

Энергия Гиббса как изобарно-изотермичесий потенциал. Для изобарно-изотермических условий р = const , T = const. Преобразуем объединенное уравнение первого и второго законов термодинамики:

как (6.7)

Проинтегрируем это выражение:

или

.

Введем обозначение

- это энергия Гиббса. (6.8)

Тогда

, ,

То есть энергия Гиббса G – это термодинамический потенциал, так как его изменение равно полезной работе при протекании обратимого процесса в системе. Для необратимого процесса В случае для обратимого и необратимого процесса справедливо выражение

(6.9)

Энергия Гиббса равна , но Поэтому

отсюда . (6.10)

Энергия Гиббса G – эта часть энтальпии, которая может быть превращена в работу; поэтому она называется свободной энергией.

В выражение для энергии Гиббса подставим энергию Гельмгольца, которая определяется как F= U - TS. Тогда получим, что

или . (6.11)

Энергия Гиббса, как критерии возможности протекания процесса.

Продифференцируем выражение , получим

Вместо TdS подставим его значение из объединенного уравнения первого и второго законов термодинамики Тогда

или

(6.12)

В изобарно-изотермических условиях и

. (6.13)

То есть dG является критерием возможности протекания процесса в замкнутой (закрытой) системе в изобарно-изотермических условиях. При этом

• если dG < 0, то процесс протекает самопроизвольно;

• если dG > 0, то процесс самопроизвольно не протекает;

• если dG = 0, то система находится в состоянии равновесия.

Характеристической функцией называется такая функция состояния системы, посредством которой или ее производных могут быть выражены в явной форме термодинамические свойства системы. Характеристическими функциями являются:

1. внутренняя энергия U ,

2. энтальпия H,

3. изохорно-изотермический потенциал F,

4. изобарно-изотермический потенциал G,

5. энтропия S.

Определим значение частных производных основных характеристических функций.

Известно, что для любой функции от переменных её полный дифференциал может быть представлен выражением

,

где - частные производные этой функции по соответствующей переменной при сохранении постоянного значения остальных переменных.

Из объединенного уравнения первого и второго закона термодинамики: выводим выражение для изменения внутренней энергии:

. (6.14)

Дифференцируем выражение

Н = U + pV: .

Вместо подставляем выражение (6.14), получаем

(6.15)

Таким образом, из уравнения (6.14) следует, что а из уравнения (6.15) - .

Запишем выражение полных дифференциалов dU и dH.

(6.16)

. (6.17)

Сопоставляя уравнение (6.16) с уравнением (6.14) и уравнение (6.17) с уравнением (6.15) можно заключить, что

, (6.18, 6.19)

, . (6.20, 6.21)

Эти соотношения показывают физический смысл частных производных внутренней энергии и энтальпии.

Запишем выражения для полных дифференциалов энергии Гельмгольца и энергии Гиббса: , .

Рассмотрим F как функцию от T и V, а G как функцию T и р. Их полные дифференциалы равны:

, (6.22)

. (6.23)

Сопоставляя эти выражения с уравнениями (6.5): и (6.12): приходим к выводу, что

, , (6.24, 6.25)

, . (6.26, 6.27)

Изменение изохорного потенциала с изменением температуры при постоянном объеме определяется энтропией. Изменение изохорного потенциала с изменением объема при постоянной температуре определяется давлением.

Изменение изобарного потенциала с температурой при постоянном давлении определяется энтропией. Изменение изобарного потенциала с изменением давления при постоянной температуре определяется объемом.

Уравнения Гиббса-Гельмгольца. Запишем выражения для энергии Гельмгольца и энергии Гиббса:

.

Подставим в эти уравнения, вместо энтропии равные ей производные потенциалов, получаем соотношения:

.

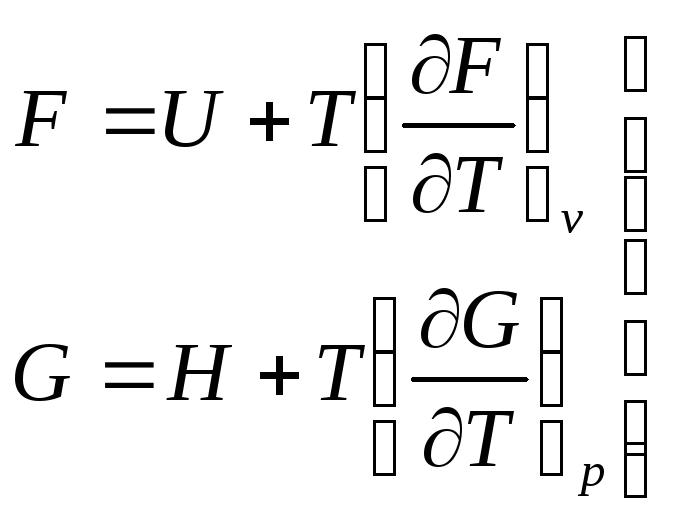Для изменения этих функций в результате процесса получим:

. (6.28, 6.29)

Уравнения (6.28 и 6.29) - это уравнения Гиббса-Гельмгольца.

Химический потенциал. Для изучения растворов и гетерогенных систем, состоящих из 2-х и более веществ необходимо рассматривать системы, где состав и масса могут быть непостоянными вследствие химической реакции, испарения, кристаллизации и т.д. Изобарный потенциал является функцией не только Т и р, но и количества n₁, n₂, n₃,…, n_j молей компонентов.

,

(6.30)

Химический потенциал вещества в смешанной фазе равен его парциальному изобарному потенциалу. Он численно равен приращению изобарного потенциала раствора, происходящему при добавлении одного моль данного компонента к такому количеству раствора, при котором (при ) его состав не меняется.

или

При : .

Математическое выражение условия равновесия системы с переменным числом молей компонентов: … (6.31)

Представим , что из фазы α в фазу β, переходит dn₁ молей 1-го компонента.

α

β

Условие фазового равновесия для 1-го компонента:

,

,

. (6.32)

При фазовом равновесии химический потенциал каждого компонента во всех фазах одинаков.

Л е к ц и я 7