2.15. Абсолютное значение энтропии. Постулат Планка. Третий закон термодинамики

В общем случае по уравнениям (2.75), (2.56), (2.81), (2.86), (2.87) невозможно вычислить абсолютное значение энтропии системы. Такую возможность дает постулат, сформулированный Планком в 1912 г., который не доказывается и не вытекает из двух законов термодинамики. Согласно этому постулату, «Энтропия индивидуального кристаллического вещества при абсолютном нуле равна нулю (S_о = 0)».

Постулат Планка очень тесно связан с квантово-статистическим обоснованием второго закона термодинамики и вероятностной трактовкой энтропии. По своему значению он уступает I и II законам термодинамики и попытки называть его третьим законом термодинамики необоснованы.

Следует также заметить, что постулат Планка не распространяется на все твердые тела. Строго говоря, он справедлив только для индивидуальных веществ, кристаллы которых построены идеально: в кристаллической решетке все узлы заняты молекулами, атомами, ионами, правильно чередующимися и закономерно ориентированными. Такие кристаллы называются идеальными твердыми телами. Они являются предельным состоянием, абстракцией.

Энтропия реальных кристаллов, решетка которых построена в некоторой степени беспорядочно, аморфных тел больше энтропии идеальных твердых тел и соответственно при О К больше нуля. Возрастание энтропии с увеличением беспорядка в расположении частиц вытекает из положений статистической термодинамики. (Энтропия – мера беспорядка). Отсюда следует: энтропия газа > энтропии жидкости > энтропии аморфного тела > энтропии кристаллического вещества, и нет оснований полагать, что это различие исчезнет при абсолютном нуле, если бы удалось достичь этой температуры¹².

Однако, как удалось подсчитать, энтропии реальных, хорошо образованных кристаллов индивидуальных веществ при абсолютном нуле невелики.

С учетом постулата Планка уравнение (2.75) для идеального твердого тела примет вид

или . (2.88)

Из уравнения следует: если бы теплоемкость сохраняла конечное значение до абсолютного нуля, то при охлаждении до этой температуры подинтегральная функция, а следовательно, и энтропия, должна была бы увеличиваться до бесконечности. По-видимому, постулат Планка может иметь место лишь потому, что теплоемкости кристаллических веществ стремятся, как это установлено экспериментально, к нулю при приближении температуры к абсолютному нулю.

Теплоемкость изменяется пропорционально некоторой степени температуры выше первой (для многих кристаллических тел пропорционально Т ³). Поэтому подинтегральная функция уравнения (2.88) стремится к нулю быстрее, чем температура, и энтропия идеального твердого тела не только равна нулю при О К (что, строго говоря, не следует из свойств теплоемкости), но и стремится к нулю, как к пределу по мере понижения температуры

T → 0, lim S = 0.

Можно показать, что при очень низких температурах не только энтропия и теплоемкость твердых тел стремятся к нулю и перестают зависеть от температуры, но и многие другие свойства твердых тел (объем, давление насыщенного пара и др.) изменяются с температурой так, что их производные по температуре стремятся к нулю. Этим объясняется принцип недостижимости абсолютного нуля, согласно которому никакие процессы не могут снизить температуру тела до абсолютного нуля.

Этот принцип определяет содержание III закона термодинамики.

Таким образом, температура, равная абсолютному нулю, в принципе недостижима, хотя наиболее низкая температура, которая достигнута экспериментально, весьма близка к абсолютному нулю и с развитием техники эксперимента может быть снижена еще больше.

Сверхнизкие температуры достигаются последовательно до приблизительно 1 К путем испарения жидкого гелия при малых давлениях, до 0,01 К – путем адиабатического размагничивания электронно-парамагнитных кристаллических веществ и, наконец, до еще более низких температур – путем такого же размагничивания ядерно-магнитных веществ. С помощью последнего метода медь может быть охлаждена на короткое время до температуры, приближенно оцениваемой в 2∙10^–5 К (Саймон с сотрудниками, 1956).

Исходя из уравнений (2.75), (2.88), а также из уравнения

S₂ – S₁ = , (2.89)

вытекающего из (2.75) для случая агрегатного превращения вещества (Т = const, λ – скрытая теплота превращения), можно построить следующий путь вычислений абсолютного значения энтропии вещества.

Найдем энтропию газа при некоторой температуре Т.

Полагаем, что при Т = 0 К любое вещество находится в твердом состоянии. Далее нужно определить теплоемкость вещества в интервале температур от самых низких (10 К, в крайнем случае, 80 К) до точки его плавления¹³. Для многих веществ такие определения проведены и выяснилось, что теплоемкости твердых веществ практически падают до нуля еще за несколько градусов и даже десятков градусов до абсолютного нуля температуры (рис. 2.10).

Особенно резко это выражено у алмаза, для которого даже при Т = 88 К с_р = 0,03, у меди – при Т = 23,5 К с_р = 0,22 кал/град·моль.

Рис. 2.10. Типичный характер изменения теплоемкости твердых веществ

с температурой

Имея такие данные, вычисляем значения С_р /Т для различных температур выбранного интервала и получаем кривую зависимости С_р /Т = f(Т) (рис. 2.11).

Рис. 2.11. Кривая зависимости с_р / Т – Т

Затем, например, планиметром определяем величину площади под кривой в пределах от 0 до заданного значения Т. Такая площадь, как известно, и есть значение интеграла

.

Чтобы окончательно определить абсолютное значение S, нужно знать S_о. Здесь на помощь приходит постулат Планка. С его учетом уравнение (2.75), как уже было показано, принимает вид

, (2.90)

и, таким образом, позволяет вычислить абсолютное значение энтропии твердого вещества.

При переходе твердого вещества в жидкое состояние при нормальной температуре плавления энтропия возрастает на величину приведенной теплоты плавления (см. уравнение 2.89).

Нагреванию жидкости отвечает увеличение энтропии, вычисляемой по уравнению (2.75):

.

Причем в подинтегральную функцию входит теплоемкость жидкости ().

Испарению жидкости при постоянном давлении (например, при Р = 760 мм рт.ст.) и нагреванию газа до заданной температуры соответствуют увеличения энтропии, аналогичные имеющим место при плавлении твердого тела и нагревании жидкости.

Исходя из сказанного, уравнение для вычисления энтропии газа при заданной температуре Т будет иметь вид

. (2.91)

По этому уравнению можно вычислить энтропию реального газа при температуре Т и р = 760 мм рт.ст. (если испарение производилось при нормальной температуре кипения).

Для получения значения энтропии идеального газа при 760 мм рт.ст. и 25 ^оС, которое приводится в таблице стандартных величин, необходимо ввести поправку. Ее рассчитывают, сочетая уравнение состояния реального газа с уравнением

.

Величина этой поправки обычно невелика и при приближенных расчетах ее можно не учитывать.

По уравнению (2.91) можно рассчитать и энтропию вещества, находящегося при температуре Т в жидком состоянии. В таком случае исчезают два последних члена.

Если вещество в твердом состоянии имеет не одну, а две и более модификации, в правой части уравнения (2.91) добавятся соответствующие члены – прирост энтропии при переходе первой модификации во вторую, при нагревании второй модификации и т.д.

Следует заметить, что для расчета энтропии, особенно газообразного вещества, требуется выполнить серию точных и трудоемких экспериментальных исследований. Поэтому число веществ, для которых этим методом найдена энтропия, увеличивается медленно.

Энтропия веществ может быть найдена также путем квантово-статистического расчета, по результатам измерений ЭДС гальванических элементов, констант равновесия и температурным коэффициентам того и другого.

Величина энтропии сложным образом отражает всю совокупность свойств вещества в данном его агрегатном состоянии. Она зависит от молекулярной массы и увеличивается с ее ростом в ряду близких по свойствам веществ; от агрегатного состояния веществ и возрастает при переходе от твердых к жидким и особенно к газообразным; от кристаллического строения, изотопного состава и структуры молекул.

Энтропийные диаграммы состояния

Энтропия широко используется в технической термодинамике (тепло-технике) как один из важных параметров рабочего тела в тепловой машине, например водяного пара. Величины энтропий водяного пара в данном сос-тоянии вычисляются по сравнению со стандартным состоянием (Т = 25 ^оС, Р =133,3∙760 Па, n = 1 моль). На основе найденных величин S строятся так называемые энтропийные диаграммы состояния водяного пара в координатах S –T или S – H (диаграмма Молье).

На таких диаграммах, подобно диаграммам V–р, можно изобразить различные процессы, совершаемые рабочим телом тепловой машины и составляющие ее рабочие циклы.

В частности, диаграмма S – T (рис. 2.12) обладает тем преимуществом, по сравнению с диаграммой V – р, что на ней изотермические и адиабатические процессы изображаются горизонтальными и вертикальными прямыми линиями.

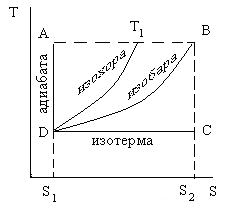
Рис. 2.12. Энтропийная диаграмма состояния водяного пара

Величина работы цикла Карно определяется площадью прямоугольника АВСД, а теплоты Q₁ и Q₂ – площадями прямоугольников АВ S₂S₁ и ДС S₂S₁.

Отсюда КПД тепловой машины

.