
Указания по решению.
На данной схеме есть m=2 узла: А и В. Сходящиеся в них токи одинаковы, поэтому первое правило Кирхгофа в данном случае дает лишь одно уравнение (m – 1=2 – 1=1, например, для узла В):
![]() .
.
Т.к.
число ветвей в данной цепи р=3,
то независимых контуров в схеме будет
![]() :
АСDB
и ABNM,
они являются элементарными контурами
цепи. В направлении указания обозначений,
т.е. по часовой стрелке, выберем и
положительное направление обхода
каждого из них. Записываем еще 2 уравнения
на основе (6.2) для указанных контуров
соответственно:
:
АСDB
и ABNM,
они являются элементарными контурами
цепи. В направлении указания обозначений,
т.е. по часовой стрелке, выберем и
положительное направление обхода
каждого из них. Записываем еще 2 уравнения
на основе (6.2) для указанных контуров
соответственно:
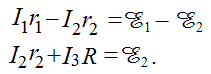
Получаем
систему из трех уравнений для искомых
сил токов в ветвях, которая, после
подстановки числовых данных из условия
задачи, принимает вид:
![]() Находим
решение этой системы: I1=2,68
А,
I2=-2,214
А,
Находим
решение этой системы: I1=2,68
А,
I2=-2,214
А,
I3=0,466 А.
Отсюда
ясно, что истинное направление тока
через второй элемент противоположно
указанному на рисунке. Падение напряжения
на зажимах реостата
![]() (В).
(В).
Задача 2
. Определите напряженность электрического поля в алюминиевом проводнике объемом V=10 см3, если при прохождении по нему постоянного тока в течение t=5 мин выделилось Q=2,3 Дж теплоты.
Указания по решению.
Количество теплоты Q, выделившейся в алюминиевом проводнике сопротивлением R при прохождении по нему постоянного тока I в течение времени t, находится по закону Джоуля-Ленца в интегральной форме:
![]() .
.
Из условия задачи не ясно, какова форма проводника, поэтому будем считать его линейным и его сопротивление считаем равным
![]() ,
,
где
![]() - удельное сопротивление алюминия
(табличная величина), l
– его длина, S
- площадь поперечного сечения, которую
считаем постоянной.
- удельное сопротивление алюминия
(табличная величина), l
– его длина, S
- площадь поперечного сечения, которую
считаем постоянной.
Искомую напряженность электрического поля в проводнике выразим:
![]() .
.
Осталось записать связь между током, напряжением на концах проводника и его сопротивлением в соответствии с законом Ома для однородного участка «данный алюминиевый проводник»:
![]() .
.
Мы рассмотрели 4 основные взаимосвязи между величинами, прямо или косвенно затронутыми в условии задачи. Попытаемся, исходя из этого, найти искомую величину. Для этого подставим в первое равенство последующие три:
 ,
,
отсюда и получается решение задачи в общем виде.
Завершите самостоятельно решение задачи, сделайте проверку размерностей и получите числовой результат.
Задача 3
Сила тока в проводнике сопротивлением R=10 Ом за время t=50 с равномерно возрастает от I1=5 А до I2=10 А. Определите: 1) заряд, протекший через поперечное сечение проводника за указанное время; 2) количество теплоты, выделившееся за это время в проводнике.
У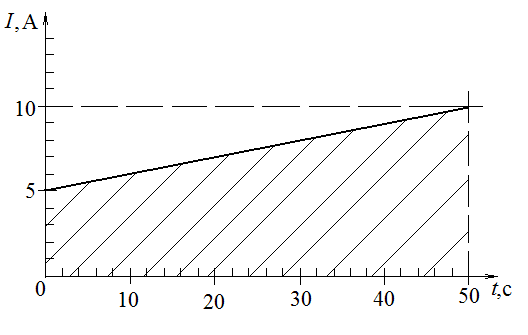 казания
по решению.
казания
по решению.
При решении этой задачи будем использовать 2 метода: графический и так называемый «метод среднего», а также аналогию с кинематикой материальной точки.
Построим график изменения со временем силы тока в проводнике (рис. 24).
1
рис. 24
I способ (графический). Известно из кинематики, что при неравномерном прямолинейном движении тела (когда скорость меняется по величине) в течение некоторого промежутка времени пройденный за это время путь графически представляется площадью криволинейной трапеции под графиком зависимости v(t) в соответствующем рассматриваемому отрезку движения временном интервале. Аналогично (с учетом таблицы 2 на стр. 70) искомый заряд равен площади заштрихованной фигуры на рис. 24, т.е. q=375 Кл.
II способ («метод среднего»). Из кинематики известно, что в случае равномерного возрастания скорости (равноускоренное движение) средняя на участке скорость равна среднему арифметическому от значений скорости в начале и в конце рассматриваемого участка движения. По аналогии найдем в данном случае среднее значение силы тока:
![]() (А).
(А).
Тогда также, как, зная среднюю скорость, находится весь пройденный путь, суммарный прошедший через поперечное сечение заряд будет равен
![]() (Кл).
(Кл).
Легко видеть, что полученные разными способами результаты совпадают.
2) Будем теперь искать количество теплоты, выделившееся за это время в проводнике.
Прежде всего, найдем искомое значение в соответствии с законом Джоуля-Ленца:
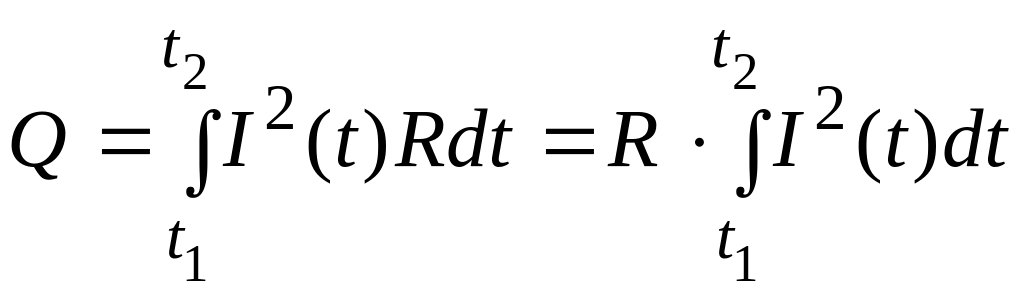 ,
(*)
,
(*)
где, согласно таблице 2, сила тока меняется по закону
![]() .
.
Подставляем и вычисляем
![]() =29,17
(кДж).
=29,17
(кДж).
