4.3.7 Модификации многопродуктовых задач развития и размещения производств.

Вариантные многопродуктовые модели задач РРП обладают большей гибкостью, позволяют отказаться от нелинейной зависимости затрат от объема производства. В таких задачах требуется выбрать из множества проектов строительства предприятий (с фиксированной специализацией, мощностью и производственными затратами) проекты, обеспечивающие полное удовлетворение потребителей по каждому виду продукции в целом по району с минимумом затрат на производство.

В дополнении к обозначениям, введенным в предыдущем разделе к безвариантной постановке, примем следующие:

пусть s ­индекс варианта строительства предприятия, так как число вариантов для различных пунктов производства различно, то ;

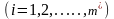i ­индекс пункта производства , причем пункты, где уже действуют предприятия, но предлагаются варианты их реконструкции или развития, обозначим , пункты нового строительства обозначим .

­ общий объем производственных затрат при реализации варианта s в пункте i;

­ объем производства продукции вида к в пункте i при строительстве по варианту s;

­ общая потребность района в к-ой продукции.

Требуется найти переменную , означающую интенсивность использования s-го варианта развития производства в i-м пункте при совокупных минимальных затратах. Величина равна единице, если вариант (проект) принимается и включается в план развития и размещения производства, и равна нулю, если вариант отвергается.

C учетом введенных обозначений модель вариантной задачи примет следующий вид:

минимизировать общую сумму производственных затрат

(4.72)

при условиях:

• общий объем производства по каждому виду продукции должен быть не меньше потребности в ней:

(4.73)

• каждый вариант должен быть принят или отвергнут целиком (условие целочисленности):

(4.74)

• для действующих предприятий обязателен выбор одного из вариантов его развития (расширения):

(4.75)

• для каждой точки нового строительства может быть выбрано не более одного (один или ни одного) из возможных вариантов:

(4.76)

В вариантной постановке многопродуктовой задачи РРП каждый из предложенных вариантов характеризуется набором показателей , задающих объем выпуска по отдельным видам продукции и в целом, и показателя , отражающего общий объем текущих (на функционирование) и единовременных (на строительство) затрат по данному варианту. Значения этих показателей определяются в результате разработки технико-экономического проекта нового строительства (реконструкции) или типовым проектом.

Целочисленность вариантной модели помогает избавиться от нелинейности. При любой форме зависимости затрат от концентрации и специализации производства критерий оптимальности всегда будет линейным, т.к. для каждого из имеющихся проектов рассчитывается один показатель общего уровня затрат , который используется в целевой функции модели в качестве постоянного коэффициента при неизвестных . Это позволяет отказаться от выделения в производственных затратах частей, зависящих от концентрации и специализации производства.

Пример 4.6. Определить оптимальный план специализации трех предприятий, выпускающих 2 вида продукции, потребность в продукции составляет 14’000 тонн и 5’000 тонн соответственно. Дополнительно данные о мощности каждого варианта предприятия и суммарных затратах на строительство приведены в таблице 4.16:

Таблица 4.16

Выпуск продукции и затраты	Пункты строительства предприятий и варианты строительства
	I		II		III
	1 вариант	2 вариант	1 вариант	2 вариант	1 вариант	2 вариант
	Х11	Х12	Х21	Х22	Х31	Х32
Выпуск продукции (тыс.т) - 1 вид продукции - 2 вид продукции	3 -	2 2	1 4	3 4	6 1	3 1
Затраты на выпуск годовой (Cis) продукции (млн.руб.)	36	40	40	59,5	56	65

Требуется найти целочисленное решение, обеспечивающее выпуск каждого вида продукции в заданном объеме с минимальными производственными затратами. Причём в пункте I обязательно строительство предприятия, а в пунктах II и III не обязательно.

Ниже (4.77÷4.79) представлена математическая модель задачи:

(4.77)

(4.78)

(4.79)

Дальнейшее усложнение экономико-математических моделей задач РРП может заключаться в сочетании многономенклатурных производств с многоэтапностями перевозок, связанными с многообразием используемых ресурсов, пунктов доставки сырья от источников сырья к каждому пункту производства и от производств к многочисленным потребителям с разными запросами. Такие задачи решаются на основе комбинации рассмотренных выше моделей.

Вопросы по теме.

1. Назначение задач развития и размещения производств.

2. Классификация задач развития и размещения производств (РРП).

3. Различия в модели простой транспортной задачи от простой одноэтапной однономенклатурной модели задачи РРП.

4. Что означает целочисленность решения задачи РРП.

5. Каким образом преодолевается в моделях задач РРП нелинейность зависимости затрат от объемов производства.

6. Составьте экономико-математическая модель к задаче раздела 4.2.7.