
- •6B050109-Математика мамандығының студенттеріне арналған
- •Пәнінің оқу-әдістемелік құралы Астана
- •Силлабус
- •Глоссарий
- •Дәрістердің қысқаша конспектісі
- •Негізгі және қосымша әдебиет тізімі;
- •Практикалық сабақтардың жоспары.
- •Еңбек көлемі есептелген білім алушының өздік жұмысының тапсырмалары;
- •Ағымдық және аралық бақылау материалдары, сонымен қатар пәнді оқып, аяқтағаннан кейінгі қорытынды бақылау материалдары
- •Семестрлік тапсырмалар
- •Жазба жұмыстарының нұсқалары
- •Өзін-өзі бақылауға арналған тест тапсырмалары
- •Бақылау жұмыстарының нұсқалары
- •Емтихан билеттерінің үлгілері
- •Емтихан сұрактары:
- •Иллюстрациялық материал (қажет болғанда);
- •Хестоматия
- •Курс жұмыстарын орындауға арналған материалдар
- •Оқу сабақтарының бағдарламалық және мультимедиялық материалдары
Бақылау жұмыстарының нұсқалары
№ 1
Түбірдің барлық мәндерін табыңыз :
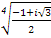
Қисықтың түрін анықтаңыз :

Берілген
 жорымал
бөлігі бойынша аналитикалық
жорымал
бөлігі бойынша аналитикалық  функциясын табыңыз.
функциясын табыңыз.Интегралды есептеңіз:
 ,
мұндағы
,
мұндағы
 :
:
Интегралды есептеңіз:
 ;
мүндағы
L:
a)
;
мүндағы
L:
a)
 ;
b)
;
b)
 ;
c)
;
c)
 ;d)
;d)

№2
Түбірдің барлық мәндерін табыңыз :

Қисықтың түрін анықтаңыз :

Берілген
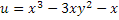 нақты
бөлігі бойынша аналити
калық
функциясын табыңыз.
нақты
бөлігі бойынша аналити
калық
функциясын табыңыз.Интегралды есептеңіз:
 где AB:
где AB:

Интегралды есептеңіз:
 мұндағы
C:
a)
мұндағы
C:
a) ;
b)
;
b)

№3
Түбірдің барлық мәндерін табыңыз :

Мына :
 теңсіздіктер арқылы анықталған облысты
сызыңыз.
теңсіздіктер арқылы анықталған облысты
сызыңыз.
![]()
Берілген
 нақты бөлігі бойынша аналити
калық
функциясын табыңыз.
нақты бөлігі бойынша аналити
калық
функциясын табыңыз.Интегралды есептеңіз:
 где L:
где L:

Интегралды есептеңіз:
 где
C:
a)
;
b)
где
C:
a)
;
b)

№4
Түбірдің барлық мәндерін табыңыз :
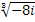
Мына
 теңсіздіктер арқылы анықталған облысты
сызыңыз.
теңсіздіктер арқылы анықталған облысты
сызыңыз.Берілген
 жорымал бөлігі бойынша аналитикалық
функциясын табыңыз.
жорымал бөлігі бойынша аналитикалық
функциясын табыңыз.Интегралды есептеңіз:
 ,
мұндағы
ABC
– сынық
сызық:
,
мұндағы
ABC
– сынық
сызық:
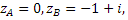
![]()
5.
Интегралды есептеңіз: ![]() мұндағы C: тік төрт бұрыш, төбелері
мұндағы C: тік төрт бұрыш, төбелері
![]()
№5
Есептеңіз:

Мына
 функция
x=1
нүктесін қайда бейнелейді.
функция
x=1
нүктесін қайда бейнелейді.

Интегралды есептеңіз:
 ,
,

№6
Есептеңіз:




Интегралды есептеңіз:
 ,
,

Емтихан билеттерінің үлгілері
№1
Комплекс саннан түбір табу амалы.
Комплекс айнымалы функциясының дифференциалдануының қажетті және жеткілікті шарттары туралы теорема.
Интегралды есептеңіз:
 ,
мұндағы
C-
контуры
,
мұндағы
C-
контуры шеңберінің жоғарғы бөлігі мен мына
шеңберінің жоғарғы бөлігі мен мына  кесіндіден құралған тұйық контур.
кесіндіден құралған тұйық контур.
№2
Комплекс сандар жазықтығы (модулі, аргументі, түйіндес комплекс сан)
Коши интегралы.
Мына
 теңдіктің геометриялық мағынасын
түсіндіріңіз
теңдіктің геометриялық мағынасын
түсіндіріңіз
№3
Комплекс сандарға амалдар қолдану.
Бөлшек-сызықтық функция
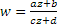 .
.Интегралды есептеңіз:
 (
( - бүтін
сан),
мұндағы
С – қабырғалары
координата өстеріне параллель центрі
а
нүктесінде болатын квадраттың периметрі
- бүтін
сан),
мұндағы
С – қабырғалары
координата өстеріне параллель центрі
а
нүктесінде болатын квадраттың периметрі
№4
Комплекс айнымалы функциясы, мысалдары.
Лаплас теңдеуі, гармоникалық функциялар.
Интегралды есептеңіз:
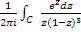 ,
егер
0
нүктесі С контурының ішінде, ал
1
нүктесі контурдан тыс орналасқан.
,
егер
0
нүктесі С контурының ішінде, ал
1
нүктесі контурдан тыс орналасқан.
№5
Комплекс айнымалы функциясының шегі
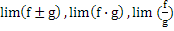
Жай контур туралы Коши теоремасы.
Берілген
 нақты бөлігі бойынша аналити
калық функциясын табыңыз.
нақты бөлігі бойынша аналити
калық функциясын табыңыз.
№6
Аналитикалық, голоморфты функциялар, мысалдар.
Комплекс айнымалы функциясының интегралын есептеу.
Мына
 теңсіздіктің геометриялық мағынасын
түсіндіріңіз
теңсіздіктің геометриялық мағынасын
түсіндіріңіз
№7
Конформды бейнелеу, мысалдар.
Коши интегралы.
Түбірдің барлық мәндерін табыңыз :

№8
Комплекс сандар тізбегінің шегі.
Функция
Интегралды есептеңіз: , егер 1 нүктесі С контурының ішінде, ал 0 нүктесі оның сыртында орналасқан
№9
Комплекс санның
 – маңайының
және шексіз алыстағы нүктенің
-
маңайының
анықтамалары.
– маңайының
және шексіз алыстағы нүктенің
-
маңайының
анықтамалары.Құрамдас контурлар туралы Коши теоремасы.
Берілген
 жорымал бөлігі бойынша
аналитикалық
жорымал бөлігі бойынша
аналитикалық
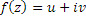 функциясын
табыңыз.
функциясын
табыңыз.
№10
Стереографиялық проекция.
2. Жай контур туралы Коши теоремасы.
3.
![]() шеңберінің
шеңберінің
![]() функциясы арқылы алынған бейнесін
табыңыз.
функциясы арқылы алынған бейнесін
табыңыз.
№11
Кеңейтілген комплекс сандар жазықтығы.
Сызықтық функция

Интегралды есептеңіз:
 ,
мұндағы
,
мұндағы

№12
Комплекс сандар қатары, жинақты және жинақсыз қатарлар, мысалдары.
Туындының аргументінің геометриялық мағынасы .
Интегралды есептеңіз: ( n – бүтін сан), мұндағы С – жарты шеңбер
 ,
,
![]() ,
контурдың бастапқы нүктесі
,
контурдың бастапқы нүктесі
![]()
№13
Абсолют жинақты қатарлар, жинақталатын қатарлардың қосындысы және айырымы.
Комплекс айнымалы функциясының дифференциалдануының қажетті және жеткілікті шарттары туралы теорема.
 шеңберінің
шеңберінің
 функциясы арқылы алынған бейнесін
табыңыз.
функциясы арқылы алынған бейнесін
табыңыз.
№14
Комплекс айнымалы функциясы, мысалдары.
Құрамдас контурлар туралы Коши теоремасы.
3.
Берілген
![]() жорымал бөлігі бойынша аналитикалық
функциясын табыңыз.
жорымал бөлігі бойынша аналитикалық
функциясын табыңыз.
№15
Комплекс айнымалы функциясының үзіліздігі және үзіліссіз функциялардың қасиеттері
Лаплас теңдеуі, гармоникалық функциялар.
3.
Интегралды
есептеңіз:
![]() ,
мұндағы
С-контуры
мына жарты сақинаның шекарасы
,
мұндағы
С-контуры
мына жарты сақинаның шекарасы
![]()
![]()
№16
Комплекс айнымалы функциясының туындысы, негізгі дифференциалдау ережелері.
Коши интегралы.
шеңберінің
 функциясы арқылы алынған бейнесін
табыңыз
функциясы арқылы алынған бейнесін
табыңыз
№17
Комплекс айнымалы функциясының интегралы және оның негізгі қасиеттері.
Туындының аргументінің геометриялық мағынасы .
3.
![]()
![]() теңдеуімен берілген сызықты анықтаңыз.
теңдеуімен берілген сызықты анықтаңыз.
№18
Комплекс саннан түбір табу амалы.
Коши-Риман шарты.
Мына
 теңдіктің геометриялық мағынасын
түсіндіріңіз.
теңдіктің геометриялық мағынасын
түсіндіріңіз.
№1
Есептеңіз:
Мына функция x=1 нүктесін қайда бейнелейді.
Интегралды есептеңіз: ,
№2
Есептеңіз:
Мына функциясы түзуді қандай сызыққа бейнелейді
Интегралды есептеңіз: ,
№3
Есептеңіз:
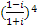
Мына функциясы
 сызықты қайда бейнелейді
сызықты қайда бейнелейді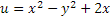
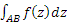 ,
,

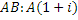 B(2+3i)
B(2+3i)
№9
Есептеңіз:




№10
Есептеңіз:


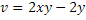

№11
Есептеңіз:
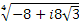
 ,
,

№14
Есептеңіз:





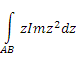
№1
Есептеңіз:


a)

b)
![]()
4.
![]()
![]()
№2
Есептеңіз:



![]()
Мына функциясы
 сызықты қайда бейнелейді
сызықты қайда бейнелейді
№3
Есептеңіз:

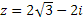

Мына функциясы сызықты қайда бейнелейді
№4
Есептеңіз:



![]()
Мына функциясы
 сызықты қайда бейнелейді
сызықты қайда бейнелейді
№5
Есептеңіз:



![]()
Мына
 функциясы
функциясы
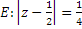 сызықты қайда бейнелейді
сызықты қайда бейнелейді
№6
Есептеңіз:



![]()
Мына
 функциясы
функциясы
 сызықты қайда бейнелейді
сызықты қайда бейнелейді
