1. Туристическая компания “Супертранс” предлагает билеты на авиарейсы.
Рейс Цена (в условных единицах)
1. Москва — Новосибирск 120 2. Москва — Иркутск 140
3. Новосибирск — Якутск 65 4. Новосибирск — Иркутск 50
5. Новосибирск — Хабаровск 80 6. Новосибирск — Владивосток 130
7. Иркутск — Якутск 30 8. Иркутск — Хабаровск 45
9. Якутск — Хабаровск 20 10. Якутск — Владивосток 80
11. Хабаровск — Владивосток 20
Начертите граф авиалиний компании и найдите в нём минимальный по стоимости маршрут из Москвы во Владивосток.
2. Дана таблица зависимости прибыли от вложений в дело различных сумм, указанных в первом столбце в проектах р1, р2 и р3.
Найдите максимальную прибыль и укажите, при каком распределении вложений она достигается.
-
Вложенная
сумма (млн. руб.)
Р1
Р2
Р3
1
0,11
0,10
0,09
2
0,12
0,14
0,12
3
0,14
0,19
0,15
4
0,18
0,21
0,29
5
0,25
0,28
0,31
3. Решите задачу о погрузке и разгрузке автомобилей на овощебазе (m=n=5):
13 9 14 |
10 11 16 |
7 4 7 |
11 15 9 |
7 8 9 7 |
15 10 |
12 13 |
6 5 |
10 16 |
9 10 12 |
14 7 |
9 16 |
8 9 |
17 14 |
10 8 5 |
6 5 |
17 17 |
7 13 |
17 9 |
6 7 7 |
8 9 |
15 12 |
15 10 |
8 11 |
9 10 9 |
4.
Функция
описывает
зависимость спроса q
от цены p.
Пользуясь свойствами эластичности,
определите коэффициент эластичности
спроса по цене. Найдите при каких
значениях цены p
спрос q
эластичен и неэластичен, при каких
значениях p
коэффициент эластичности равен 1.
5. Найдите графически коэффициенты эластичности спроса q в точках С1 и С2. Определите характер цены в точках p1 и p2.
6. Решите задачу потребительского выбора двух продуктов, цены на которые и , если бюджет потребителя равен . Функция полезности определена равенством
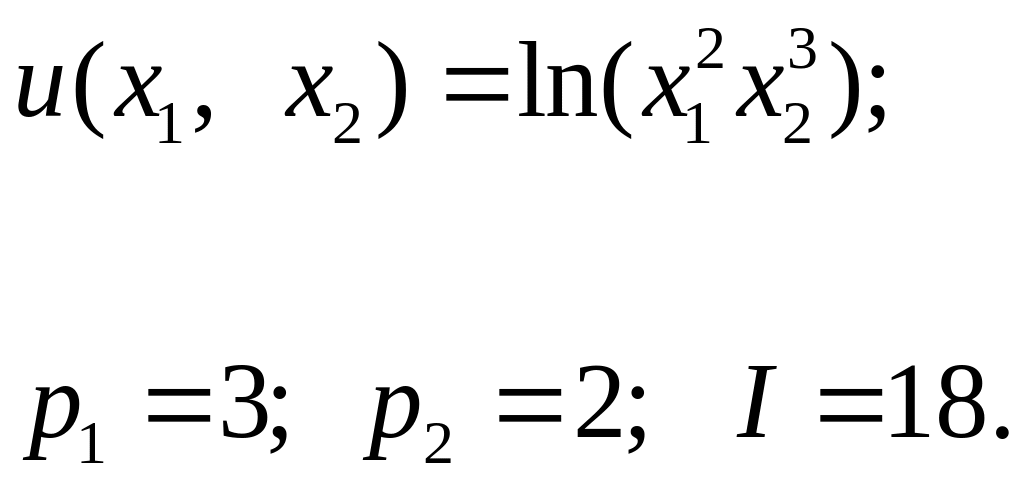
7. Построить сетевую модель и на ее основе оптимизировать распределение ресурсов с целью минимизации времени выполнения всего комплекса работ. Определить экономию времени.
Обозначение работы |
|
|
|
|
|
|
|
|
Опорная работа |
-- |
-- |
|
|
|
|
|
|
Длительность работы |
2 |
1 |
3 |
4 |
5 |
6 |
4 |
8 |
Коэффициенты пересчета |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
ВАРИАНТ № 21
1. Туристическая компания “Супертранс” предлагает билеты на авиарейсы.
Рейс Цена (в условных единицах)
1. Москва — Новосибирск 100 2. Москва — Иркутск 145
3. Новосибирск — Якутск 765 4. Новосибирск — Иркутск 50
5. Новосибирск — Хабаровск 100 6. Новосибирск — Владивосток 150
7. Иркутск — Якутск 30 8. Иркутск — Хабаровск 35
9. Якутск — Хабаровск 30 10. Якутск — Владивосток 80
11. Хабаровск — Владивосток 25
Начертите граф авиалиний компании и найдите в нём минимальный по стоимости маршрут из Москвы во Владивосток.
2. Дана таблица зависимости прибыли от вложений в дело различных сумм, указанных в первом столбце в проектах Р1, Р2 и Р3.
Найдите максимальную прибыль и укажите, при каком распределении вложений она достигается.
-
Вложенная
сумма (млн. руб.)
Р1
Р2
Р3
1
0,14
0,12
0,09
2
0,18
0,16
0,11
3
0,24
0,19
0,24
4
0,28
0,21
0,30
5
0,35
0,35
0,38
3. Решите задачу о погрузке и разгрузке автомобилей на овощебазе(m=n=5):
8 14 12 |
9 11 12 |
7 7 8 |
10 11 10 |
8 6 8 8 |
11 13 |
13 10 |
5 8 |
9 18 |
7 12 10 |
10 6 |
9 15 |
7 8 |
16 14 |
14 6 4 |
7 8 |
12 9 |
9 15 |
17 8 |
5 14 9 |
6 9 |
11 11 |
13 7 |
7 14 |
6 7 12 |
4.
Функция
описывает
зависимость спроса q
от цены p.
Пользуясь свойствами эластичности,
определите коэффициент эластичности
спроса по цене. Найдите при каких
значениях цены p
спрос q
эластичен и неэластичен, при каких
значениях p
коэффициент эластичности равен 1.
5. Найдите графически коэффициенты эластичности спроса q в точках С1 и С2. Определите характер цены в точках p1 и p2.
6. Решите задачу потребительского выбора двух продуктов, цены на которые и , если бюджет потребителя равен . Функция полезности определена равенством
7. Построить сетевую модель и на ее основе оптимизировать распределение ресурсов с целью минимизации времени выполнения всего комплекса работ. Определить экономию времени.
Обозначение работы |
|
|
|
|
|
|
|
Опорная работа |
-- |
-- |
|
|
|
|
|
Длительность работы |
3 |
2 |
3 |
2 |
4 |
5 |
3 |
Коэффициенты пересчета |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
ВАРИАНТ № 22
1. Туристическая компания “Супертранс” предлагает билеты на авиарейсы.
Рейс Цена (в условных единицах)
1. Москва — Новосибирск 100 2. Москва — Иркутск 170
3. Новосибирск — Якутск 60 4. Новосибирск — Иркутск 50
5. Новосибирск — Хабаровск 110 6. Новосибирск — Владивосток 160
7. Иркутск — Якутск 50 8. Иркутск — Хабаровск 40
9. Якутск — Хабаровск 30 10. Якутск — Владивосток 70
11. Хабаровск — Владивосток 10
Начертите граф авиалиний компании и найдите в нём минимальный по стоимости маршрут из Москвы во Владивосток.
2. Дана таблица зависимости прибыли от вложений в дело различных сумм, указанных в первом столбце в проектах Р1, Р2 и Р3.
Найдите максимальную прибыль и укажите, при каком распределении вложений она достигается.
-
Вложенная
сумма (млн. руб.)
Р1
Р2
Р3
1
0,11
0,13
0,09
2
0,12
0,15
0,10
3
0,18
0,19
0,19
4
0,25
0,21
0,27
5
0,30
0,28
0,34
3. Решите задачу о погрузке и разгрузке автомобилей на овощебазе(m=n=5):
14 8 11 |
11 9 13 |
7 6 4 |
11 10 9 |
6 8 10 7 |
12 10 |
12 11 |
6 7 |
10 16 |
8 11 14 |
13 7 |
9 16 |
8 9 |
18 17 |
10 7 5 |
6 6 |
15 11 |
8 13 |
14 7 |
4 9 6 |
8 9 |
19 12 |
15 8 |
8 11 |
9 9 10 |
4.
Функция
описывает
зависимость спроса q
от цены p.
Пользуясь свойствами эластичности,
определите коэффициент эластичности
спроса по цене. Найдите при каких
значениях цены p
спрос q
эластичен и неэластичен, при каких
значениях p
коэффициент эластичности равен 1.
5. Найдите графически коэффициенты эластичности спроса q в точках С1 и С2. Определите характер цены в точках p1 и p2.
6. Решите задачу потребительского выбора двух продуктов, цены на которые и , если бюджет потребителя равен . Функция полезности определена равенством
7. Построить сетевую модель и на ее основе оптимизировать распределение ресурсов с целью минимизации времени выполнения всего комплекса работ. Определить экономию времени.
Обозначение работы |
|
|
|
|
|
|
|
Опорная работа |
- |
|
- |
|
|
|
|
Длительность работы |
4 |
3 |
3 |
4 |
5 |
6 |
7 |
Коэффициенты пересчета |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
ВАРИАНТ № 23