3Лабораторна робота № 3

ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ МАХОВИКА ДИНАМІЧНИМ МЕТОДОМ

Прилади і приладдя:

1. махове колесо з тягарцями невеликої маси;

2. масштабна лінійка, секундомір.

3.1Теоретичні відомості

Момент інерції твердого тіла відносно деякої осі визначається виразом

,

де r – відстань елемента маси dm від осі (див. Лабораторну роботу №2).

В простих випадках величину моменту інерції визначають розрахунком, а в складних – експериментальним шляхом.

О дним із зручних методів визначення моментів інерції твердих тіл є динамічний метод, оснований на застосуванні теореми про зміну механічної енергії системи (див. далі). Цей метод дає можливість врахувати тертя в опóрах, що дозволяє звести до мінімуму пов’язані з ним помилки вимірювань.

Установка для визначення моменту інерції складається з маховика ^1 (маховóго колеса) МК зі шківом Ш, щільно насадженого на вал АВ, лінійки і тягарця (рисунок 3.1). Вал може вільно обертатись на опорах. На шків намотується нитка, до кінця якої прикріплений тягарець масою m. Під дією тягарця шків разом з валом і маховим колесом рівноприскорено обертається. На характер цього обертання впливають значення моменту інерції маховика, моменту інерції шківа, моменту інерції вала і сили тертя в опорах.

В початковому (верхньому) положенні потенціальна енергія тягарця

П = mgh,

де висота h відлічується від найнижчого положення тягарця. При опусканні тягарця його початкова потенціальна енергія перетворюється в кінетичну енергію обертального руху махового колеса, поступального руху тягарця, а також витрачається на виконання роботи проти внутрішніх сил тертя.

Система тіл «Земля – тягарець – колесо» є замкнутою, але наявність сил тертя всередині системи, веде до того, що механічна енергія системи не зберігається. Дія сил тертя призводить до часткового перетворення механічної енергії системи у внутрішню енергію, тобто у теплоту. Для таких систем справедлива

ТЕОРЕМА: зміна повної механічної енергії замкнутої системи, всередині якої діють сили тертя, дорівнює роботі внутрішніх сил тертя:

DЕ = А_т,

де DЕ = Е₂ – Е₁ – різниця між повною механічною енергією системи в кінцевому і початковому стані. Скористаємось цією теоремою. Повна механічна енергія Е системи в будь-який момент руху Е = К + П = К^пост + К^об +П. Кінетична енергія поступального руху тягарця , а кінетична енергія обертального руху маховика , де J – момент інерції маховика, w – кутова швидкість його обертання.

В початковому стані (положення 1) вантаж знаходиться у верхній точці і кінетична енергія системи , а її повна енергія . У кінцевому стані (положення 2), коли тягарець наблизився до свого найнижчого положення П₂ = 0, і Е₂ = К₂ + П₂ = К₂, тобто . За теоремою про зміну повної механічної енергії системи

, (3.1)

де А₁₂ = – F_т·h – робота сили тертя F_т на шляху від початкового до кінцевого положення; w та v – відповідно, кутова швидкість маховика та лінійна швидкість тягарця.

Обертаючись по інерції, махове колесо піднімає тягарець на висоту h₁ < h. Для визначення сили тертя F_т застосуємо ще раз теорему, вважаючи тепер нижнє положення тягарця за початкове, а положення на висоті h₁ – за кінцеве:

.

Ми врахували, що робота сили тертя від’ємна, а загальний шлях, на якому в даному випадку сила тертя виконувала роботу, дорівнює сумі h та h₁. Звідси

, (3.2)

і робота сили тертя в рівнянні (3.1) буде дорівнювати .

Виразимо у формулі (3.1) величини w та v через висоту h та час t руху тягарця від найвищого до найнижчого положення:

та v = a·t, звідки . (3.3)

Враховуючи також, що величина швидкості v тягарця співпадає з лінійною швидкістю руху точок на ободі шківа, виразимо v через кутову швидкість w обертання маховика та радіус r шківа:

v = w··r. (3.4)

Підставивши (3.2), (3.3), (3.4) в рівняння (3.1) і розв’язавши його відносно J, дістанемо:

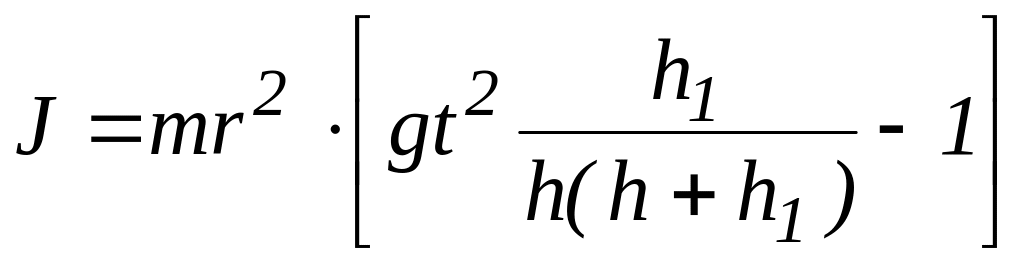. (3.5)

Відмітимо, що за умови відсутності сил тертя тобто при А_т = 0, механічна енергія системи зберігається DЕ = 0, h = h₁, і формула (3.5) набуває вигляду:

. (3.6)