От отношения угловых скоростей

Из приведённой зависимости следует, что при , прогиб вала стремится к бесконечности, т.е. прогиб вала может оказаться аварийным. После перехода через ω_кр прогиб вала у меняет свой знак (становится отрицательным) и постепенно уменьшается по абсолютному значению. Центр массы при этом все больше приближается к оси подшипников. Относительный прогиб y/e стремится к минус 1, т.е. вал самоцентрируется. Достаточно полное самоцентрирование вала имеет место при = 5 ÷ 6.

Прогиб вала считается близким к допускаемому, если удовлетворяются следующие условия виброустойчивости:

для жестких валов ;

для гибких валов .

Область является запретной.

Расчет первой критической скорости вращения вала можно вести различными приближенными методами. Наиболее распространенным является метод наложения, предложенный Донкерли. Этот метод получен на основе результатов испытаний, а позднее был обоснован и теоретически/1-3/. По Донкерли для двухопорного вала с несколькими массами (т.е. собственной массой вала и массами закрепленных на нем, мешалок, ножей, дисков) первая угловая критическая скорость ω_кр может быть определена из формулы:

(2)

где ω_кр0 – первая критическая скорость вала без дисков, рад/с; ω_крi – первая критическая скорость вала при наличии только одного i-го диска на валу, рад/с; n – число дисков на валу.

В случае вала с одним диском (n=1) первую критическую скорость можно подсчитать по формуле:

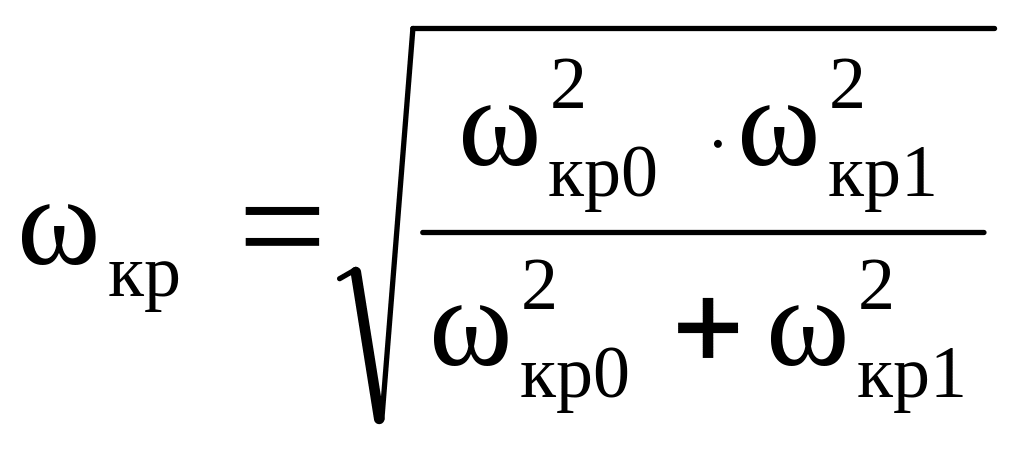(3)

Критическая скорость вала при одном диске массой m₁:

(4)

где m₁ – масса диска, кг; δ₁₁ – единичный прогиб вала (коэффициент влияния) в точке крепления диска от единичной поперечной силы, приложенной в той же точке.

Коэффициент влияния δ₁₁ для консольного вала постоянного сечения с одним диском (рис. 2) без учёта податливости опор равен:

(5)

где - момент инерции поперечного сечения вала, м⁴;

Е – модуль продольной упругости материала вала, Па;

d – диаметр вала, м.

Здесь податливостью опор (подшипников) можно пренебречь в сравнении с податливостью вала.

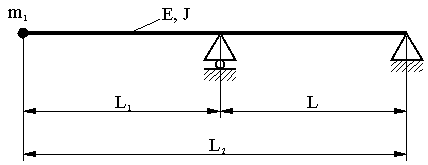
Рис. 2. Расчетная схема консольного двухопорного вала

Критическая скорость одного вала без дисков определяется по формуле:

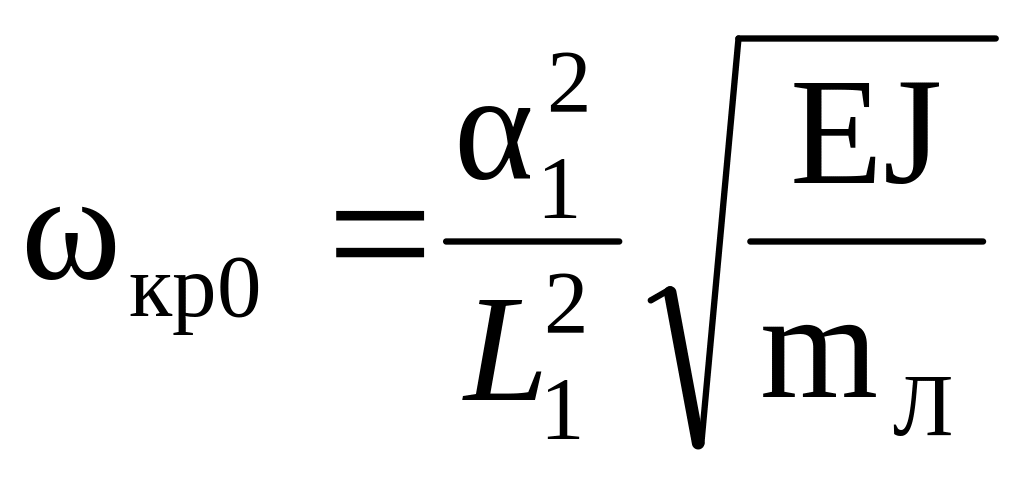(6)

где α₁ – корень частотного уравнения (дифференциального уравнения колебаний по методу акад. А.Н. Крылова);

L₁ - вылет консоли вала за подвижную опору, м;

- масса единицы длины вала, кг/м;

ρ – плотность материала вала, кг/м³.

Корни частотного уравнения α₁ для консольного вала без дисков в зависимости от отношения L/L₁ приведены в табл.1

Таблица 1

L/L1	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
α1	1,86	1,79	1,75	1,70	1,67	1,63	1,60	1,58	1,56	1,54	1,53

Приведенные выше формулы учитывают только одну нагрузку (центробежную силу) и один коэффициент влияния в точке закрепления массы диска. На критическую скорость вала при его работе могут влиять и другие факторы: гироскопический момент, положение вала в пространстве, податливость опор, наличие продольной осевой силы (растягивающей или сжимающей), крутящего момента, трения диска о окружающую среду и др.. Более подробно с данными влияниями можно ознакомиться в литературе /1-6/.