Сопряжения цилиндрической оболочки и плоского днища (б)
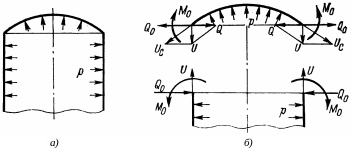
В общем случае в узле сопряжения различных элементов оболочек (например, цилиндрической и сферической) действуют внутреннее давление и равномерно распределенные по краям оболочек краевая сила и краевой момент (см. рис. 2).
В
том случае, когда имеет место соединение
частей оболочек под углом друг к другу,
в месте соединения возникает еще одна
краевая сила – распорная
сила
(она является проекцией меридиональной
силы
,
возникающей на краю оболочки под
действием давления; другой проекцией
является сила
).
Для
определения
и
составляют уравнения
совместности
радиальных
и угловых
деформаций.
При определении знаков деформаций
рассматриваются сечения оболочки,
расположенные справа от оси. При этом
используется следующее правило:
радиальные перемещения
края оболочки считаются положительными,
если под воздействием нагрузки происходит
увеличение радиуса оболочки; угловые
перемещения
считаются положительными, если поворот
края оболочки происходит по часовой
стрелке. Это правило
знаков.
(рис.
2).
Рис. 2. Схема к определению краевых сил и моментов:
а – соединение сферической и цилиндрической оболочек; б – расчетная схема;
и – меридиональные усилия соответственно цилиндрической и сферической оболочек
С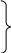
учетом этого правила для правой
относительно оси части оболочек (рис.
2, б)
составляются уравнения:
(3)
.
Индексы
«
»
и «
»
относятся к составляющим частям оболочек:
цилиндрической и сферической.
Индексы
внизу указывают, что деформации происходят
под действием соответственно давления
,
распорных сил
,
краевой силы
и краевого момента
.
Причем индексы
указывают, что деформации происходят
под действием алгебраических сумм
краевых и распорных сил, при этом
распорные силы в обеих частях оболочек
могут быть различными.
В случае если нагруженная цилиндрическая оболочка жестко закреплена в недеформирующемся основании (рис. 1), распорная сила отсутствует. При этом уравнения (3) упрощаются и с учетом того же правила знаков принимают вид:
(4)
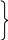
Радиальные
и угловые
деформации цилиндрической оболочки,
входящие в уравнение (4), определяются
для края оболочки (расстояние
)
по формулам 4:
;
;
;
;
(5)
;
,
где
– коэффициент Пуассона и модуль упругости
материала оболочки;
–
коэффициент затухания
.
(6)
Подставляя значения деформаций (5) в уравнения (4) и решая их, получим величину краевой силы и краевого момента :
;
.
(7)
Суммарные
меридиональные
и кольцевые
напряжения, возникающие в стенке
цилиндрической оболочки, составляют:
меридиональные
;
кольцевые (8)
,
где
,
,
,
,
,
– меридиональные и кольцевые напряжения,
возникающие в оболочке от действия
соответствующих нагрузок:
,
,
.
Знак «плюс» при напряжениях от давления и краевого момента и знак «минус» от краевой силы соответствуют указанному ранее правилу знаков.
Меридиональные и кольцевые напряжения на самом краю цилиндрической оболочки (х = 0) составляют 3, 4:
(9)
;
;
;
;
;
.
Здесь знаки напряжений от краевого момента указывают, что на внутренней поверхности оболочки волокна растянуты (+), а на наружной поверхности сжаты (–).
Напряжения
на расстоянии
от края оболочки могут быть вычислены
с учётом решения для краевой задачи 2,
4, 5.
Суммарные меридиональные и кольцевые
напряжения в соответствии с формулами
(8) для наружной поверхности экспериментальной
цилиндрической оболочки на расстоянии
от её края равны:
;
(10)
.