1.3.5. Связь способа кодирования с характером ошибки квантования

В разделе 1.2 описан случай квантования аналогового сигнала s(t), когда квантованный сигнал s_вых(t) принимает значение того или иного уровня квантования в тот момент, когда аналоговый сигнал s(t) достигает центра соответствующего интервала квантования. Ошибка квантования Е_кв в этом случае находится в пределах

где Q = 1/2^m — интервал (шаг) квантования, равный по величине младшему значащему разряду кода, которым обозначаются но­мера уровней квантования.

Такая ошибка называется ошибкой округления и обозначается символом E_Q.

Квантованию может подвергаться не только аналоговый сигнал, но и цифровой. Квантование цифрового сигнала заключается в со­кращении числа разрядов кода с некоторой величины m до величи­ны b (т >b) и является обычной процедурой в цифровых фильтрах. Поскольку любые арифметические операции с цифровыми сигна­лами являются нелинейными, результаты их могут содержать сколь угодно много значащих разрядов кода.

Сокращение их числа до некоторого значения b может осуще­ствляться двумя способами — округлением и усечением.

Округление — это замена исходного m-разрядного числа на бли­жайшее к нему b-разрядное (b<т< ∞), т. е. соответствует выбору ближайшего уровня квантования. Ошибка округления Е₀ удовлет­воряет неравенству

(1.20)

Следует заметить, что при выборе способа сокращения разрядно­сти двоичного кода (или способа квантования аналогового сигнала) ошибка квантования может зависеть от способа представления двоич­ного числа. Однако в случае округления ошибка будет одинакова для всех четырех вышеописанных кодов — прямого, обратного, дополни­тельного и смещенного. Характеристика нелинейности, соответству­ющая операции округления, показана на рис. 1.8 я. Она тождественна характеристике квантования, представленной на рис. 1.6 б.

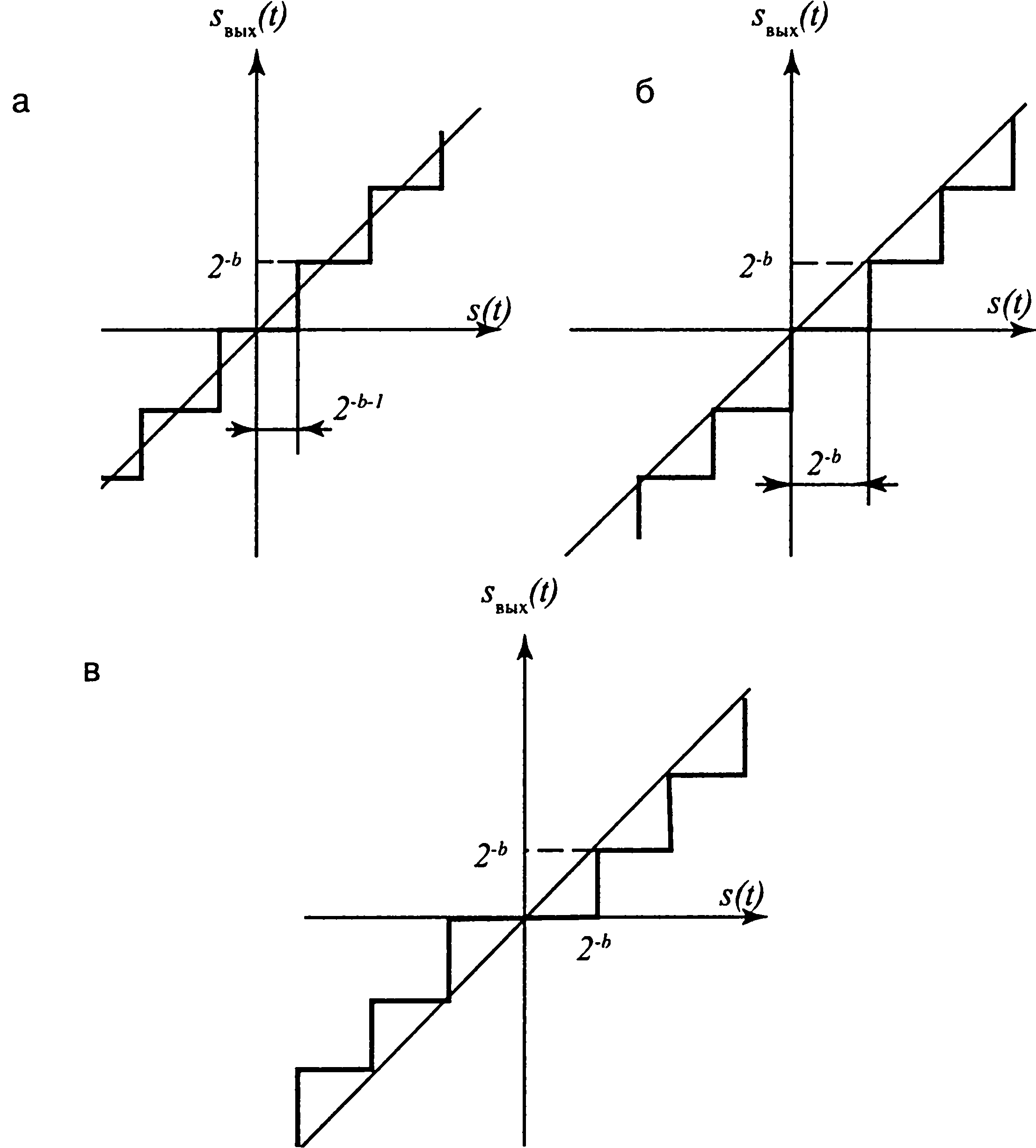
Рис. 1.8. Характеристики нелинейности квантования:

а) для операции округления; б) для операции усечения при дополнительном и смещенном кодах; в) для операции усечения при прямом и обратном кодах

Плотность вероятности ошибки округления P(E₀), в предполо­жении, что все значения ошибки равновероятны, показана на рис. 1. 9 а [3].

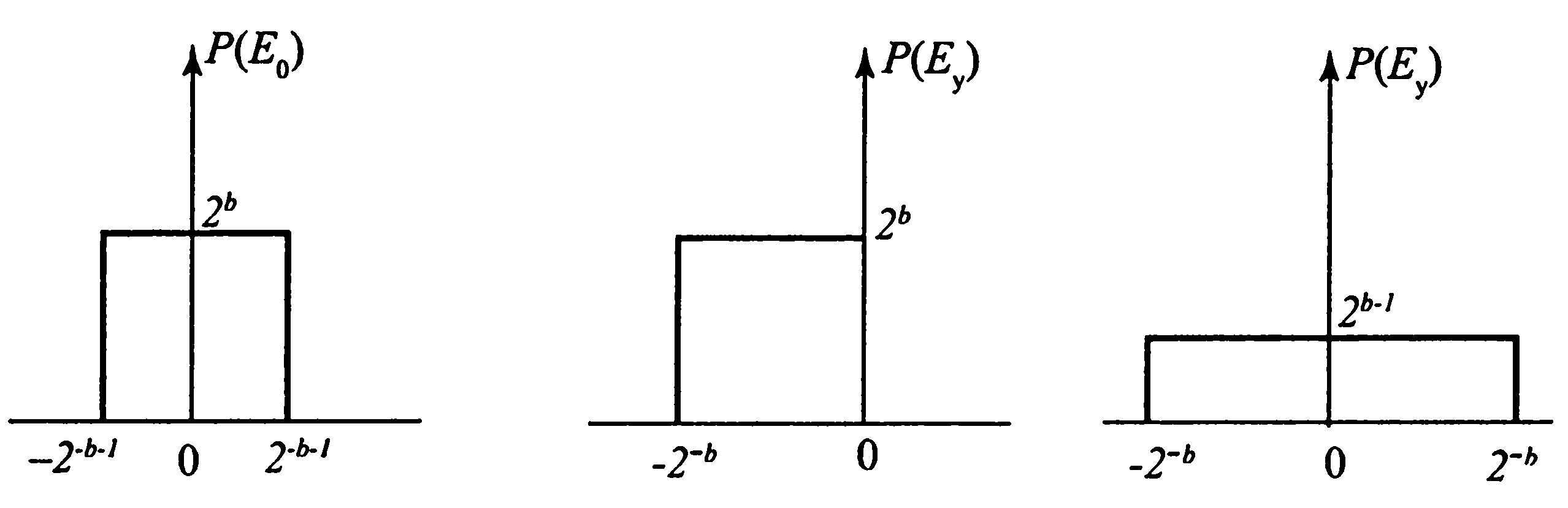
Рис. 1.9. Плотности вероятности ошибки квантования:

а) для ошибки округления; б) для ошибки усечения при дополнитель­ном и смещенном кодах; в) для ошибки усечения при прямом и обратном кодах

Усечением m-разрядного числа до b разрядов (b <т< ∞) называ­ется отбрасывание младших т-b разрядов исходного числа. При ана­лого-цифровом преобразовании усечению соответствует случай, когда квантованный сигнал принимает значение того или иного уровня квантования только после пересечения его верхней границы.

Ошибка усечения Е удовлетворяет неравенствам:

а) для положительных чисел при любом способе кодирования и отрицательных чисел в дополнительном и смещенном кодах

-2^-b ≤ Е_y ≤ 0 (1.21)

б) для отрицательных чисел в прямом и обратном кодах

0 < Е₀ < 2^-b (1.22)

В (1.21) и (1.22) считается, что m >> b.

Характеристика нелинейности, соответствующая операции усе­чения для дополнительного и смещенного кодов, показана на рис. 1.8 б, для прямого и обратного кодов — на рис. 1.8 в.

Плотности вероятности ошибки усечения Р(Е_y) показаны на рис. 1.9 б для дополнительного и смещенного кодов, и на рис. 1.9 в — для прямого и обратного кодов.