Преобразователи кодов, регистры и счетчики импульсов
1.3 Коды, используемые в ацп и цап
Цифровые данные, полученные в результате преобразования аналоговых величин, должны иметь такое представление, которое было бы «понятно» системам, обрабатывающим эти данные. Чаще всего цифровые системы оперируют с данными, представленными в прямом двоичном, обратном двоичном, двоичном дополнительном и двоичном смещенном кодах. Как правило, эти данные нормированы таким образом, чтобы все вычислительные операции выполнялись с числами, по абсолютному значению меньшими единицы:
0<|А|<1. (1.14)
Преобразуемые аналоговые сигналы в большинстве случаев являются двухполярными, поэтому при кодировании результата их преобразования код числа должен предусматривать специальный разряд, характеризующий его полярность. Этот разряд так и называется знаковым, и располагается на крайней левой позиции в записи кода.
Разрядность двоичного кода определяет точность представления числа. Если код числа имеет т+1 двоичный разряд (старший разряд — знаковый, остальные — числовые), то такой код позволяет представить 2т +1 различных чисел (2т положительных и 2т отрицательных с шагом 2-т ) в диапазоне
0<|А|< 1-2-т. (1.15)
1.3.1. Прямой код
Правила кодирования прямым кодом, который обозначается как [А]пр, следующие.
Для положительных чисел в знаковый разряд его записывается 0, для отрицательных — 1. Оставшиеся т разрядов представляют числовые разряды (дробную часть) исходного числа, причем самый младший разряд располагается на крайней правой позиции, т. е., вес разрядов возрастает справа налево в направлении к знаковому разряду.
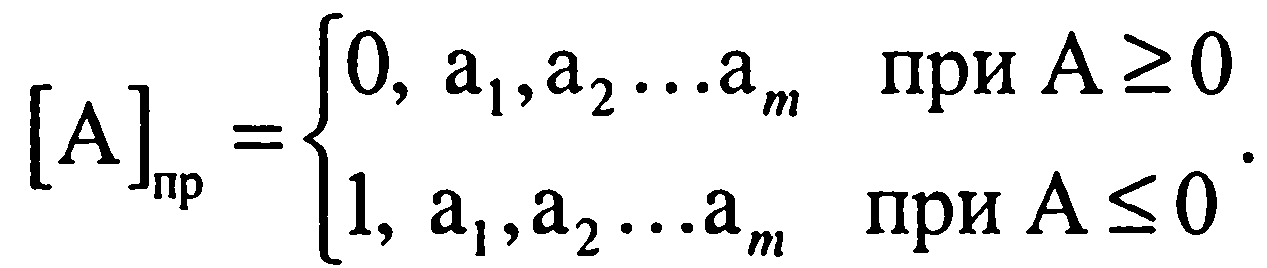(1.16)
Например, положительное число А = +0,10101 в прямом коде будет выглядеть как, [А]п = 0,10101, а равное ему по модулю отрицательное число В = -0,10101 как [В] = 1,10101.
1.3.2. Обратный код
Правила кодирования обратным кодом, который обозначается как [А]обр, похожи на правила кодирования прямым кодом , но числовые разряды отрицательных чисел здесь инвертируются
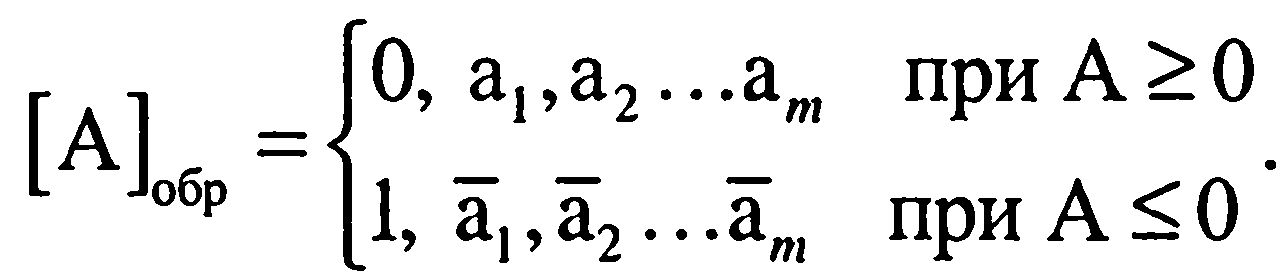(1.17)
Например, отрицательное число В=-0,10101 из предыдущего примера в обратном коде будет выглядеть следующим образом [В]обр = = 1,01010.
1.3.3. Дополнительный код
Обозначается как [А]. Правила кодирования положительных чисел те же, что для прямого и обратного кодов, т. е. [А]доп= [А]пр+[А]обр.
Правило кодирования отрицательных чисел: в знаковый разряд кода так же, как и при прямом и обратном кодировании, записывается 1; числовые разряды исходного числа инвертируются (как при обратном кодировании) и к младшему разряду прибавляется «единица»:
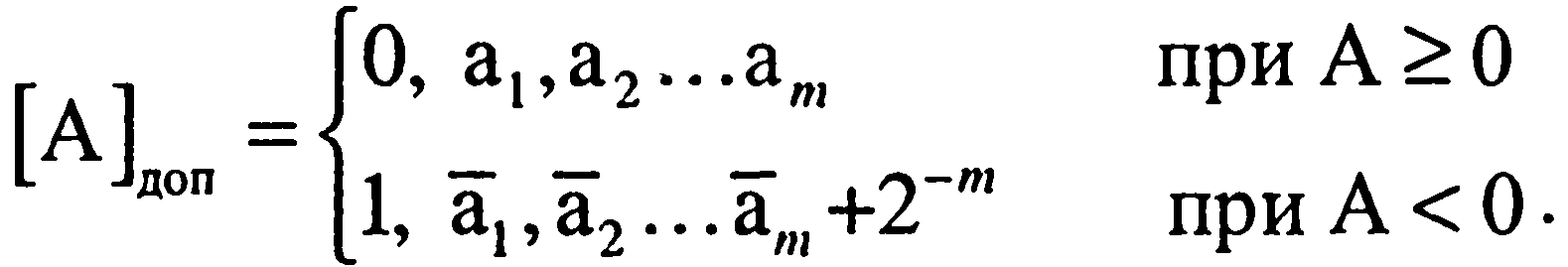(1.18)
Например,
отрицательное число В
= -0,10101 в
дополнительном коде будет выглядеть
как [В]доп
=1,
+ 1 →1,01010 + 1→1,01011.
1.3.4. Смещенный код
Этот код очень похож на дополнительный и отличается от него только обозначением знакового разряда. Если в дополнительном коде положительные числа имеют в знаковом разряде 0, а отрицательные — 1, то у смещенного кода картина противоположная: положительные числа имеют в знаковом разряде 1, а отрицательные — 0. Нулевой символ, который считается положительным числом, здесь также имеет в знаковом разряде 1. Обозначается смещенный код как [А]смещ. В остальном правила кодирования смещенным кодом те же, что и у дополнительного:
(1.19)
Например, положительное число +0,10101 в смещенном коде будет выглядеть как [В]смещ =1,10101, а отрицательное -0,10101 как
[С]смещ = 1, + 1 → 0,01010 + 1 → 0,01011.
Свое название «смещенный» код получил оттого, что вся шкала кодирования из 2т+1 чисел получается путем последовательного сдвига (смещения) первой ее половины от 0 до 2т +1 в область отрицательных значений, при этом вторая половина, начиная со значения 2т, остается в области положительных значений. Это хорошо видно из таблицы I, где представлены все четыре описанных в данной главе способа кодирования двоичных чисел.
Таблица I. Представление двоичных чисел
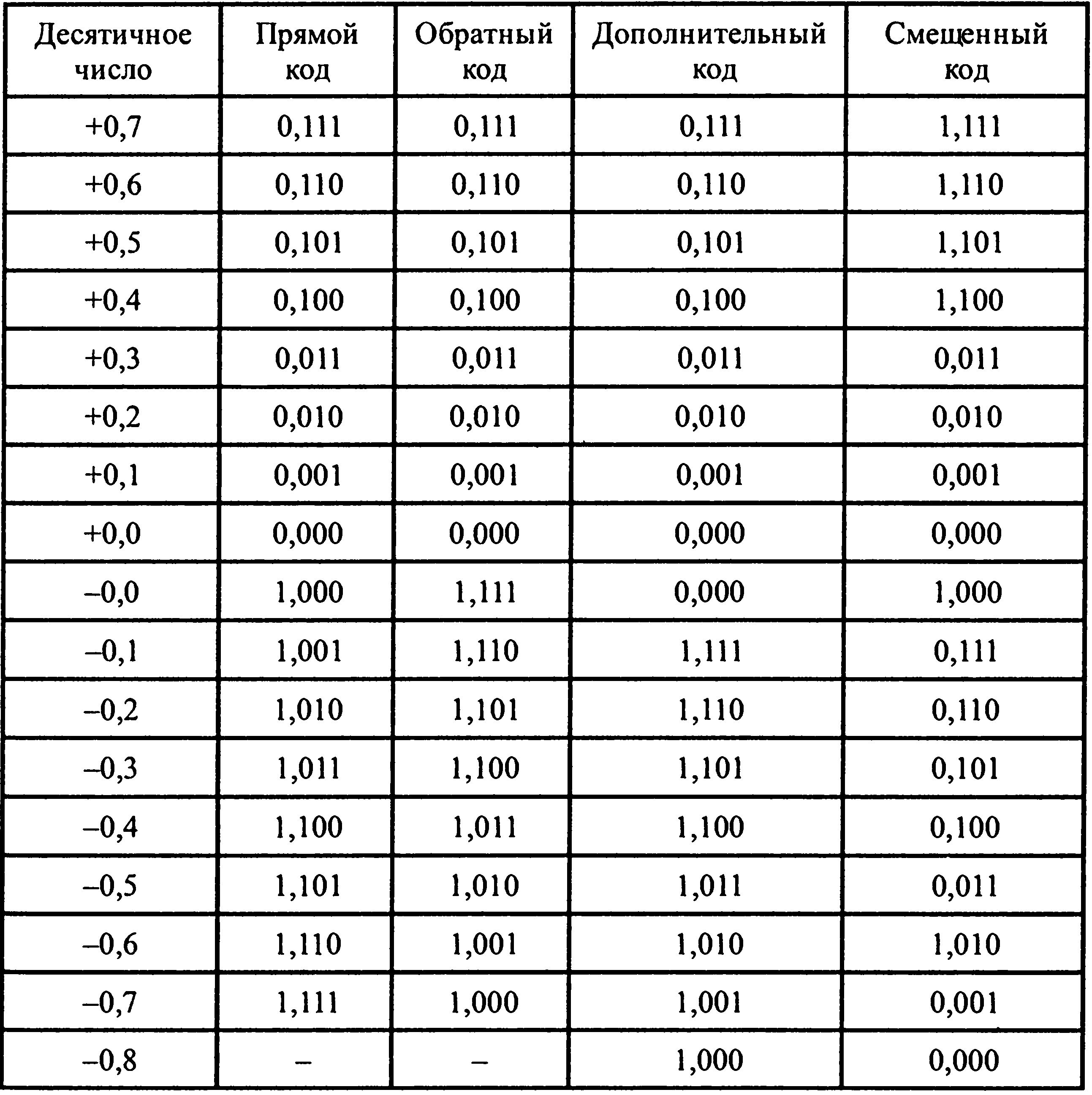
Из таблицы I также видно, что в прямом и обратном кодах «нуль» имеет двоякое обозначение, что создает известные трудности при вычислениях. Поэтому в системах цифровой обработки сигналов чаще всего используются дополнительный и смещенный коды.