Лекция 3

Квантование аналоговых величин по уровню (по значению) и дискретизация по времени. Ступень квантования и шаг дискретизации.

Прежде чем приступать к анализу процедур аналого-цифрового и цифро-аналогового преобразования, следует ознакомиться с основ­ными видами электрических сигналов, которые в дальнейшем будут служить объектами упомянутых преобразований. В самом общем случае такие сигналы можно разделить на четыре класса:

□ произвольные по величине и непрерывные по времени (рис. 1.1 а, б);

□ произвольные по величине и дискретные по времени (рис. 1.1 в);

□ квантованные по величине и непрерывные по времени (рис. 1.1 г);

□ квантованные по величине и дискретные по времени (рис. 1.1 д).

Рис. 1.1. Основные виды сигналов: а) непрерывный (произвольный) по величине и непрерывный по времени; б) кусочно-непрерывный по величине и непрерывный по времени; в) произвольный по величине и дискретный по времени; г) квантовый по величине и непрерывный по времени; д) квантовый по величине и дискретный по времени

Сигналы s(t) и s '(t) показанные на рис. 1.1а и рис 1.1б, принадлежат одному классу и чаще всего называются аналоговыми, поскольку их можно толковать как электрическое отображение реальных физи­ческих процессов. Аналоговые сигналы задаются по оси времени на несчетном множестве точек и являются непрерывными или конти­нуальными. По оси ординат такие сигналы также могут принимать любые значения в определенном интервале. Однако, как показано на рис 1.1.б, функция s '(t) в принципе может иметь и разрывы в некото­рых точках (t₁ на рис 1.1б), поэтому из двух определений — «анало­говые» и «континуальные» для такого рода функций наиболее кор­ректным было бы определение «континуальные». Тем не менее в дальнейшем изложении для обозначения сигнала s(t), произвольного по величине и непрерывного по времени, будем пользоваться бо­лее привычным для специалистов термином «аналоговый».

Сигнал S(nT), показанный на рис. 1.1 в, также, как и аналого­вый, может принимать любые значения по оси ординат, но по оси времени он определен только для некоторых фиксированных то­чек, т. е. является функцией дискретной переменной {пТ}, где п = 0, 1, 2, а Т— интервал дискретизации. Такой сигнал называется дискретным, причем в данном случае термин «дискретный» ха­рактеризует не сам сигнал, а способ его задания на временной оси. Дискретные не квантованные по амплитуде сигналы использу­ют в системах связи с амплитудно-импульсной модуляцией (АИМ).

Сигнал, показанный на рис. 1.1 г, задан на всей временной оси, однако величина его может принимать только дискретные значе­ния. В подобном случае говорят о сигнале, квантованном по уров­ню. Чтобы отличить дискретность сигнала по уровню от дискрет­ности по времени, термин «дискретный» будет применяться только к дискретизации по времени, дискретность же по уровню будет ха­рактеризоваться термином «квантование».

Квантование используют в том случае, когда необходимо преоб­разовать сигнал в цифровую форму. Для этого весь диапазон измене­ния величины сигнала разбивают на счетное число уровней и каждо­му уровню присваивают определенный номер, который затем кодируют двоичным кодом с конечным числом разрядов. Величина сигнала из­меряется в заданных точках на оси времени. Такой сигнал—дискрет­ный по времени и квантованный по уровню, называется цифровым. Он показан на рис. 1.1 д.

Возможность восстановления аналогового сигнала по его дискретным значениям.

Последовательность преобразования аналогового сигнала в цифровой

Рассмотрим в качестве примера преобразование некоторого произвольного аналогового сигнала s(t), спектр которого S(iω) ог­раничен частотой ω_макс , в цифровой сигнал s_ц(nT), где Т= 1/F_д, а n = 0,1,2...

Преобразование включает в себя три основные операции: диск­ретизацию, квантование и кодирование (рис. 1.2).

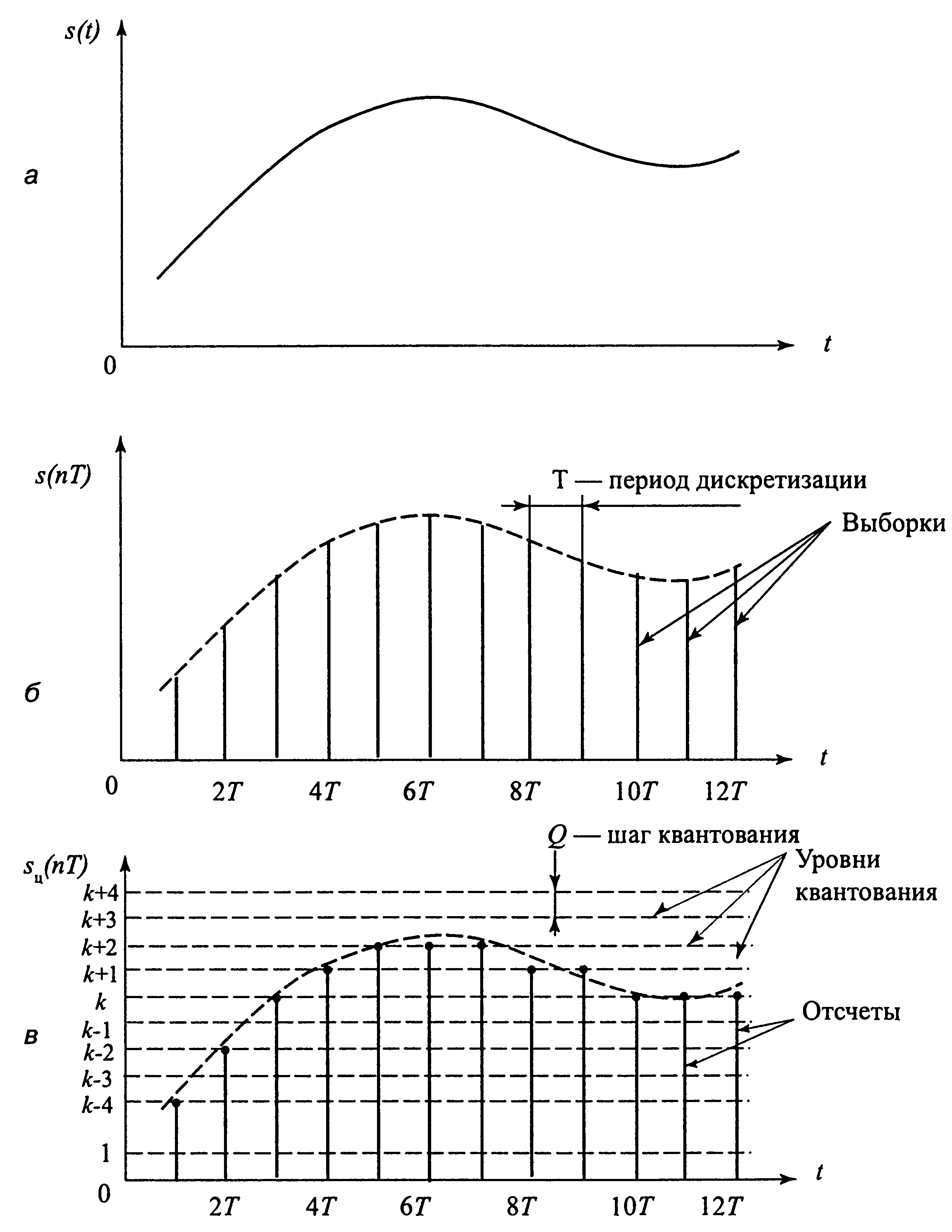
Рис. 1.2. Аналого-цифровое преобразование:

а — исходный аналоговый сигнал; б — дискретизация; в — квантование

Операция дискретизации состоит в том, что по заданному анало­говому сигналу s(t) (рис. 1.1а) строится дискретный сигнал S(nT), при­чем s(nT) = s(i). Физически такая операция эквивалентна мгновен­ной фиксации выборки из непрерывного сигнала s(t) в моменты времени t = пТ, после чего образуется последовательность выбо­рочных значений {s(nT)}. Конечно, такую дискретизацию на практике осуществить невозможно. Реальные устройства, запоминающие зна­чения аналогового сигнала (они называются устройства выборки и хранения — УВХ), не в состоянии сделать этого мгновенно — время подключения их к источнику сигнала всегда конечно. Кроме того, из-за неидеальности ключей и цепей заряда запоминающей емкости УВХ, значение взятой выборки s(nT) в той или иной степени отличается от величины исходного сигнала s(t). Тем не менее в абстрактных рассуж­дениях равенство s(t)= s(nT) считается справедливым.

Теоретически процесс дискретизации можно представить как умножение исходного сигнала s(t) на некоторую решетчатую функ­цию s(nT) с единичной амплитудой (рис. 1.3). В качестве такой фун­кции чаще всего используют дискретную дельта-функцию ((п-т)Т), которая определяется следующим образом

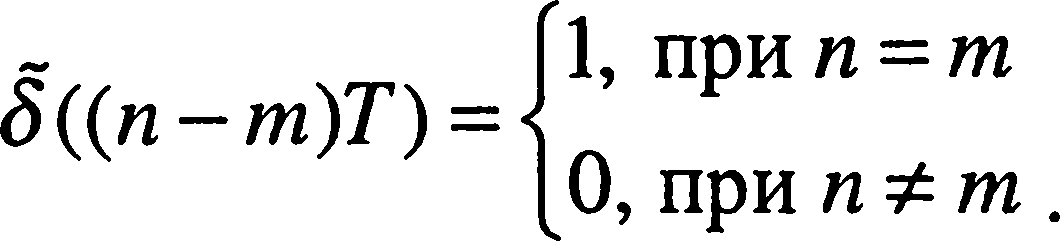
Тогда операция дискретизации будет эквивалентна амплитудной модуляции дельта-функции ((п-т)Т), функцией s(t)

Спектр S(е^iωt) полученной последовательности s(nT) выразит­ся через преобразование Фурье

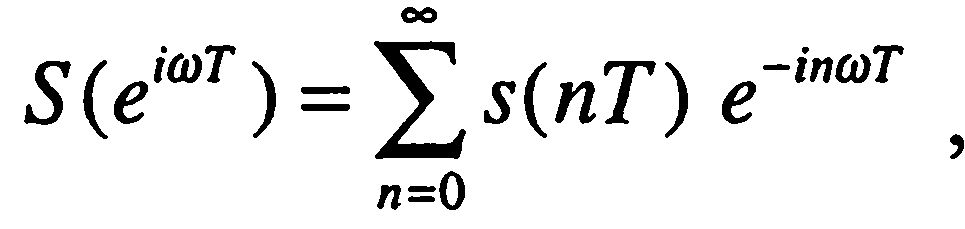(1.2)

а связь между спектрами S(е^iωt) и S(iω) дискретного сигнала s(nT) и аналогового s(t) определится формулой :

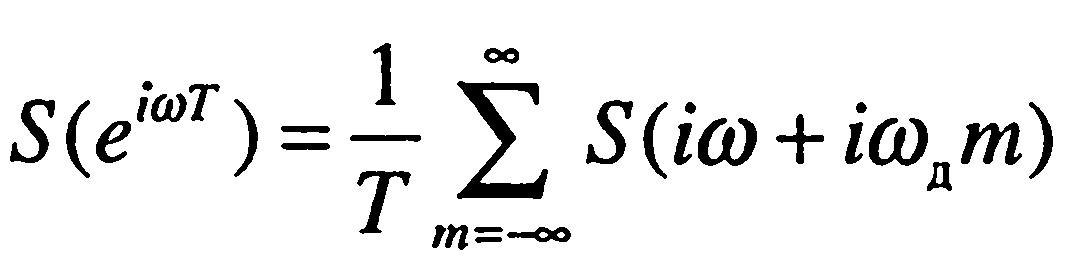(1.3)

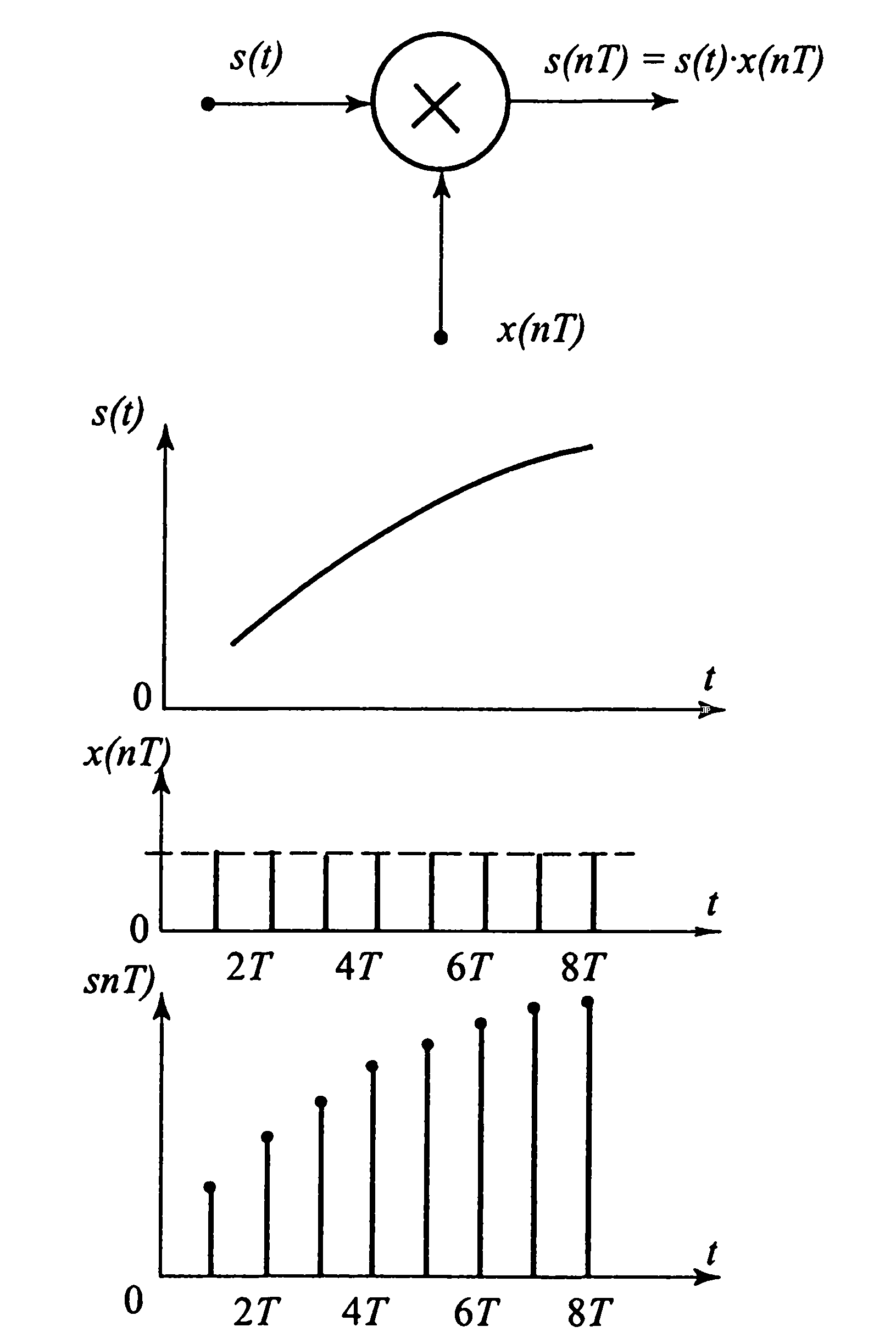
Рис. 1.3. Представление операции дискретизации сигнала S(t) в виде процесса модуляции им решетчатой функции х(пТ)

Из (1.3) следует, что после дискретизации спектр сигнала s(t) бу­дет «размножен» по оси частот в обе стороны от оси ординат, груп­пируясь вокруг частот, кратных ω_д (рис. 1.4). При этом, в зависимос­ти от знака и величины m, различают:

□ основной прямой спектр (прямая часть спектра) S⁺(e^iωT), который является частью спектра S(e^iωT) сигнала s(nT), по­лученной в итоге дискретизации аналогового сигнала s(t) и расположенной в области нижних частот от 0 до ω_д/2 = π/Т;

□ основной инверсный спектр (инверсная часть спектра) S^-(e^iωT) — это часть спектра S (e^iωT) сигнала s(nT), получен­ная в итоге дискретизации аналогового сигнала s(t) и распо­ложенная в области частот от 0 до -ω_д/2 = -π/Т;

□ сдвинутый прямой спектр (или просто прямой спектр) — часть спектра S(e^iωT), удовлетворяющая условию:

, (1.5)

где 0 ≤ ω ≤ π/Т, а k — целое число;

□ сдвинутый инверсный спектр (или просто инверсный спектр) — часть спектра S(e^iωT), удовлетворяющая условию:

, (1.6)

где 0 ≤ ω ≤ π/Т, а k —целое число.

Поскольку дискретный сигнал s(nT) в моменты времени t=nT сохраняет информацию об аналоговом сигнале s(t) и в спектре сиг­нала s(nT) содержится спектр сигнала s(t), то последний, очевидно, может быть восстановлен. Для этого дискретный сигнал достаточно пропустить через фильтр низких частот, полоса которого соот­ветствует полосе частот исходного сигнала. Тогда спектр на выхо­де такого фильтра будет идентичен спектру сигнала до дискретиза­ции.

Однако такая операция будет возможна только в том случае, если после дискретизации не произойдет перекрытия основного спектра и соседнего с ним сдвинутого. Если спектры перекроются, то в про­цессе дискретизации появится множество новых комбинаторных частот, которые попадут в полосу исходного сигнала и никакой филь­трацией избавиться от них уже не удастся (рис. 1.5).

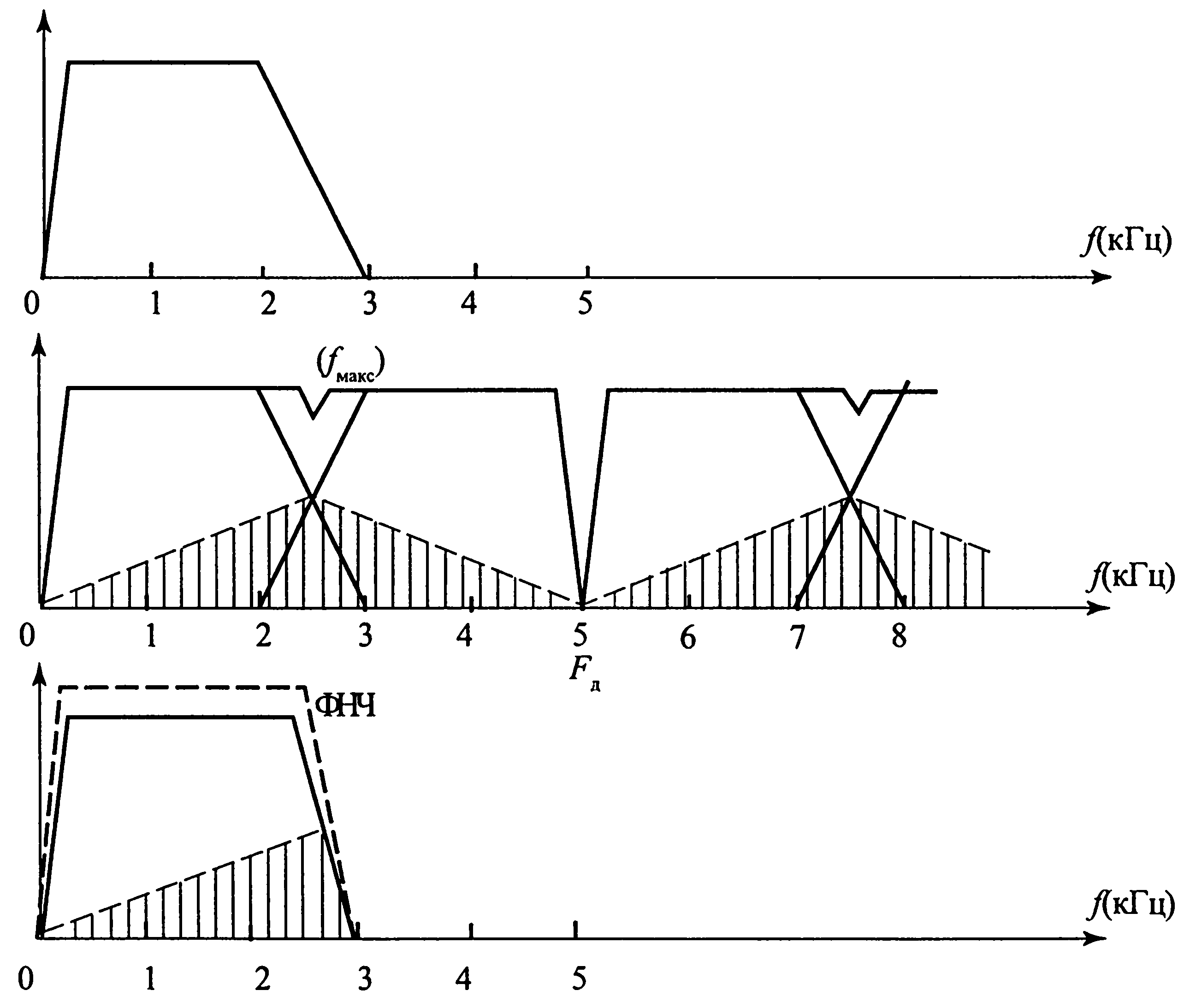
Рис. 1.5. Эффект перекрытия спектров и его последствия