2.12 Теорема Котельникова.

Эта теорема даёт условия, при выполнении которых дискретную систему можно рассматривать как непрерывную. Структурную схему дискретной САУ можно укрупненно представить в виде рисунка 1.

Рисунок 2.121. Укрупненная структурная схема САУ с екстраполятором

На рис. 1 сигнал u(t) как выходной сигнал ПКН с экстраполятором нулевого порядка представляет собой ступенчатый сигнал (рис. 2а), который можно разложить на две составляющие: непрерывный сигнал (рис. 2б) и периодический сигнал с частотой квантования , составленный из отрезков прямых (рис. 2в). ЗвеноW₀(p) служит фильтром низких частот для сигнала u(t). Если звено W₀(p) будет пропускать только непрерывный сигнал, то САУ можно рассматривать как непрерывную систему и использовать для ее разработки методы непрерывных систем. О фильтрующих свойствах звена можно судить по АЧХ (рис.3).

Теорема. Если АЧХ объекта управления можно ограничить частотой * и считать, что правее этой частоты АЧХ = 0, то систему можно рассматривать как непрерывную, при частоте квантования *.

Теорема иллюстрируется рисунками 2, 3.

а)

б)

в) ИСПРАВИТЬ!!!

Рисунок 2.12.2. Разложение ступенчатого сигнала на составляющие

Рисунок 2.12.3. АЧХ объекта управления

2.13 Устойчивость движения дискретных сау

Как и для непрерывных САУ (см. подраздел 1.9), необходимым и достаточным условием асимптотической устойчивости дискетных систем является затухание собственных движений, т.е.

, (2.13.1)

где у_с, у_в – собственная и вынужденная составляющие движения.

Характер переходных процессов определяется корнями характеристического уравнения исследуемой системы. Пусть характеристическое уравнение имеет порядок m и z₁, z₂, …, z_m простые корни характеристического уравнения. Теория разностных уравнений дает следующее решение разностного уравнения:

(2.13.2)

Корни характеристического уравнения можно представить в виде

(2.13.3)

Модуль .

Теорема. Для того чтобы дискретная система была асимптотически устойчива, необходимо и достаточно, чтобы модули всех корней ее характеристического уравнения были меньше единицы.

Для того чтобы дискретная САУ была неустойчива, достаточно, чтобы модуль хотя бы одного корня был больше единицы.

Для того чтобы дискретная САУ была на границе устойчивости, необходимо и достаточно, чтобы у части корней модули равнялись единице, причем среди них не должно быть кратных, а модули остальных корней должны быть меньше единицы.

Этой теореме можно дать геометрическую интерпретацию с помощью рис. 1 и дать другую формулировку.

Imz

-1

Рисунок 2.13.1. Расположение корней на плоскости z

Теорема. Для того чтобы дискретная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения находились внутри окружности единичного радиуса.

Для того чтобы дискретная система была неустойчива, достаточно, чтобы хотя бы один корень характеристического уравнения находился вне окружности единичного радиуса.

Для того чтобы дискретная система была на границе устойчивости, необходимо и достаточно, чтобы часть корней характеристического уравнения находились на окружности единичного радиуса, причем среди них не должно быть совпадающих, остальные должны находиться внутри окружности.

Для исследования устойчивости дискретных систем очень удобно использовать - преобразование. Вводится новая переменная по зависимостям

. (2.13.4)

w - преобразование переводит внутренность окружности единичного радиуса (А) (см. рис.1) в левую полуплоскость комплексной переменной(см. рис.2). Саму окружность (С) переводит в ось Im, а внешнюю область по отношению к окружности (В) в правую полуплоскость.

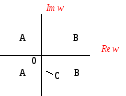
Рисунок 2.13.2 Расположение корней на плоскости w

В результате этого для исследования устойчивости дискретной системы можно использовать все критерии устойчивости, разработанные для линейных непрерывных систем.

Пример: Исследовать на устойчивость систему с характеристическим уравнением

. (2.13.5)

Сделаем -преобразование, получим

приведем это уравнение к общему знаменателю.

,

или

А_w w² + B_ww + C_w = 0 (2.13.6)

где

А_w = 1-A+B; B_w = 2(1-B); C_w = 1+A+B (2.13.7)

Для асимптотической устойчивости уравнения с характеристическим уравнением (6), необходимо и достаточно, чтобы выполнялись условия

А_w>0, B_w>0, C_w>0. (2.13.8)

Область устойчивости в параметрах А, В системы с характеристическим уравнением построена на рис. 3.

Построим область устойчивости в плоскости параметров А, В, используя соотношения (7), (8).

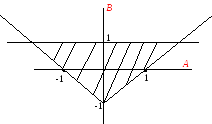
Рисунок 2.13.3. Область устойчивости на плоскости параметров АВ

Дискретная система с характеристическим уравнением (6) будет иметь в качестве области устойчивости внутренность треугольника.

Для исследования дискретной системы частотными методами надо ее передаточные функции, записать через оператор сдвига z. Затем воспользоваться -преобразованием (4). В результате получим передаточную функцию дискретной системы, выраженную через оператор, а для данных передаточных функций можно использовать частотные критерии устойчивости, разработанные для непрерывных систем.