8 Класс
Зачёт № 1
Глава I. Рациональные дроби (сентябрь, октябрь)
П.1. Вопросы:
Какие выражения называют целыми (дробными)? Приведите примеры.
Дайте определение рациональных выражений.
Какие значения называют допустимыми значениями переменных?
О каких выражениях говорят, что они не имеют смысла?
Какую дробь называют рациональной? Приведите примеры.
П.2. Вопросы:
Какое равенство называют тождеством? Приведите примеры.
Какие выражения называют тождественно равными?
Что называют тождественным преобразованием выражения?
Сформулируйте и докажите основное свойство дроби.
Сформулируйте правило об изменении знака перед дробью.
П.3. Вопросы:
Сформулируйте правило сложения (вычитания) дробей с одинаковыми знаменателями. Приведите примеры.
П.4. Вопросы:
Сформулируйте правило сложения (вычитания) дробей с разными знаменателями.
Какие множители составляют наиболее простой общий знаменатель дробей, которые складывают (вычитают)?
П.5. Вопросы:
Как умножают рациональные дроби? Приведите примеры.
Сформулируйте и докажите правило возведения дроби в степень.
П.6. Вопросы:
Сформулируйте правило деления рациональных дробей.
П.7. Вопросы:
Что называют преобразованием рациональных выражений?
Что должно получиться в результате преобразования рационального выражения, если указано, что его значение не зависит от значений входящих в него в него переменных?
П.8. Вопросы:
Какую функцию называют обратной пропорциональностью?
Какое множество чисел является её областью определения?
Как называется её график? Сколько точек необходимо для построения?
В каких координатных четвертях может быть расположена гипербола (в зависимости от k).
Зачёт № 2
Глава II. Квадратные корни (ноябрь, декабрь)
П.9. Вопросы:
Какие числа образуют множество рациональных чисел (натуральных, целых)? Какой буквой обозначают каждое множество?
От какого латинского слова произошёл термин “рациональное число” и что оно означает?
Как может быть представлено каждое рациональное число?
Какие десятичные дроби называют периодическими (непериодическими)?
Что называют периодом дроби? Как записывают периодические дроби?
П.10. Вопросы:
Какие числа называют иррациональными? Приведите примеры.
Какие числа образуют множество действительных чисел?
Какой буквой обозначают множество действительных чисел?
Какие действительные числа можно (какие нельзя) представить в виде отношения целого числа к натуральному числу?
П.11.Вопросы:
Сформулируйте определение арифметического квадратного корня.
Как его записывают и при каких значениях он имеет смысл?
П.12. Вопросы:
Сколько корней имеет квадратное уравнение х2 = а (в зависимости от a)?
П.13. Вопросы:
Как можно находить приближённые значения арифметического квадратного корня?
Каково приближённое значение
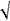2
(
3
)?
П.14. Вопросы:
Какова область определения функции y = x?
Как расположен её график в системе координат?
Что значит, что график функции проходит через точку? Сформулируйте этот вопрос иначе.
П.15. Вопросы:
Чему равен квадратный корень из произведения?
Чему равен квадратный корень из дроби?
П.16. Вопросы:
Чему равен квадратный корень из степени?
Какое тождество применяют при извлечении квадратного корня из степени с чётным показателем? Приведите примеры.
Перечислите свойства степеней с натуральными показателями (повторение).
П.17. Вопросы:
Объясните на примере, как можно вынести множитель из-под знака корня.
Объясните на примере, как можно внести множитель под знак корня.
П.18. Вопросы:
Какие преобразования выполняют с иррациональными выражениями?
Объясните на примере, как можно освободиться от иррациональности в знаменателе дроби. Какие выражения называют сопряжёнными?
Назовите способы разложения многочлена на множители.(повторение)
Зачёт № 3