
- •9. Формализм волновой механики.
- •9.1. Общие постулаты. Средние значения.
- •9.2. О дискретном и непрерывном спектрах. Проблема собственных значений.
- •9.3. Дискретный спектр.
- •9.3.1. Собственные значения и собственные функции эрмитового оператора.
- •9.3.2. Разложение волновой функции в ряд по ортонормированной системе собственных функций.
- •9.3.3. Статистическое распределение, сопоставляемое динамической переменной.
- •9.3.4. Коммутирующие наблюдаемые и совместные переменные. Полные наборы коммутирующих наблюдаемых. Чистые и смешанные состояния.
- •9.4. Алгебра коммутаторов.
- •9.4.1. Основные свойства.
- •9.4.2 Изменение статистического распределения во времени. Интегралы движения.
9.4. Алгебра коммутаторов.
9.4.1. Основные свойства.
Коммутаторы
наблюдаемых появляются в различных
конкретных вопросах квантовой механики.
Они входят в формулировки теорем (см.
например, предложение 1 п. 9.3.4), в различные
уравнения и т.п. Если мы рассматриваем
две динамические переменные 𝒜
= 𝐴(𝑞, 𝑝),
 = 𝐵(𝑞, 𝑝) и сопоставляемые им по
постулату (а) эрмитовы операторы 𝐴 и
𝐵, то вместо [𝐴, 𝐵] мы будем писать
также [𝒜,
]
или [𝐴(𝑞, 𝑝), 𝐵(𝑞, 𝑝)], например, [𝑞𝑖,
𝑝𝑖]
вместо
= 𝐵(𝑞, 𝑝) и сопоставляемые им по
постулату (а) эрмитовы операторы 𝐴 и
𝐵, то вместо [𝐴, 𝐵] мы будем писать
также [𝒜,
]
или [𝐴(𝑞, 𝑝), 𝐵(𝑞, 𝑝)], например, [𝑞𝑖,
𝑝𝑖]
вместо
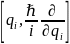 и т.п. При этом, правда, нельзя забывать
в каждом конкретном случае все о том же
вопросе о неоднозначности сопоставления
динамической переменной 𝒜 эрмитова
оператора 𝐴 (мы скоро вернемся к этому
вопросу).
и т.п. При этом, правда, нельзя забывать
в каждом конкретном случае все о том же
вопросе о неоднозначности сопоставления
динамической переменной 𝒜 эрмитова
оператора 𝐴 (мы скоро вернемся к этому
вопросу).
Предложение 1. Пусть 𝐴, 𝐵, 𝐶 – линейные операторы. Тогда:
[𝐴, 𝐵] = -[𝐵, 𝐴]; (43)
[𝐴, 𝐵+ 𝐶] = [𝐴, 𝐵]+ [𝐴, 𝐶]; (44)
[𝐴, 𝐵𝐶] = [𝐴, 𝐵]𝐶 + 𝐵[𝐴, 𝐶]; (45)
[𝐴, [𝐵, 𝐶]] +[𝐵, [𝐶, 𝐴]] +[𝐶, [𝐴, 𝐵]] = 0 (46)
 (45’)
(45’)
Доказательство. Свойства (43)-(46) проверяются непосредственно, а (45’) следует из (45).
Предложение 2.
 (47)
(47)
 (48)
(48)
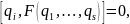 (49)
(49)
 (50)
(50)
 (51)
(51)
 (52)
(52)
Доказательство. Доказываем при помощи предложения 1.
Возвращаясь к вопросу о неоднозначности сопоставления 𝒜⟶𝐴, мы видим, что согласно предложению 2 можем решить его, предположив вперед, что функция 𝐴(𝑞1, . . . , 𝑞𝑠; 𝑝1, . . . , 𝑝 𝑠) записана в виде полинома или ряда по степеням 𝑝1, . . . , 𝑝𝑠 с коэффициентами – функциями только от 𝑞1, . . . , 𝑞𝑠. В этом случае, в частности, имеют место равенства
 (53)
(53)
 (54)
(54)
9.4.2 Изменение статистического распределения во времени. Интегралы движения.
Рассмотрим уравнение Шредингера и сопряженное ему уравнение
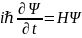 ,
,
 (55)
(55)
Пусть 𝛹 нормирована на 1 при 𝑡 = 𝑡0. Тогда она остается нормированной на 1 и при остальных 𝑡, а среднее значение наблюдаемой 𝐴 в любой момент 𝑡 задается равенством:
 (56)
(56)
Дифференцируя это равенство по 𝑡 и учитывая уравнения Шредингера (55) и эрмитовость гамильтониана, получаем:
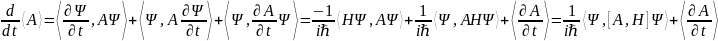 .
(57)
.
(57)
Мы получили уравнение
 .
(58)
.
(58)
Это – общее уравнение эволюции среднего значения наблюдаемой 𝐴. Ему удовлетворяет и среднее значение оператора 𝑒𝑖𝜉𝐴, то есть характеристическая функция статического распределения наблюдаемой 𝐴 (см. п. 9.3.3):
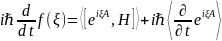 (59)
(59)
Если наблюдаемая (оператор) 𝐴 явно от времени не зависит, то второй член справа в уравнении (58) равен нулю. Если наблюдаемая 𝑐 коммутирует с 𝐻 и явно от времени не зависит, то (при 𝐴 = 𝑐) в ноль обращаются оба слагаемых справа в (58), и мы получаем:
 (60)
(60)
Итак:
если наблюдаемая 𝑐 коммутирует с
гамильтонианом и не зависит явно от
времени, то остаются постоянными во
времени и среднее значение
 ,
и характеристическая функция распределения
наблюдаемой c,
и, следовательно, само это распределение.
Такую наблюдаемую называют интегралом
движения
или постоянной
движения,
поэтому мы можем еще сказать: если
наблюдаемая коммутирует с гамильтонианом
и не зависит явно от времени, то этого
достаточно, чтобы она была интегралом
движения. В частности, если гамильтониан
явно от времени не зависит, то (так как
он коммутирует, разумеется сам с собой)
он – интеграл движения. Так как
гамильтониан, не зависящий от 𝑡 явно,
имеет смысл энергии, то этот интеграл
называют интегралом
энергии.
,
и характеристическая функция распределения
наблюдаемой c,
и, следовательно, само это распределение.
Такую наблюдаемую называют интегралом
движения
или постоянной
движения,
поэтому мы можем еще сказать: если
наблюдаемая коммутирует с гамильтонианом
и не зависит явно от времени, то этого
достаточно, чтобы она была интегралом
движения. В частности, если гамильтониан
явно от времени не зависит, то (так как
он коммутирует, разумеется сам с собой)
он – интеграл движения. Так как
гамильтониан, не зависящий от 𝑡 явно,
имеет смысл энергии, то этот интеграл
называют интегралом
энергии.
