9.3. Дискретный спектр.

9.3.1. Собственные значения и собственные функции эрмитового оператора.

Рассмотрим задачу на собственные значения

()

для линейного эрмитового оператора A в классе функций , принадлежащих гильбертовому пространству , и обсудим последовательно несколько связанных с ней вопросов.

1. Если - собственная функция оператора A, принадлежащая собственному значению a, то при любой постоянной c функция также собственная функция оператора A, принадлежащая тому же собственному значению a.

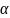2. Две нормированные на 1 собственные функции вида оператора A, принадлежащие одному и тому же собственному значению a, отличаются на множитель , где - вещественное число.

3. Максимальное число линейно независимых собственных функций , принадлежащих одному и тому же собственному значению a, называют порядком или кратностью вырождения этого собственного значения. Собственное значение кратности 1 называют невырожденным. Множество собственных функций, принадлежащих собственному значению a кратности k, образует подпространство размерности k в .

4. Все собственные значения эрмитового оператора вещественны.

5. Две собственные функции, принадлежащие различным собственным значениям, ортогональны друг другу. Отсюда следует, что они линейно независимы.

6. Применяя к линейно независимым собственным функциям , принадлежащим собственному числу a кратности , процесс ортогонализации Шмидта, всегда можно получить ортонормированную систему из собственных функций, принадлежащих тому же собственному значению a. Всякая собственная функция, принадлежащая этому собственному значению a , представима линейной комбинацией из этих собственных функций (при 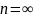линейная комбинация – это сходящийся в норме ряд Фурье).

7. Собственные значения задачи () образуют конечную или бесконечную (счетную) последовательность 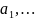изолированных вещественных чисел.

Упражнение. Дополнить приведенные свойства необходимыми доказательствами и (или) пояснениями.

9.3.2. Разложение волновой функции в ряд по ортонормированной системе собственных функций.

Пусть - конечная или счетная последовательность ортонормированных собственных функций оператора A, принадлежащих собственному значению , а – множество всех этих собственных функций, отвечающих собственным значениям . Каждая функция из удовлетворяет равенствам:

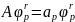, (15)

, (16)

где - символ Кронекера (равенство (16) при следует из свойства 5 п. 9.3.1).

если ортонормированная система полна в , то любая волновая функция (как функция из ) может быть представлена рядом Фурье

, (17)

причем коэффициенты Фурье

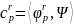(18)

удовлетворяют равенству Парсеваля (теорема Пифагора):

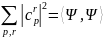(19)

Скалярное произведение двух волновых функций (как и любых двух функций из ) представляется в виде

(20)

С другой стороны, если

, (21)

то ряд 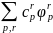сходится в к функции, имеющей норму . В частности, ряд

(22)

сходится в , если сходится ряд

. (23)

Аналогично можно определить функцию

, (24)

т.к. правая часть сходится в , если сходится ряд

. (25)

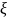Таким образом, в частности, можно определить оператор , где - вещественный параметр:

, (26)

так как

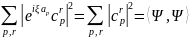(27)

для любой .
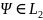