9. Формализм волновой механики.

В п.8 (и ранее в п.6.5) мы приняли как исходное положение (которого будем придерживаться и далее), что динамическое состояние квантовой системы в момент t полностью определяется заданием волновой функции в этот момент. Мы ввели и обсудили вероятностные распределения координат и импульсов квантовой системы через волновую функцию в координатном и импульсном пространствах. Мы ввели понятия средних значений (и среднеквадратических отклонений) этих координат и импульсов и обсудили, как работать с ними. В частности, мы ввели средние значения для динамических переменных - функций только координат или только импульсов. Все это означает, что мы ввели и обсудили понятия состояния квантовой системы пока недостаточно. Теперь мы хотим ввести общее понятие состояния. Для этого мы должны ввести более общее понятие статистического распределения для динамических переменных - функций координат и импульсов и обобщить для них понятие средних значений (и среднеквадратических отклонений).

9.1. Общие постулаты. Средние значения.

В п. 8.3 (см.ф.(34),(50); аналогичные формулы (35), (49) мы пока оставляем в стороне) каждой динамической переменной или мы сопоставили соответственно оператор умножения и оператор дифференцирования . Это означает, что каждой из рассмотренных динамических переменных мы сопоставили некоторый оператор (линейный) A и среднее значение . При этом мы предполагали, что нормирована на 1. В общем случае, выражение для среднего значения следует скорректировать к виду . Все это обобщают на случай произвольной динамической переменной 𝒜 - функции A (q₁, …, q_s; p₁, …, p_s) от декартовых координат и сопряженных им импульсов следующим образом ( - число степеней свободы классического анализа рассматриваемой квантовой системы).

Постулат (а). Любой динамической переменной сопоставляется линейный оператор 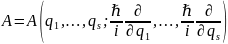(1)

Постулат (б). Если – волновая функция системы в момент t (и стало быть, ею полностью определяется состояние системы в этот момент), то среднее значение динамической переменной есть . (2)

Вспомним теперь, что в п.6.3 для получения уравнения Шредингера мы применяли принцип соответствия, по которому гамильтониану ставился в соответствие оператор . Ясно, что фактически мы тогда использовали постулат (а) (аргумент t сейчас фиксирован, но для общности его можно было бы и добавить в (1)), то есть постулат (а) – это общий принцип соответствия.

В связи с принципом соответствия, для того, чтобы избежать неединственности соответствия (тогда принцип был бы некорректен), мы дополним его в п.6.3 двумя правилами:

1) использовать только декартовы координаты;

2) из всех возможных записей функции в принципе соответствия использовать только симметризованную.

Будем придерживаться этих правил и далее (тем более, что первое из них мы уже оговорили перед формулировкой постулатов).

В связи с принципом соответствия, естественно обсудить еще один вопрос – каким вообще классам функций ограничиться при рассмотрении динамических переменных. С точки зрения здравого смысла и для упрощения математического аппарата понятия динамической переменной 𝒜 стоит насколько это возможно конкретизировать так, чтобы удобным в работе оказался и класс соответствующих линейных операторов A. В этом смысле весьма эффективным оказывается такое естественное требование, чтобы динамические переменные представляли физические (наблюдаемые) величины. Действительно, отсюда, в частности, следует, что является вещественной функцией q и p. Тогда от величины естественно потребовать, чтобы она была вещественной как среднее значение (с точностью до - см.(2)) наблюдаемой 𝒜. Короче говоря, разумно потребовать, чтобы скалярное произведение было вещественной величиной, а это в частности означает, что

(3)

для любой волновой функции .

Равенство (3), выполняемое для любой волновой функции, означает, как мы знаем, эрмитовость (самосопряженность) оператора A.

Упражнение. Если A – эрмитов оператор на пространстве волновых функций, то для любых волновых функций и выполнено равенство

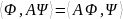(4)

или, что то же,

(5)

Замечание. Равенство (5) часто рассматривают как определение эрмитовости оператора A, а вместо вещественности исходно в постулате (а) требуют эрмитовости оператора А.