Задача 19.Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины х, заданной по данному закону ее распределения:

Х	-5	1	8	4
р	0,4	0,3	0,1	0,2

Решение. Дисперсию можно вычислить, исходя из ее определения, однако мы воспользуемся формулой

D(X) = M(X²) – [M(X)]².

Найдем математическое ожидание случайной величины Х:

M(X) = х₁р₁ + х₂р₂ + … + х_nр_n = -5∙0,4 + 1∙0,3 + 8∙0,1 + 4∙0,2 = -0,1

Напишем закон распределения для Х²:

Х2	25	1	64	16
р	0,4	0,3	0,1	0,2

Найдем математическое ожидание квадрата случайной величины Х²:

M(X²) = х²₁ р₁+ х ²₂р₂ + … + х²_nр_n,

M(X²) = 25∙0,4 + 1∙0,3 + 64∙0,1 + 16∙0,2 = 19,9.

Найдем искомую дисперсию:

D(X) = M(X²) – [M(X)]² = 19,9 – (-0,1)² = 19,89.

Найдем искомое среднее квадратическое отклонение:

.

Ответ: Дисперсия равна 19,89, среднее квадратическое отклонение равно 4,46.

Задача 20.Случайная величина Х задана интегральной функцией (функцией распределения) F(x). Требуется: 1) найти дифференциальную функцию (плотность вероятности); 2) найти математическое ожидание и дисперсию Х; 3) построить графики интегральной и дифференциальной функций.

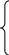0 при х ≤ 0

х² _{ПРИ 0 < x ≤ 11;}

F(x) = 121

1 при х > 11.

Примечание. Для решения задачи необходимо знать:

1. (c∙f(x))′ = c∙(f(x))′;

2. (xⁿ)′ = n∙x^n-1;

3. ∫ f(x)dx = F(x) + c;

4. ∫ c∙f(x)dx = c ∫ f(x)dx;

5. ∫ (f₁(x)+f₂(x) + … +f_n(x))dx = ∫ f₁(x)dx + ∫ f₂(x)dx + … + ∫ f_n(x)dx;

xⁿ⁺¹

6. ∫ xⁿdx = _{n + 1} + c;

_{b b}

7. ∫ f(x)dx = F(x)│ = F(b) – F(a).

^{a a}

Решение.

1) Плотность распределения вероятностей равна первой производной функции распределения:

0 при x ≤ 0

f(x) = F′(x) = 2∙x _{при 0 < x ≤ 11}

¹²¹

^{0 при x > 11}

2) Найдем математическое ожидание:

11 11 11 11

М(Х) = ∫ x∙f(x)dx = ∫ x∙2∙x /121dx = 2/121∫ x²dx = 2/121 ∙ x³/ 3 =

0 0 0 0

= 2/362 ∙ (11³ – 0³) = 22/3 = 7,3.

3) Найдем искомую дисперсию, учитывая, что М(Х) = 22/3:

_b

или D(X) = ∫ x² f(x)dx – [M(X)]^2.

^a

11 11

D(Х) = ∫ [x ]²∙f(x)dx-М²(х) = ∫ (x )² ∙2x/121dx –(22/3)² =

_{0 0}

¹¹

=2/121(x⁴/4) –(22/3)² = 6,72.

⁰

4) Построим графики интегральной и дифференциальной функций:

у

Х 0 11

F(x) 0 1

1

0 11 x

у X 0 11

f(x) 0 2/11

_2/11

0 11 x

Ответ: 1)Дифференциальная функция равна:

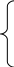
0 при x ≤ 0;

f(x) = F′(x) = 2∙x _{ПРИ 0 < Х ≤ 11;}

¹²¹

^{0 ПРИ Х > 11.}

2)Математическое ожидание и дисперсия соответственно равны: М(Х) = 7,3, D(X) = 6,72