14. Решение типовых заданий контрольной работы

Задание 1.1

В партии 30 изделий, 10 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад пяти изделий три изделия являются дефектными?

Решение. События А –среди отобранных пяти изделий, три изделия являются дефектными.

30			5
10 деф.	20 нет		3 деф.	2 нет

Общее число возможных элементарных исходов события n равно числу способов, которыми можно взять пяти изделий из тридцати, т.е. число сочетаний из тридцати элементов по пять.

.

m - число благоприятствующих исходов событию А определяется как произведение · , где первый сомножитель указывает число комбинаций выбора деталей с дефектами из десяти. Но с каждой такой комбинацией могут встретиться детали без дефектов. Число комбинаций таких деталей будет . Поэтому искомая вероятность запишется в виде ,

Р(А) = 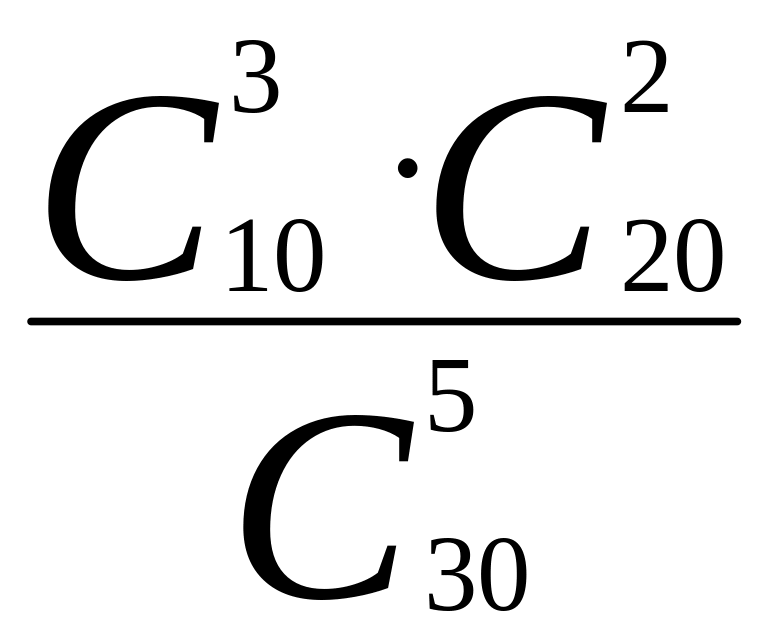= 0,16.

Ответ: Р (А) = 0,16.

Задание 1.2

На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: n₁= 20 c первого завода,n₂=1,5 со второго, n₃=15 с третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе p₁=0,9, на втором p₂=0,9, на третьем p₃=0,8. Какова вероятность того, что взятое случайным образом изделие будет качественным?

Решение. Задача решается по формуле полой вероятности:

Р(А)=Р(H₁) ^. Р(А/ H₁) + Р(H₂) ^. P(A/ H₂) + Р(Н₃) ^.Р(A/ Н₃).

Событие А - взятое изделие оказалось качественное.

Гипотезы:

H₁ - изделие первого завода;

H₂ - изделие второго завода;

Н₃ - изделие третьего завода.

На завод поступило всего изделий n = n₁ + n₂ + n₃ =50.

Вычислим вероятности данных гипотез

Р(H₁) = n₁/n =20/50= 0,4 ; Р(H₂)= n₂ /n=15/50=0,3 ;

Р(Н₃)= 15/50 = 0,3.

Условные вероятности соответственно равны Р(А/ H₁) = p₁ = 0,9,

P(A/ H₂) = p₂ = 0,9, P(A/ Н₃) = p₃ 0,8.

Искомую вероятность того, что взятое изделие окажется качественным, найдем по формуле:

Р(А)=Р(H₁) ^. Р(А/ H₁) + Р(H₂) ^. P(A/ H₂) + Р(Н₃) ^.Р(A/ Н₃) =

=04 ^. 09+0,3 ^. 0,8+0,3 ^. 0,8= 0,84.

Ответ: Вероятность того, что взятое случайным образом изделие, будет качественным, равна 0,84.

Задание 1.3

В городе имеются N=3 оптовых баз. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна p=0,15. Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. Построить многоугольник распределения. Найти дисперсию и среднеквадратичное отклонение числа баз, на которых искомый товар отсутствует в данный момент.

Решение. Вычисления будем проводить по формуле Бернулли:

P_n(k) = C^k_n ^. p^{k .} q^n-k.

₀

^p₁^{= P(x=0) = P}₃ ^{(0) = C}₃ ^{. p0 . q3 = 1. 1. 0,853 = 0,614,}

₁

^p₂ ^{= P(x=1) = P}₃^{(1) = C}₃ ^{. p1 . q2 = 3. 0,15 . 0, 852 = 0,325,}

₂

^p₃ ^{= P(x=2) = P}₃^{(2) = C}₃ ^{. p2 . q1 = 3 . 0,152 . 0,85 = 0,0544,}

₃

^p₄ ^{= P(x=3) = P}₃^{(3) = C}₃ ^{. p3 . q0 = 1. 0,153 . 1 = 0,0034.}

^{Проверим: p}₁ ^{+ p}₂ ^{+ p}₃ ^{+ p}₄ ^{= 0,614 + 0,325 + 0,0574 + 0,0034 =1.}

^{Тогда закон распределения числа баз, на которых искомый товар отсутствует в данный момент, примет вид}

xi	0	1	2	3
pi	0,6140	0,3250	0,0574	0,0034

^{Вычислим математическое ожидание случайной величины Х и M(X2):}

^{M(X) = x}₁ ^{. p}₁ ^{+ x}₂ ^{. p}₂ ^{+ x}₃ ^{. p}₃ ^{+ x}₄ ^{. p}₄ ^{= 0 . 0,61 + 1 . 0,325 + 2 . 0,057 + +3 . 0,0034 = 0,325 + 0,114 + 0,0102 = 0,45,}

^{M(X2) = x}₁^{2. p}₁ ^{+ x}₂^{2 . p}₂ ^{+ x}₃^{2 . p}₃ ^{+ x}₄^{2 . p}₄ ^{= 0,325 + 4 . 0,057 + 9 . 0,0034= = 0,553 + 0,0306 = 0,58.}

^{Затем определим дисперсию по формуле}

^{D(X) = M(X2) - (M(X))2 = 0,58 – 0,2 = 0,38.}

^{Среднеквадратичное отклонение равно}

^{(X) = √ 0,38 = 0,62.}

^{Построим многоугольник распределения (рис.6)}

^0,6

^0,3

^0,1

^{0 1 2 3}

^Рис.6