МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ф едеральное агентство по образованию

Санкт-Петербургский государственный университет сервиса и экономики

Кафедра "Прикладная математика и эконометрика"

Б.В. Берсенадзе

С.И. Никитин

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания к

выполнению контрольных работ для студентов заочного отделения институтов ЭУПС, РЭУ, ТМиО, ТРБ, ЮФ.

Санкт-Петербург 2009

Требования к оформлению контрольных работ

1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических методов в экономике); название и номер контрольной работы; название (номер) специальности; фамилию, имя, отчество и личный шифр студента.

2. На каждой странице надо оставить поля размером 4 см для оценки решения задач и методических указаний проверяющего работу.

3. Условия задач переписывать полностью необязательно, достаточно указать номер задачи по данному сборнику. В условия задач надо сначала подставить конкретные числовые значения параметров т и п, и только после этого приступать к их решению.

4. Задачи в контрольной работе нужно располагать в порядке возрастания номеров.

Таблица 1 (выбор параметра т)

А	0	1	2	3	4	5	6	7	8	9
т	1	2	3	4	5	6	7	8	9	10

Таблица 2 (выбор параметра п )

В	0	1	2	3	4	5	6	7	8	9
п	5	3	2	4	1	4	5	2	3	1

Например, если шифр студента 1604 — 037, то А = 3, В = 7, и из таблиц находим, что т = 4, п = 2. Полученные т = 4 и п = 2 подставляются в условия всех задач контрольной работы этого студента.

12. Теория вероятностей.

1. Случайные события.

   1. В ящике находятся 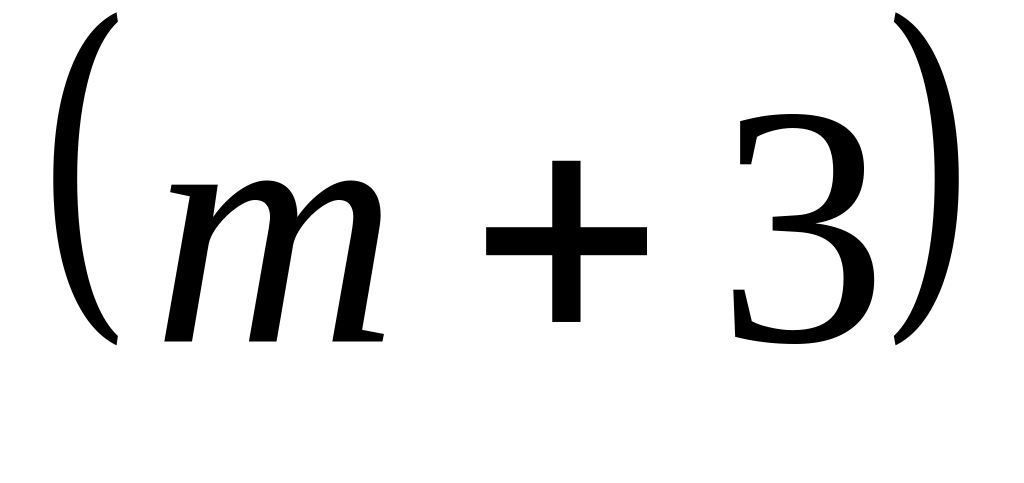одинаковых пар перчаток черного цвета и одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пару.

   2. В урне находятся три шара белого цвета и шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

а) ровно два белых шара; б) не менее двух белых шаров.

3. В урне находятся белых и черных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счету шар окажется белым.

2. Случайные величины.

1. Закон распределения дискретной случайной величины 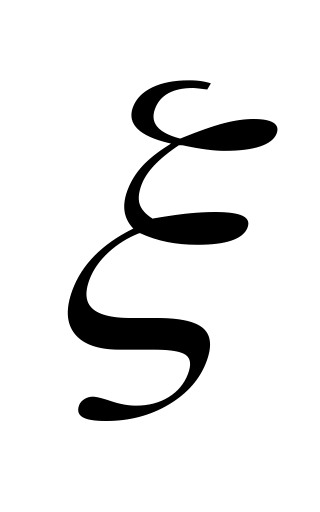имеет вид:

	-2	-1	0
	0,2	0,1	0,2

Найти вероятности , , и дисперсию , если математическое ожидание .

2. Плотность распределения непрерывной случайной величины имеет вид:

Найти:

а) параметр а; б) функцию распределения ;

в) вероятность попадания случайной величины в интервал

;

г) математическое ожидание и дисперсию .

Построить график функций и .

3. Случайные величины имеют геометрическое, биноминальное и пуассоновское распределения соответственно. Найти вероятности , если математическое ожидание , а дисперсия .

4. Случайные величины имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности , если у этих случайных величин математические ожидания и среднее квадратические отклонения равны m.

12. Математическая статистика.

1. Численная обработка данных одномерной выборки.

Выборка объемом изменений задана таблицей:

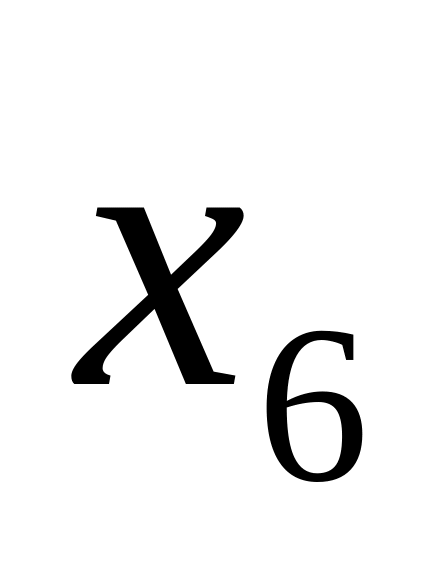
	5	13			19	10	3

где – результаты измерений, – частоты, с которыми встречаются значения , , .

1. Построить полигон относительных частот .

2. Вычислить среднее выборочное , выборочную дисперсию и среднее квадратическое отклонение .

3. По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости .

Примечание. Для расчетов и рекомендуется перейти к условным значениям и, взяв за ложный нуль значение с наибольшей частотой, использовать суммы и .