Практическая работа №4 определение потерь давления при течении промывочный жидкости в затрубном пространстве

Целью работы является определение потерь давления при течении промывочной жидкости в кольцевом зазоре между бурильной колонной и стенками скважины. Основные элементы (по протяженности) технологического инструмента – это утяжеленные и рабочие бурильные трубы. В результате изменения кольцевого зазора между стенками скважины и указанными элементами может измениться характер течения жидкости и методика расчета потерь давления. Местные потери, обусловленные наличием замков бурильных труб, при выполнении рассматриваемой работы не учитываются.

Исходные данные для выполнения работы:

• расход промывочной жидкости ;

• плотность промывочной жидкости ;

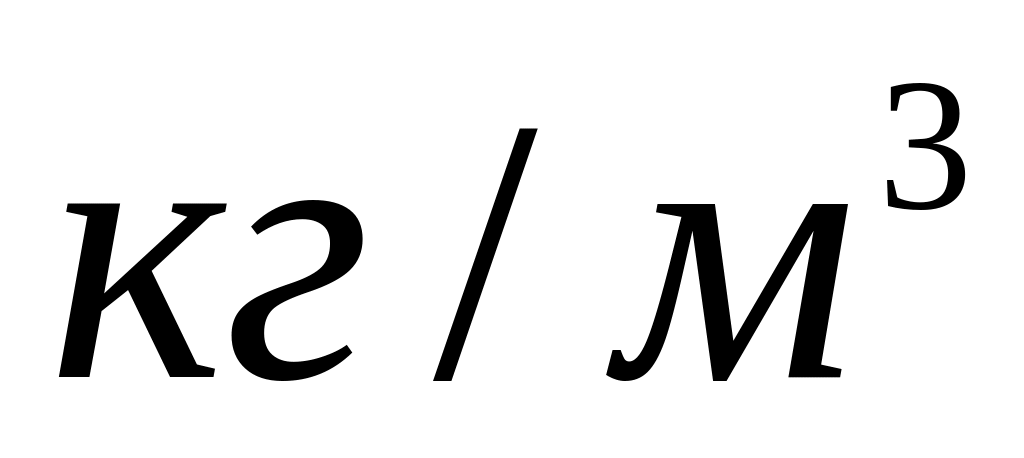• предельное напряжение сдвига раствора ;

• пластическая вязкость раствора ;

• общая длина бурильных труб, ;

• общая длина УБТ ,м;

• диаметр скважины ;

• диаметр наружный бурильных труб ;

• диаметр наружный УБТ .

Требуется определить потери давления при течении промывочной жидкости в кольцевом зазоре между диаметром скважины и УБТ и между диаметром скважины и бурильными трубами. Потерей давления на местных сопротивлениях (замки бурильной колонны) пренебречь.

Методика выполнения работы

Общие потери давления при течении в жидкости в кольцевом пространстве по аналогии с формулой (3.1) будут равны:

(4.1)

где -потери давления при течении раствора между стенками скважины и бурильными трубами;

- потери давления при течении раствора между стенками скважины и УБТ.

Определим режим течения жидкости в вышеуказанных кольцевых зазорах. С этой целью вычислим критические числа Рейнольдса и , которые по аналогии с формулой (3.2.) будут равны:

; (4.2 )

. (4.3 )

Затем определяются действительные числа Рейнольдса и при течении раствора в затрубном пространстве, которые определяются из следующих соотношений:

; (4.4 )

. (4.5 )

Если указанные действительные числа Рейнольдса больше соответствующих критических значений чисел. и , то режим течения раствора турбулентный, в противном случае течение происходит в ламинарном режиме.

При турбулентном режиме потери давления при течении жидкости в кольцевом пространстве рассчитываются по формуле Дарси-Вейсбаха.

; (4.6 )

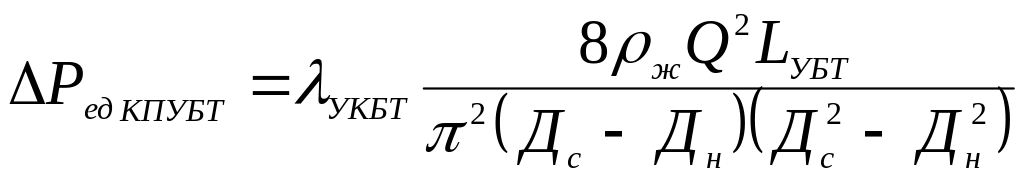, (4.7 )

где -коэффициенты гидравлических сопротивлений при течении раствора соответственно в кольцевым зазоре между скважиной и бурильными трубами и между скважиной и УБТ.

Значения указанных коэффициентов определяются по формулам:

(4.8 )

(4.9 )

R_e= v_m(D₂- D₁)ρ/η_ρ

Рисунок 4.1– Коэффициент гидравлического сопротивление при течении

бингамовской жидкости в кольцевом пространстве

где -шероховатость; для необсаженных участков затрубного пространства; .

При ламинарном течении для определения коэффициентов гидравлических сопротивлений первоначально устанавливаются критерии Бингама при течении жидкости в затрубном пространстве:

; (4.10)

. (4.11)

По вычисленным действительным числам Рейнольдса и и критерия Бингама и по графику (рисунок 4.1) определяем коэффициенты сопротивлений и . Для этого по оси абсцисс определяем точку, соответствующую величине (или ); из найденной точки восставляем перпендикуляр до пересечения с наклонной линий, соответствующей найденному значению. ( или ). Из полученной точки пересечения опускаем перпендикуляр на ось ординат. Точка пересечения с последней укажет искомые величины гидравлических сопротивлений. и . Затем по формулам (4.6) (4.7) определяются перепады давления и , а по формуле (4.1) –общий перепад давления .